6.4 다중공선성과 변수 선택#
다중공선성(multicollinearity)란 독립 변수의 일부가 다른 독립 변수의 조합으로 표현될 수 있는 경우이다. 독립 변수들이 서로 독립이 아니라 상호상관관계가 강한 경우에 발생한다. 이는 독립 변수의 공분산 행렬이 full rank 이어야 한다는 조건을 침해한다.
다음 데이터는 미국의 거시경제지표를 나타낸 것이다.
TOTEMP - Total Employment
GNPDEFL - GNP deflator
GNP - GNP
UNEMP - Number of unemployed
ARMED - Size of armed forces
POP - Population
YEAR - Year (1947 - 1962)
스캐터 플롯에서 보듯이 독립변수간의 상관관계가 강하다.
from statsmodels.datasets.longley import load_pandas
dfy = load_pandas().endog
dfX = load_pandas().exog
df = pd.concat([dfy, dfX], axis=1)
sns.pairplot(dfX)
plt.show()
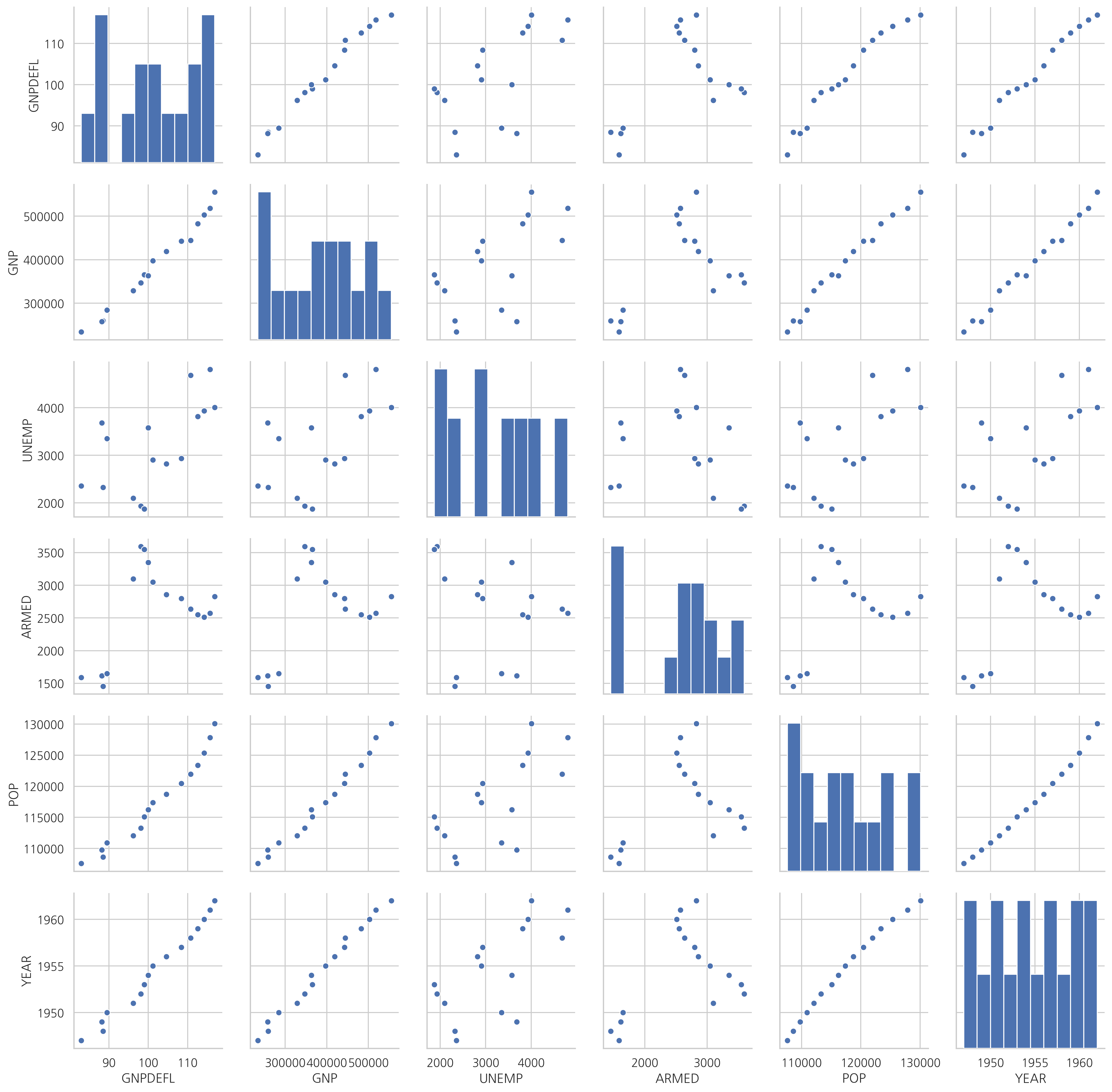
상관관계는 상관계수 행렬로도 살펴볼 수 있다.
dfX.corr()
| GNPDEFL | GNP | UNEMP | ARMED | POP | YEAR | |
|---|---|---|---|---|---|---|
| GNPDEFL | 1.000000 | 0.991589 | 0.620633 | 0.464744 | 0.979163 | 0.991149 |
| GNP | 0.991589 | 1.000000 | 0.604261 | 0.446437 | 0.991090 | 0.995273 |
| UNEMP | 0.620633 | 0.604261 | 1.000000 | -0.177421 | 0.686552 | 0.668257 |
| ARMED | 0.464744 | 0.446437 | -0.177421 | 1.000000 | 0.364416 | 0.417245 |
| POP | 0.979163 | 0.991090 | 0.686552 | 0.364416 | 1.000000 | 0.993953 |
| YEAR | 0.991149 | 0.995273 | 0.668257 | 0.417245 | 0.993953 | 1.000000 |
cmap = sns.light_palette("darkgray", as_cmap=True)
sns.heatmap(dfX.corr(), annot=True, cmap=cmap)
plt.show()
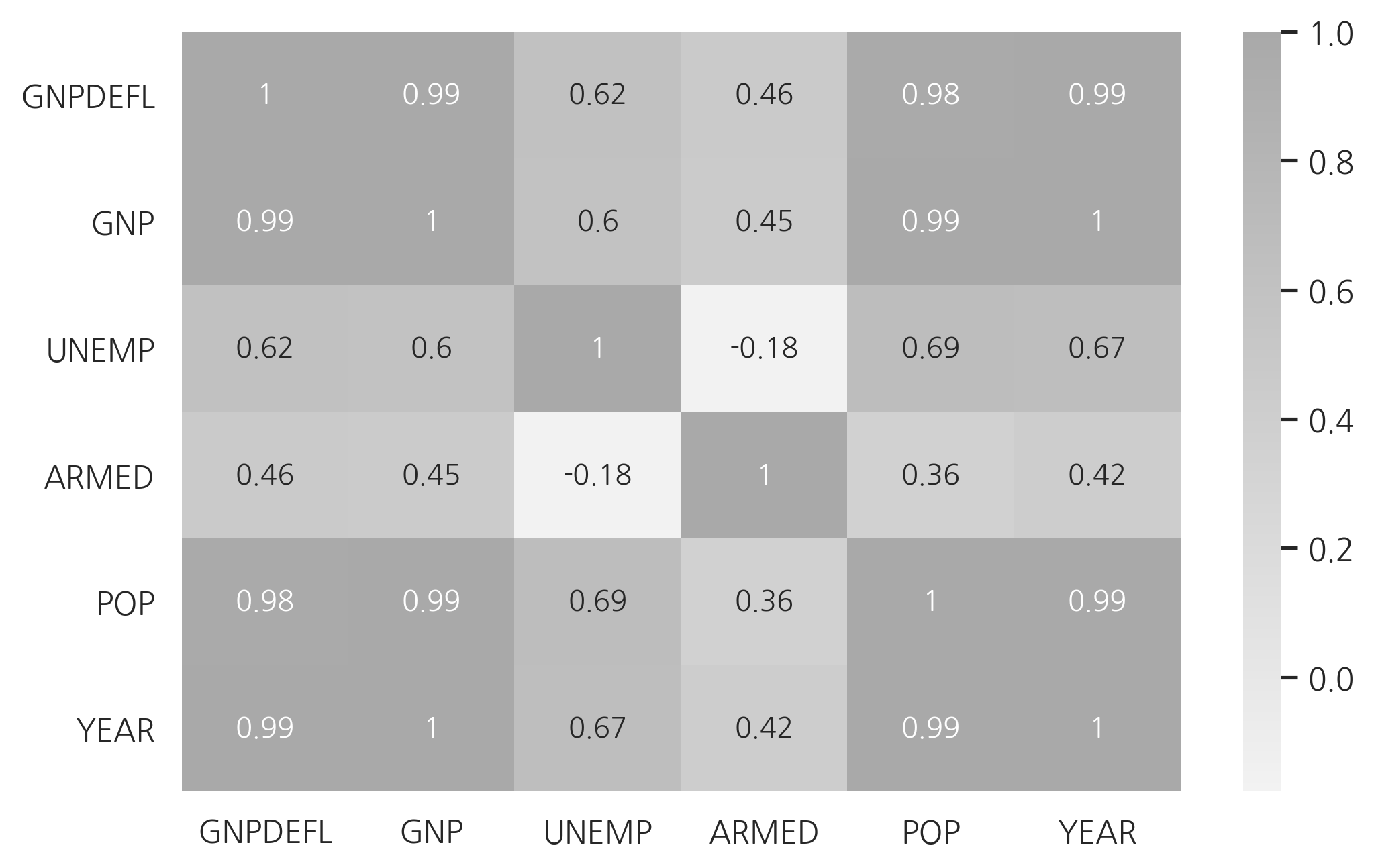
다중 공선성이 있으면 독립변수의 공분산 행렬의 조건수(conditional number)가 증가한다.
from sklearn.model_selection import train_test_split
def get_model1(seed):
df_train, df_test = train_test_split(df, test_size=0.5, random_state=seed)
model = sm.OLS.from_formula("TOTEMP ~ GNPDEFL + POP + GNP + YEAR + ARMED + UNEMP", data=df_train)
return df_train, df_test, model.fit()
df_train, df_test, result1 = get_model1(3)
print(result1.summary())
OLS Regression Results
==============================================================================
Dep. Variable: TOTEMP R-squared: 1.000
Model: OLS Adj. R-squared: 0.997
Method: Least Squares F-statistic: 437.5
Date: Sun, 23 Jun 2019 Prob (F-statistic): 0.0366
Time: 18:13:38 Log-Likelihood: -44.199
No. Observations: 8 AIC: 102.4
Df Residuals: 1 BIC: 103.0
Df Model: 6
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -1.235e+07 2.97e+06 -4.165 0.150 -5e+07 2.53e+07
GNPDEFL 106.2620 75.709 1.404 0.394 -855.708 1068.232
POP 2.2959 0.725 3.167 0.195 -6.915 11.506
GNP -0.3997 0.120 -3.339 0.185 -1.920 1.121
YEAR 6300.6231 1498.900 4.203 0.149 -1.27e+04 2.53e+04
ARMED -0.2450 0.402 -0.609 0.652 -5.354 4.864
UNEMP -6.3311 1.324 -4.782 0.131 -23.153 10.491
==============================================================================
Omnibus: 0.258 Durbin-Watson: 1.713
Prob(Omnibus): 0.879 Jarque-Bera (JB): 0.304
Skew: 0.300 Prob(JB): 0.859
Kurtosis: 2.258 Cond. No. 2.01e+10
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.01e+10. This might indicate that there are
strong multicollinearity or other numerical problems.
또한 다음처럼 학습용 데이터와 검증용 데이터로 나누어 회귀분석 성능을 비교하면 과최적화가 발생하였음을 알 수 있다.
def calc_r2(df_test, result):
target = df.loc[df_test.index].TOTEMP
predict_test = result.predict(df_test)
RSS = ((predict_test - target)**2).sum()
TSS = ((target - target.mean())**2).sum()
return 1 - RSS / TSS
test1 = []
for i in range(10):
df_train, df_test, result = get_model1(i)
test1.append(calc_r2(df_test, result))
test1
[0.9815050656837723,
0.9738497543069347,
0.9879366369871746,
0.7588861967897188,
0.980720608930437,
0.8937889315168234,
0.8798563810651999,
0.9314665778963799,
0.8608525682180641,
0.9677198735170137]
독립변수가 서로 의존하게 되면 이렇게 과최적화(over-fitting) 문제가 발생하여 회귀 결과의 안정성을 해칠 가능성이 높아진다. 이를 방지하는 방법들은 다음과 같다.
변수 선택법으로 의존적인 변수 삭제
PCA(principal component analysis) 방법으로 의존적인 성분 삭제
정규화(regularized) 방법 사용
VIF#
다중 공선성을 없애는 가장 기본적인 방법은 다른 독립변수에 의존하는 변수를 없애는 것이다. 가장 의존적인 독립변수를 선택하는 방법으로는 VIF(Variance Inflation Factor)를 사용할 수 있다. VIF는 독립변수를 다른 독립변수로 선형회귀한 성능을 나타낸 것이다. \(i\)번째 변수의 VIF는 다음과 같이 계산한다.
여기에서 \(R^2_i\)는 다른 변수로 \(i\)번째 변수를 선형회귀한 성능(결정 계수)이다. 다른 변수에 의존적일 수록 VIF가 커진다.
StatsModels에서는 variance_inflation_factor 명령으로 VIF를 계산한다.
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(
dfX.values, i) for i in range(dfX.shape[1])]
vif["features"] = dfX.columns
vif
| VIF Factor | features | |
|---|---|---|
| 0 | 12425.514335 | GNPDEFL |
| 1 | 10290.435437 | GNP |
| 2 | 136.224354 | UNEMP |
| 3 | 39.983386 | ARMED |
| 4 | 101193.161993 | POP |
| 5 | 84709.950443 | YEAR |
상관계수와 VIF를 사용하여 독립 변수를 선택하면 GNP, ARMED, UNEMP 세가지 변수만으로도 비슷한 수준의 성능이 나온다는 것을 알 수 있다.
def get_model2(seed):
df_train, df_test = train_test_split(df, test_size=0.5, random_state=seed)
model = sm.OLS.from_formula("TOTEMP ~ scale(GNP) + scale(ARMED) + scale(UNEMP)", data=df_train)
return df_train, df_test, model.fit()
df_train, df_test, result2 = get_model2(3)
print(result2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: TOTEMP R-squared: 0.989
Model: OLS Adj. R-squared: 0.981
Method: Least Squares F-statistic: 118.6
Date: Sun, 23 Jun 2019 Prob (F-statistic): 0.000231
Time: 18:13:39 Log-Likelihood: -57.695
No. Observations: 8 AIC: 123.4
Df Residuals: 4 BIC: 123.7
Df Model: 3
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
Intercept 6.538e+04 163.988 398.686 0.000 6.49e+04 6.58e+04
scale(GNP) 4338.7051 406.683 10.669 0.000 3209.571 5467.839
scale(ARMED) -812.1407 315.538 -2.574 0.062 -1688.215 63.933
scale(UNEMP) -1373.0426 349.316 -3.931 0.017 -2342.898 -403.187
==============================================================================
Omnibus: 0.628 Durbin-Watson: 2.032
Prob(Omnibus): 0.731 Jarque-Bera (JB): 0.565
Skew: 0.390 Prob(JB): 0.754
Kurtosis: 1.958 Cond. No. 4.77
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
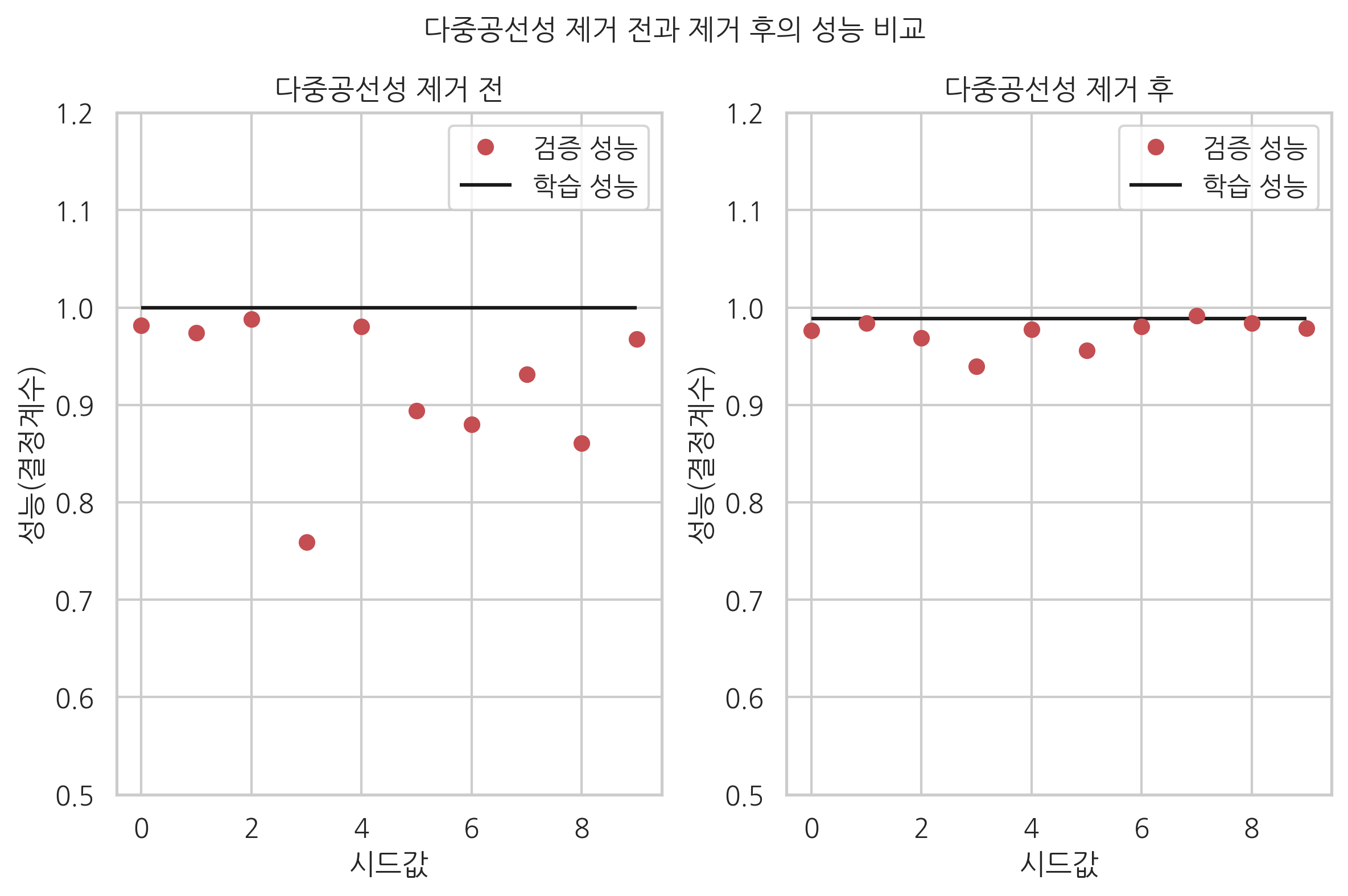
다중공선성을 제거한 경우에는 학습 성능과 검증 성능간의 차이가 줄어들었음을 확인할 수 있다. 즉, 과최적화가 발생하지 않는다.
test2 = []
for i in range(10):
df_train, df_test, result = get_model2(i)
test2.append(calc_r2(df_test, result))
test2
[0.9763608388904907,
0.9841984331185702,
0.9687069366140136,
0.9397304053201785,
0.9773357061188462,
0.9561262155732316,
0.980385249669863,
0.9917361722470804,
0.9837134067639467,
0.9789512977093212]
plt.subplot(121)
plt.plot(test1, 'ro', label="검증 성능")
plt.hlines(result1.rsquared, 0, 9, label="학습 성능")
plt.legend()
plt.xlabel("시드값")
plt.ylabel("성능(결정계수)")
plt.title("다중공선성 제거 전")
plt.ylim(0.5, 1.2)
plt.subplot(122)
plt.plot(test2, 'ro', label="검증 성능")
plt.hlines(result2.rsquared, 0, 9, label="학습 성능")
plt.legend()
plt.xlabel("시드값")
plt.ylabel("성능(결정계수)")
plt.title("다중공선성 제거 후")
plt.ylim(0.5, 1.2)
plt.suptitle("다중공선성 제거 전과 제거 후의 성능 비교", y=1.04)
plt.tight_layout()
plt.show()
보스턴 집값 예측 문제에 응용#
from sklearn.datasets import load_boston
boston = load_boston()
dfX0 = pd.DataFrame(boston.data, columns=boston.feature_names)
from patsy import dmatrix
formula = "scale(CRIM) + scale(I(CRIM ** 2)) + " + \
"scale(ZN) + scale(I(ZN ** 2)) + scale(INDUS) + " + \
"scale(NOX) + scale(RM) + scale(AGE) + " + \
"scale(np.log(DIS)) + scale(RAD) + scale(TAX) + " + \
"scale(np.log(PTRATIO)) + scale(B) + scale(np.log(LSTAT)) + CHAS"
dfX = dmatrix(formula, dfX0, return_type="dataframe")
dfy = pd.DataFrame(boston.target, columns=["MEDV"])
idx_outlier = \
np.array([7, 54, 148, 152, 160, 214, 253, 267, 364, 365, 367, 368, 369,
371, 372, 374, 380, 385, 397, 398, 399, 400, 401, 405, 409, 410,
412, 413, 414, 415, 416, 418, 419, 426, 445, 489, 490, 492, 505,
161, 162, 163, 166, 186, 195, 204, 225, 257, 267, 283, 368, 369,
370, 371, 372])
idx = list(set(range(len(dfX))).difference(idx_outlier))
dfX = dfX.iloc[idx, :].reset_index(drop=True)
dfy = dfy.iloc[idx, :].reset_index(drop=True)
cmap = sns.light_palette("black", as_cmap=True)
sns.heatmap(dfX.corr(), annot=True, fmt='3.1f', cmap=cmap)
plt.show()

vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(
dfX.values, i) for i in range(dfX.shape[1])]
vif["features"] = dfX.columns
vif = vif.sort_values("VIF Factor").reset_index(drop=True)
vif
| VIF Factor | features | |
|---|---|---|
| 0 | 1.061624 | CHAS |
| 1 | 1.338325 | scale(B) |
| 2 | 1.478553 | Intercept |
| 3 | 1.780320 | scale(np.log(PTRATIO)) |
| 4 | 2.596496 | scale(RM) |
| 5 | 3.748931 | scale(AGE) |
| 6 | 3.807459 | scale(INDUS) |
| 7 | 4.682812 | scale(np.log(LSTAT)) |
| 8 | 5.071802 | scale(NOX) |
| 9 | 5.215025 | scale(np.log(DIS)) |
| 10 | 9.107858 | scale(TAX) |
| 11 | 10.218588 | scale(I(CRIM ** 2)) |
| 12 | 11.254736 | scale(RAD) |
| 13 | 11.751869 | scale(I(ZN ** 2)) |
| 14 | 14.646056 | scale(ZN) |
| 15 | 21.260182 | scale(CRIM) |
model_boston1 = sm.OLS(np.log(dfy), dfX)
result_boston1 = model_boston1.fit()
print(result_boston1.summary())
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.872
Model: OLS Adj. R-squared: 0.868
Method: Least Squares F-statistic: 199.9
Date: Sun, 23 Jun 2019 Prob (F-statistic): 1.56e-185
Time: 18:13:41 Log-Likelihood: 317.45
No. Observations: 456 AIC: -602.9
Df Residuals: 440 BIC: -536.9
Df Model: 15
Covariance Type: nonrobust
==========================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------------
Intercept 3.0338 0.007 433.880 0.000 3.020 3.048
scale(CRIM) -0.3471 0.044 -7.976 0.000 -0.433 -0.262
scale(I(CRIM ** 2)) 0.3075 0.071 4.331 0.000 0.168 0.447
scale(ZN) -0.0465 0.022 -2.110 0.035 -0.090 -0.003
scale(I(ZN ** 2)) 0.0440 0.020 2.206 0.028 0.005 0.083
scale(INDUS) 0.0037 0.012 0.323 0.747 -0.019 0.026
scale(NOX) -0.0652 0.013 -5.001 0.000 -0.091 -0.040
scale(RM) 0.0999 0.011 9.195 0.000 0.079 0.121
scale(AGE) -0.0273 0.011 -2.438 0.015 -0.049 -0.005
scale(np.log(DIS)) -0.1008 0.014 -7.368 0.000 -0.128 -0.074
scale(RAD) 0.1634 0.020 8.106 0.000 0.124 0.203
scale(TAX) -0.0934 0.018 -5.153 0.000 -0.129 -0.058
scale(np.log(PTRATIO)) -0.0699 0.008 -8.872 0.000 -0.085 -0.054
scale(B) 0.0492 0.007 6.699 0.000 0.035 0.064
scale(np.log(LSTAT)) -0.1487 0.013 -11.074 0.000 -0.175 -0.122
CHAS 0.0659 0.026 2.580 0.010 0.016 0.116
==============================================================================
Omnibus: 28.653 Durbin-Watson: 1.309
Prob(Omnibus): 0.000 Jarque-Bera (JB): 43.266
Skew: 0.465 Prob(JB): 4.03e-10
Kurtosis: 4.188 Cond. No. 35.2
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
cols = ["Intercept", "CHAS", "scale(B)", "scale(CRIM)",
"scale(np.log(PTRATIO))", "scale(RM)", "scale(np.log(LSTAT))"]
model_boston2 = sm.OLS(np.log(dfy), dfX[cols])
result_boston2 = model_boston2.fit()
print(result_boston2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.836
Model: OLS Adj. R-squared: 0.834
Method: Least Squares F-statistic: 380.7
Date: Sun, 23 Jun 2019 Prob (F-statistic): 1.42e-172
Time: 18:13:41 Log-Likelihood: 260.52
No. Observations: 456 AIC: -507.0
Df Residuals: 449 BIC: -478.2
Df Model: 6
Covariance Type: nonrobust
==========================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------------
Intercept 3.0192 0.007 445.252 0.000 3.006 3.033
CHAS 0.0884 0.028 3.141 0.002 0.033 0.144
scale(B) 0.0558 0.008 6.989 0.000 0.040 0.072
scale(CRIM) -0.1179 0.013 -9.120 0.000 -0.143 -0.092
scale(np.log(PTRATIO)) -0.0508 0.007 -6.936 0.000 -0.065 -0.036
scale(RM) 0.1153 0.011 10.828 0.000 0.094 0.136
scale(np.log(LSTAT)) -0.1570 0.011 -14.179 0.000 -0.179 -0.135
==============================================================================
Omnibus: 29.141 Durbin-Watson: 1.113
Prob(Omnibus): 0.000 Jarque-Bera (JB): 42.637
Skew: 0.483 Prob(JB): 5.51e-10
Kurtosis: 4.145 Cond. No. 5.91
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.