3.4 특잇값 분해¶
정방행렬은 고유분해로 고윳값과 고유벡터를 찾을 수 있었다. 정방행렬이 아닌 행렬은 고유분해가 불가능하다. 하지만 대신 고유분해와 비슷한 특이분해를 할 수 있다.
특잇값과 특이벡터¶
\(N \times M\) 크기의 행렬 \(A\)를 다음과 같은 3개의 행렬의 곱으로 나타내는 것을 특이분해(singular-decomposition) 또는 **특잇값 분해(singular value decomposition)**라고 한다.
\[
\begin{align}
A = U\Sigma V^T
\tag{3.4.1}
\end{align}
\]
여기에서 \(U, \Sigma, V\)는 다음 조건을 만족해야 한다.
대각성분이 양수인 대각행렬이어야 한다. 큰 수부터 작은 수 순서로 배열한다.
\[
\begin{align}
\Sigma \in \mathbf{R}^{N \times M}
\tag{3.4.2}
\end{align}
\]
\(U\)는 \(N\)차원 정방행렬로 모든 열벡터가 단위벡터이고 서로 직교해야 한다.
\[
\begin{align}
U \in \mathbf{R}^{N \times N}
\tag{3.4.3}
\end{align}
\]
\(V\)는 \(M\)차원 정방행렬로 모든 열벡터가 단위벡터이고 서로 직교해야 한다.
\[
\begin{align}
V \in \mathbf{R}^{M \times M}
\tag{3.4.4}
\end{align}
\]
위 조건을 만족하는 행렬 \(\Sigma\)의 대각성분들을 특잇값(singular value), 행렬 \(U\)의 열벡터들을 왼쪽 특이벡터(left singular vector), 행렬 \(V\)의 행벡터들을 오른쪽 특이벡터(right singular vector)라고 부른다.
[정리] 특이분해는 모든 행렬에 대해 가능하다. 즉 어떤 행렬이 주어지더라도 위와 같이 특이분해할 수 있다.
증명은 이 책의 범위를 벗어나므로 생략한다.
특이값 분해 행렬의 크기¶
특잇값의 개수는 행렬의 열과 행의 개수 중 작은 값과 같다. 특이분해된 형태를 구체적으로 쓰면 다음과 같다.
만약 \(N > M\)이면 \(\Sigma\) 행렬이 \(M\)개의 특잇값(대각성분)을 가지고 다음처럼 아랫 부분이 영행렬이 된다.
\[\begin{split}
\begin{align}
A =
\begin{bmatrix}
\boxed{\begin{matrix} \\ \\ \\ \\ \\ \, u_1 \, \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\boxed{\begin{matrix} \\ \\ \\ \\ \\ \, u_2 \, \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\boxed{\begin{matrix} \\ \\ \\ \\ \\ \, u_3 \, \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\cdots \!\!\!\!&
\boxed{\begin{matrix} \\ \\ \\ \\ \\ u_M \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\cdots \!\!\!\!&
\boxed{\begin{matrix} \\ \\ \\ \\ \\ u_N \\ \\ \\ \\ \\ \\ \end{matrix}}
\end{bmatrix}
\begin{bmatrix}
\boxed{\sigma_1 \phantom{\dfrac{}{}} \!\!} & 0 & 0 & \cdots & 0 \\
0 & \boxed{\sigma_2 \phantom{\dfrac{}{}} \!\!} & 0 & \cdots & 0 \\
0 & 0 & \boxed{\sigma_3 \phantom{\dfrac{}{}} \!\!} & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots \\
0 & 0 & 0 & \cdots & \boxed{\sigma_M \phantom{\dfrac{}{}} \!\!} \\
0 & 0 & 0 & \cdots & 0 \\
\vdots & \vdots & \vdots & & \vdots \\
0 & 0 & 0 & \cdots & 0 \\
\end{bmatrix}
\begin{bmatrix}
\boxed{\begin{matrix} & & & v_1^T & & & \end{matrix}} \\
\boxed{\begin{matrix} & & & v_2^T & & & \end{matrix}} \\
\vdots \\
\boxed{\begin{matrix} & & & v_M^T & & & \end{matrix}} \\
\end{bmatrix}
\tag{3.4.5}
\end{align}
\end{split}\]
반대로 \(N < M\)이면 \(\Sigma\) 행렬이 \(N\)개의 특잇값(대각성분)을 가지고 다음처럼 오른쪽 부분이 영행렬이 된다.
\[\begin{split}
\begin{align}
A =
\begin{bmatrix}
\boxed{\begin{matrix} \\ \\ \\ \, u_1 \, \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\boxed{\begin{matrix} \\ \\ \\ \, u_2 \, \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\cdots \!\!\!\!&
\boxed{\begin{matrix} \\ \\ \\ u_N \\ \\ \\ \\ \end{matrix}}
\end{bmatrix}
\begin{bmatrix}
\boxed{\sigma_1 \phantom{\dfrac{}{}} \!\!} & 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\
0 & \boxed{\sigma_2 \phantom{\dfrac{}{}} \!\!} & 0 & \cdots & 0 & 0 & \cdots & 0 \\
0 & 0 & \boxed{\sigma_3 \phantom{\dfrac{}{}} \!\!} & \cdots & 0 & 0 & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & & \vdots \\
0 & 0 & 0 & \cdots & \boxed{\sigma_N \phantom{\dfrac{}{}} \!\!} & 0 & \cdots & 0 \\
\end{bmatrix}
\begin{bmatrix}
\boxed{\begin{matrix} \quad & \quad & \quad & v_1^T & \quad & \quad & \quad \end{matrix}} \\
\boxed{\begin{matrix} \quad & \quad & \quad & v_2^T & \quad & \quad & \quad \end{matrix}} \\
\boxed{\begin{matrix} \quad & \quad & \quad & v_3^T & \quad & \quad & \quad \end{matrix}} \\
\vdots \\
\boxed{\begin{matrix} \quad & \quad & \quad & v_N^T & \quad & \quad & \quad \end{matrix}} \\
\vdots \\
\boxed{\begin{matrix} \quad & \quad & \quad & v_M^T & \quad & \quad & \quad \end{matrix}} \\
\end{bmatrix}
\tag{3.4.6}
\end{align}
\end{split}\]
행렬의 크기만 표시하면 다음과 같다.
\[\begin{split}
\begin{align}
N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \\ \\ \end{matrix}}\right.\!\!
\overbrace{
\boxed{
\begin{matrix}
\; & & \; \\
\; & & \; \\
\; & A & \; \\
\; & & \; \\
\; & & \; \\
\end{matrix}
}}^{\large M}
=
N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \\ \\ \end{matrix}}\right.\!\!
\overbrace{
\boxed{
\begin{matrix}
\; & & & & \quad \\
\; & & & & \quad \\
\; & & \; U & & \quad \\
\; & & & & \quad \\
\; & & & & \quad \\
\end{matrix}
}}^{\large N}
\;
\overbrace{
\boxed{
\begin{matrix}
& & \\
& & \\
& \Sigma & \\
& & \\
& & \\
\end{matrix}
}}^{\large M}
\;
\overbrace{
\boxed{
\begin{matrix}
\; & & \; \\
\; & V^T & \; \\
\; & & \; \\
\end{matrix}
}}^{\large M}
\!\!\left.\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right\}M
\tag{3.4.7}
\end{align}
\end{split}\]
또는
\[\begin{split}
\begin{align}
N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right.\!\!
\overbrace{
\boxed{
\begin{matrix}
\quad & & & & \quad \\
\quad & & A & & \quad \\
\quad & & & & \quad \\
\end{matrix}
}}^{\large M}
=
N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right.\!\!
\overbrace{
\boxed{
\begin{matrix}
\begin{matrix}
\, & & \; \\
\, & U \; \\
\, & & \; \\
\end{matrix}
\end{matrix}
}}^{\large N}
\;
\overbrace{
\boxed{
\begin{matrix}
\quad & & & & \quad \\
\quad & & \Sigma & & \quad \\
\quad & & & & \quad \\
\end{matrix}
}}^{\large M}
\;
\overbrace{
\boxed{
\begin{matrix}
\; & & & & \quad \\
\; & & & & \quad \\
\; & & \; V^T & & \quad \\
\; & & & & \quad \\
\; & & & & \quad \\
\end{matrix}
}}^{\large M}
\!\!\left.\phantom{\begin{matrix} \\ \\ \\\\ \\ \end{matrix}}\right\}M
\tag{3.4.8}
\end{align}
\end{split}\]
예제¶
행렬 \(A\)
\[\begin{split}
\begin{align}
A =
\begin{bmatrix}
3 & -1 \\
1 & 3 \\
1 & 1
\end{bmatrix}
\tag{3.4.9}
\end{align}
\end{split}\]
는 다음처럼 특이분해할 수 있다.
\[\begin{split}
\begin{align}
A =
\begin{bmatrix}
-\frac{1}{\sqrt{6}} & \frac{2}{\sqrt{5}} & -\frac{1}{\sqrt{6}} \\
-\frac{2}{\sqrt{6}} & -\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{30}} \\
-\frac{1}{\sqrt{6}} & 0 & \frac{5}{\sqrt{30}}
\end{bmatrix}
\begin{bmatrix}
\sqrt{12} & 0 \\
0 & \sqrt{10} \\
0 & 0
\end{bmatrix}
\begin{bmatrix}
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix}
\tag{3.4.10}
\end{align}
\end{split}\]
특잇값 분해의 축소형¶
특잇값 대각행렬에서 0인 부분은 사실상 아무런 의미가 없기 때문에 대각행렬의 0 원소 부분과 이에 대응하는 왼쪽(혹은 오른쪽) 특이벡터들을 없애고 다음처럼 축소된 형태로 해도 마찬가지로 원래 행렬이 나온다.
\(N\)이 \(M\)보다 큰 경우에는 왼쪽 특이벡터 중에서 \(u_{M+1}, \cdots, u_N\)을 없앤다.
\[\begin{split}
\begin{align}
A =
\begin{bmatrix}
\boxed{\begin{matrix} \\ \\ \\ \\ \\ \, u_1 \, \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\boxed{\begin{matrix} \\ \\ \\ \\ \\ \, u_2 \, \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\cdots \!\!\!\!&
\boxed{\begin{matrix} \\ \\ \\ \\ \\ u_M \\ \\ \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\end{bmatrix}
\begin{bmatrix}
\boxed{\sigma_1 \phantom{\dfrac{}{}} \!\!} & 0 & 0 & \cdots & 0 \\
0 & \boxed{\sigma_2 \phantom{\dfrac{}{}} \!\!} & 0 & \cdots & 0 \\
0 & 0 & \boxed{\sigma_3 \phantom{\dfrac{}{}} \!\!} & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots \\
0 & 0 & 0 & \cdots & \boxed{\sigma_M \phantom{\dfrac{}{}} \!\!} \\
\end{bmatrix}
\begin{bmatrix}
\boxed{\begin{matrix} & & & v_1^T & & & \end{matrix}} \\
\boxed{\begin{matrix} & & & v_2^T & & & \end{matrix}} \\
\vdots \\
\boxed{\begin{matrix} & & & v_M^T & & & \end{matrix}} \\
\end{bmatrix}
\tag{3.4.11}
\end{align}
\end{split}\]
\(N\)이 \(M\)보다 작은 경우에는 오른쪽 특이벡터 중에서 \(v_{N+1}, \cdots, v_M\)을 없앤다.
\[\begin{split}
\begin{align}
A =
\begin{bmatrix}
\boxed{\begin{matrix} \\ \\ \\ \, u_1 \, \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\boxed{\begin{matrix} \\ \\ \\ \, u_2 \, \\ \\ \\ \\ \end{matrix}} \!\!\!\!&
\cdots \!\!\!\!&
\boxed{\begin{matrix} \\ \\ \\ u_N \\ \\ \\ \\ \end{matrix}}
\end{bmatrix}
\begin{bmatrix}
\boxed{\sigma_1 \phantom{\dfrac{}{}} \!\!} & 0 & 0 & \cdots & 0 \\
0 & \boxed{\sigma_2 \phantom{\dfrac{}{}} \!\!} & 0 & \cdots & 0 \\
0 & 0 & \boxed{\sigma_3 \phantom{\dfrac{}{}} \!\!} & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \cdots & \boxed{\sigma_N \phantom{\dfrac{}{}} \!\!} \\
\end{bmatrix}
\begin{bmatrix}
\boxed{\begin{matrix} \quad & \quad & \quad & v_1^T & \quad & \quad & \quad \end{matrix}} \\
\boxed{\begin{matrix} \quad & \quad & \quad & v_2^T & \quad & \quad & \quad \end{matrix}} \\
\vdots \\
\boxed{\begin{matrix} \quad & \quad & \quad & v_N^T & \quad & \quad & \quad \end{matrix}} \\
\end{bmatrix}
\tag{3.4.12}
\end{align}
\end{split}\]
축소형의 경우에도 행렬의 크기만 표시하면 다음과 같다.
\[\begin{split}
\begin{align}
N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \\ \\ \end{matrix}}\right.\!\!
\overbrace{
\boxed{
\begin{matrix}
\; & & \; \\
\; & & \; \\
\; & A & \; \\
\; & & \; \\
\; & & \; \\
\end{matrix}
}}^{\large M}
=
N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \\ \\ \end{matrix}}\right.\!\!
\overbrace{
\boxed{
\begin{matrix}
& & \\
& & \\
& U & \\
& & \\
& & \\
\end{matrix}
}}^{\large M}
\;
\overbrace{
\boxed{
\begin{matrix}
\; & & \; \\
\; & \Sigma & \; \\
\; & & \; \\
\end{matrix}
}}^{\large M}
\;
\overbrace{
\boxed{
\begin{matrix}
\; & & \; \\
\; & V^T & \; \\
\; & & \; \\
\end{matrix}
}}^{\large M}
\!\!\left.\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right\}M
\tag{3.4.13}
\end{align}
\end{split}\]
또는
\[\begin{split}
\begin{align}
N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right.\!\!
\overbrace{
\boxed{
\begin{matrix}
\quad & & & & \quad \\
\quad & & A & & \quad \\
\quad & & & & \quad \\
\end{matrix}
}}^{\large M}
=
N\;\left\{\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right.\!\!
\overbrace{
\boxed{
\begin{matrix}
\begin{matrix}
\, & & \; \\
\, & U \; \\
\, & & \; \\
\end{matrix}
\end{matrix}
}}^{\large N}
\;
\overbrace{
\boxed{
\begin{matrix}
\, & & \; \\
\, & \Sigma \; \\
\, & & \; \\
\end{matrix}
}}^{\large N}
\;
\overbrace{
\boxed{
\begin{matrix}
\quad & & & & \quad \\
\quad & & V^T & & \quad \\
\quad & & & & \quad \\
\end{matrix}
}}^{\large M}
\!\!\left.\phantom{\begin{matrix} \\ \\ \\ \end{matrix}}\right\}N
\tag{3.4.14}
\end{align}
\end{split}\]
예제¶
행렬 \(A\)
\[\begin{split}
\begin{align}
A =
\begin{bmatrix}
3 & -1 \\
1 & 3 \\
1 & 1
\end{bmatrix}
\tag{3.4.15}
\end{align}
\end{split}\]
의 특이분해 축소형은 다음과 같다.
\[\begin{split}
\begin{align}
A =
\begin{bmatrix}
-\frac{1}{\sqrt{6}} & \frac{2}{\sqrt{5}} \\
-\frac{2}{\sqrt{6}} & -\frac{1}{\sqrt{5}} \\
-\frac{1}{\sqrt{6}} & 0
\end{bmatrix}
\begin{bmatrix}
\sqrt{12} & 0 \\
0 & \sqrt{10} \\
\end{bmatrix}
\begin{bmatrix}
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix}
\tag{3.4.16}
\end{align}
\end{split}\]
파이썬을 사용한 특이분해¶
numpy.linalg 서브패키지와 scipy.linalg 서브패키지에서는 특이분해를 할 수 있는 svd() 명령을 제공한다. 오른쪽 특이행렬은 전치행렬로 출력된다는 점에 주의하라.
from numpy.linalg import svd
A = np.array([[3, -1], [1, 3], [1, 1]])
U, S, VT = svd(A)
U
array([[-4.08248290e-01, 8.94427191e-01, -1.82574186e-01],
[-8.16496581e-01, -4.47213595e-01, -3.65148372e-01],
[-4.08248290e-01, -2.06937879e-16, 9.12870929e-01]])
S
array([3.46410162, 3.16227766])
np.diag(S, 1)[:, 1:]
array([[3.46410162, 0. ],
[0. , 3.16227766],
[0. , 0. ]])
VT
array([[-0.70710678, -0.70710678],
[ 0.70710678, -0.70710678]])
U @ np.diag(S, 1)[:, 1:] @ VT
array([[ 3., -1.],
[ 1., 3.],
[ 1., 1.]])
축소형을 구하려면 인수 full_matrices=False로 지정한다.
U2, S2, VT2 = svd(A, full_matrices=False)
U2
array([[-4.08248290e-01, 8.94427191e-01],
[-8.16496581e-01, -4.47213595e-01],
[-4.08248290e-01, -2.06937879e-16]])
S2
array([3.46410162, 3.16227766])
VT2
array([[-0.70710678, -0.70710678],
[ 0.70710678, -0.70710678]])
U2 @ np.diag(S2) @ VT2
array([[ 3., -1.],
[ 1., 3.],
[ 1., 1.]])
연습 문제 3.4.1¶
NumPy를 사용하여 다음 행렬을 특잇값 분해를 한다(축소형이 아닌 방법과 축소형 방법을 각각 사용한다). 또한 다시 곱해서 원래의 행렬이 나오는 것을 보여라.
\[\begin{split}
\begin{align}
B =
\begin{bmatrix}
3 & 2 & 2 \\
2 & 3 & -2
\end{bmatrix}
\tag{3.4.17}
\end{align}
\end{split}\]
\[\begin{split}
\begin{align}
C =
\begin{bmatrix}
2 & 4 \\
1 & 3 \\
0 & 0 \\
0 & 0 \\
\end{bmatrix}
\tag{3.4.18}
\end{align}
\end{split}\]
특잇값과 특이벡터의 관계¶
행렬 \(V\)는 정규직교(orthonormal)행렬이므로 전치행렬이 역행렬이다.
\[
\begin{align}
V^T = V^{-1}
\tag{3.4.19}
\end{align}
\]
특이분해된 등식의 양변에 \(V\)를 곱하면,
\[
\begin{align}
AV = U\Sigma V^TV = U\Sigma
\tag{3.4.20}
\end{align}
\]
\[\begin{split}
\begin{align}
A
\begin{bmatrix}
v_1 & v_2 & \cdots & v_M
\end{bmatrix}
=
\begin{bmatrix}
u_1 & u_2 & \cdots & u_N
\end{bmatrix}
\begin{bmatrix}
\sigma_1 & 0 & \cdots \\
0 & \sigma_2 & \cdots \\
\vdots & \vdots & \ddots \\
\end{bmatrix}
\tag{3.4.21}
\end{align}
\end{split}\]
행렬 \(A\)를 곱하여 정리하면 \(M\)이 \(N\)보다 클 때는
\[
\begin{align}
\begin{bmatrix}
Av_1 & Av_2 & \cdots & Av_N
\end{bmatrix}
=
\begin{bmatrix}
\sigma_1u_1 & \sigma_2u_2 & \cdots & \sigma_Nu_N
\end{bmatrix}
\tag{3.4.22}
\end{align}
\]
이 되고 \(N\)이 \(M\)보다 클 때는
\[
\begin{align}
\begin{bmatrix}
Av_1 & Av_2 & \cdots & Av_M
\end{bmatrix}
=
\begin{bmatrix}
\sigma_1u_1 & \sigma_2u_2 & \cdots & \sigma_Mu_M
\end{bmatrix}
\tag{3.4.23}
\end{align}
\]
이 된다.
즉, \(i\)번째 특잇값 \(\sigma_i\)와 특이벡터 \(u_i\), \(v_i\)는 다음과 같은 관계가 있다.
\[
\begin{align}
Av_i = \sigma_i u_i \;\; (i=1, \ldots, \text{min}(M,N))
\tag{3.4.24}
\end{align}
\]
이 관계는 고유분해와 비슷하지만 고유분해와는 달리 좌변과 우변의 벡터가 다르다.
예제¶
위에서 예로 들었던 행렬의 경우,
\[\begin{split}
\begin{align}
\begin{bmatrix}
3 & -1 \\
1 & 3 \\
1 & 1
\end{bmatrix}
\begin{bmatrix}
-\frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}}
\end{bmatrix}
=
\sqrt{12}
\begin{bmatrix}
-\frac{1}{\sqrt{6}} \\ -\frac{2}{\sqrt{6}} \\ -\frac{1}{\sqrt{6}}
\end{bmatrix}
\tag{3.4.25}
\end{align}
\end{split}\]
\[\begin{split}
\begin{align}
\begin{bmatrix}
3 & -1 \\
1 & 3 \\
1 & 1
\end{bmatrix}
\begin{bmatrix}
\frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}}
\end{bmatrix}
=
\sqrt{10}
\begin{bmatrix}
\frac{2}{\sqrt{5}} \\
-\frac{1}{\sqrt{5}} \\
0 \\
\end{bmatrix}
\tag{3.4.26}
\end{align}
\end{split}\]
가 성립한다.
연습 문제 3.4.2¶
NumPy를 사용하여 다음 행렬에 대해
\[
\begin{align}
Av_i = \sigma_i u_i
\tag{3.4.27}
\end{align}
\]
가 성립한다는 것을 계산으로 보여라.
\[\begin{split}
\begin{align}
B =
\begin{bmatrix}
3 & 2 & 2 \\
2 & 3 & -2
\end{bmatrix}
\tag{3.4.28}
\end{align}
\end{split}\]
\[\begin{split}
\begin{align}
C =
\begin{bmatrix}
2 & 4 \\
1 & 3 \\
0 & 0 \\
0 & 0 \\
\end{bmatrix}
\tag{3.4.29}
\end{align}
\end{split}\]
특이분해와 고유분해의 관계¶
행렬 \(A\)의 분산행렬 \(A^TA^{}\)는
\[
\begin{align}
A^TA^{}
= (V^{} \Sigma^T U^T)( U^{}\Sigma^{} V^T)
= V^{} \Lambda^{} V^T
\tag{3.4.30}
\end{align}
\]
가 되어 행렬 \(A\)의 특잇값의 제곱(과 0)이 분산행렬 \(A^TA^{}\)의 고유값, 행렬 \(A\)의 오른쪽 특이벡터가 분산행렬 \(A^TA^{}\)의 고유벡터가 된다.
위 식에서 \(\Lambda\)은 \(N\)이 \(M\)보다 크면
\[\begin{split}
\begin{align}
\Lambda
=
\begin{bmatrix}
\sigma_1^2 & 0 & \cdots & 0 \\
0 & \sigma_2^2 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \sigma_M^2 \\
\end{bmatrix}
\tag{3.4.31}
\end{align}
\end{split}\]
이고 \(N\)이 \(M\)보다 작으면
\[\begin{split}
\begin{align}
\Lambda
=
\begin{bmatrix}
\sigma_1^2 & 0 & \cdots & 0 & \cdots & 0 \\
0 & \sigma_2^2 & \cdots & 0 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
0 & 0 & \cdots & \sigma_N^2 & \cdots & 0 \\
\vdots & \vdots & \cdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 0 & \cdots & 0 \\
\end{bmatrix}
= \text{diag}(\sigma_1^2, \sigma_2^2, \cdots, \sigma_N^2, 0, \cdots, 0)
\tag{3.4.32}
\end{align}
\end{split}\]
이다.
마찬가지 방법으로 행렬 \(A\)의 왼쪽 특이벡터가 행렬 \(AA^T\)의 고유벡터가 된다는 것을 증명할 수 있다.
w, V = np.linalg.eig(A.T @ A)
w # A.T A의 고윳값
array([12., 10.])
S ** 2 # A의 특잇값의 제곱
array([12., 10.])
V # A.T A의 고유벡터
array([[ 0.70710678, -0.70710678],
[ 0.70710678, 0.70710678]])
VT.T # A의 오른쪽 특이벡터
array([[-0.70710678, 0.70710678],
[-0.70710678, -0.70710678]])
연습 문제 3.4.3¶
NumPy를 사용하여 행렬 \(A\)의 왼쪽 특이벡터가 행렬 \(AA^T\)의 고유벡터가 된다는 것을 보여라.
\[\begin{split}
\begin{align}
A =
\begin{bmatrix}
3 & -1 \\
1 & 3 \\
1 & 1
\end{bmatrix}
\tag{3.4.33}
\end{align}
\end{split}\]
1차원 근사¶
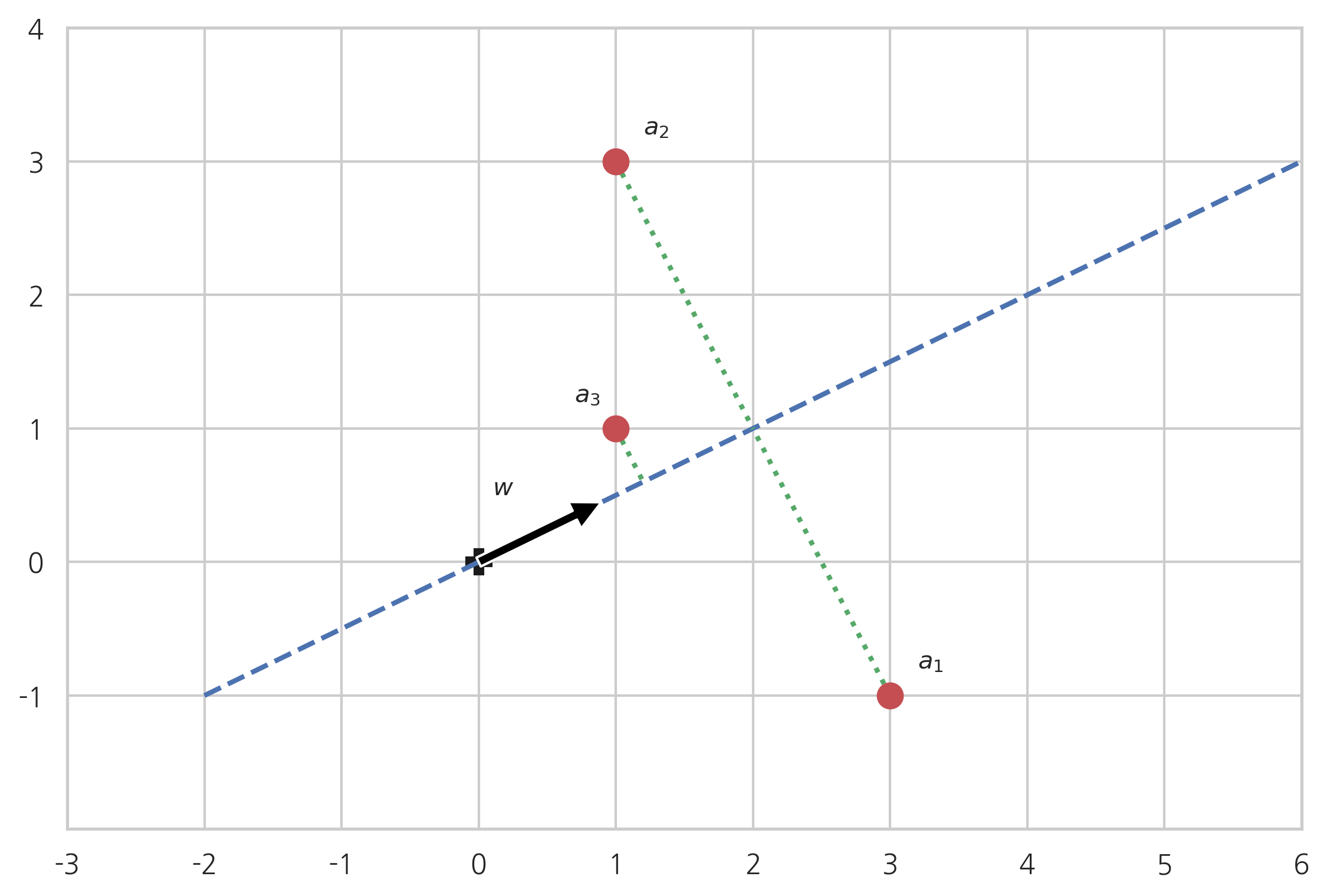
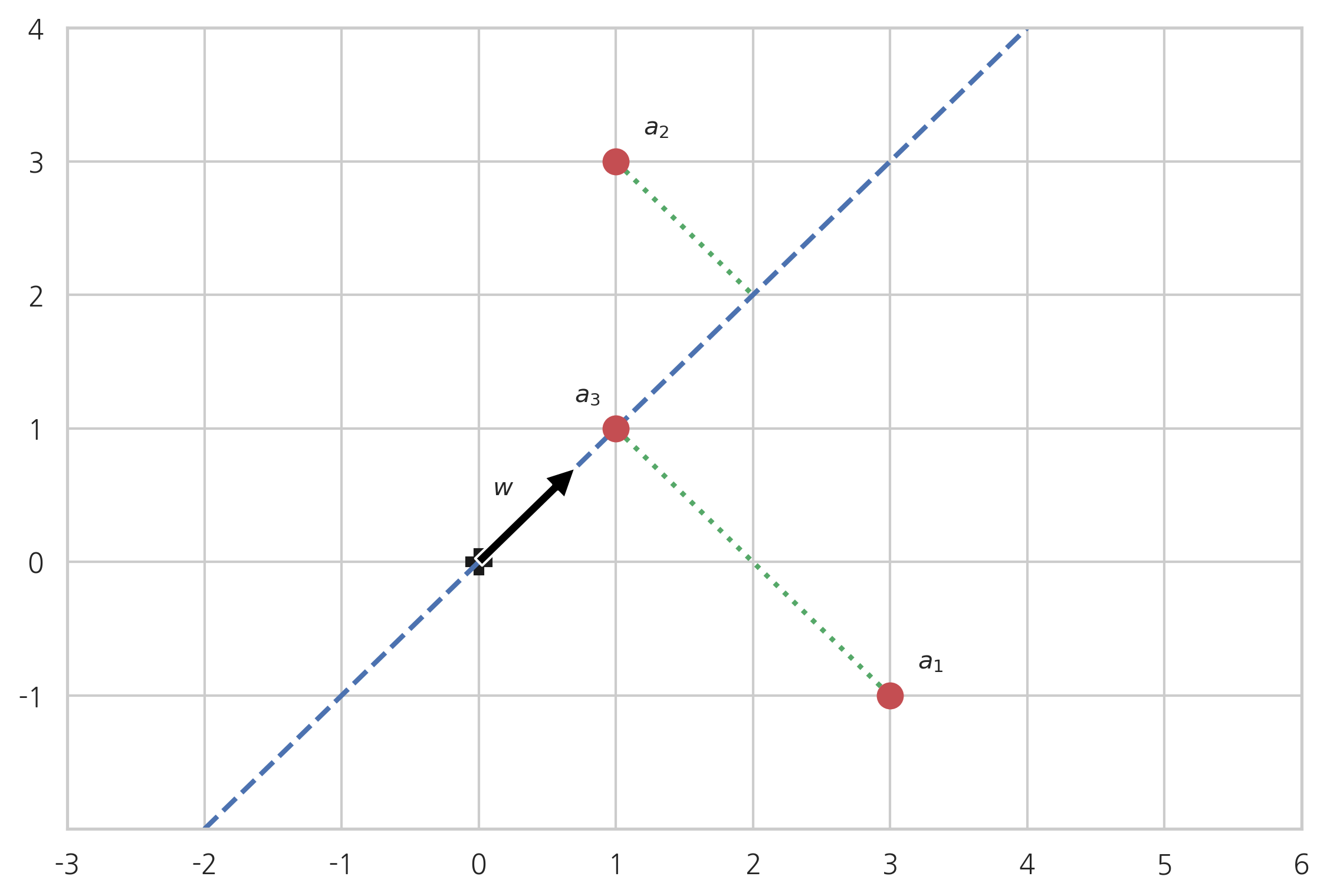
2차원 평면 위에 3개의 2차원 벡터 \(a_1, a_2, a_3\)가 있다. 원점을 지나면서 모든 점들과 가능한 한 가까이 있는 직선을 만들고 싶다면 직선의 방향을 어떻게 해야 할까? 직선의 방향을 나타내는 단위 벡터를 \(w\)라고 하자.
w = np.array([2, 1]) / np.sqrt(5)
a1 = np.array([3, -1])
a2 = np.array([1, 3])
a3 = np.array([1, 1])
black = {"facecolor": "black"}
plt.figure(figsize=(9, 6))
plt.plot(0, 0, 'kP', ms=10)
plt.annotate('', xy=w, xytext=(0, 0), arrowprops=black)
plt.plot([-2, 8], [-1, 4], 'b--', lw=2)
plt.plot([a1[0], 2], [a1[1], 1], 'g:', lw=2)
plt.plot([a2[0], 2], [a2[1], 1], 'g:', lw=2)
plt.plot([a3[0], 1.2], [a3[1], 0.6], 'g:', lw=2)
plt.plot(a1[0], a1[1], 'ro', ms=10)
plt.plot(a2[0], a2[1], 'ro', ms=10)
plt.plot(a3[0], a3[1], 'ro', ms=10)
plt.text(0.1, 0.5, "$w$")
plt.text(a1[0] + 0.2, a1[1] + 0.2, "$a_1$")
plt.text(a2[0] + 0.2, a2[1] + 0.2, "$a_2$")
plt.text(a3[0] - 0.3, a3[1] + 0.2, "$a_3$")
plt.xticks(np.arange(-3, 15))
plt.yticks(np.arange(-1, 5))
plt.xlim(-3, 6)
plt.ylim(-2, 4)
plt.show()
벡터 \(w\)와 점 \(a_i\)의 거리의 제곱은 다음처럼 계산할 수 있다.(연습 문제 3.1.9)
\[
\begin{align}
\Vert a_i^{\perp w}\Vert^2 = \Vert a_i\Vert^2 - \Vert a_i^{\Vert w}\Vert^2 = \Vert a_i\Vert^2 - (a_i^Tw)^2
\tag{3.4.34}
\end{align}
\]
벡터 \(a_1, a_2, a_3\)를 행벡터로 가지는 행렬 \(A\)를 가정하면
\[\begin{split}
\begin{align}
A = \begin{bmatrix} a_1^T \\ a_2^T \\ a_3^T \end{bmatrix}
\tag{3.4.35}
\end{align}
\end{split}\]
행벡터의 놈의 제곱의 합은 행렬의 놈이므로 모든 점들과의 거리의 제곱의 합은 행렬의 놈으로 계산된다. (연습 문제 2.3.2)
\[\begin{split}
\begin{align}
\begin{aligned}
\sum_{i=1}^3 \Vert a_i^{\perp w}\Vert^2
&= \sum_{i=1}^3 \Vert a_i\Vert^2 - \sum_{i=1}^3 (a_i^Tw)^2 \\
&= \Vert A \Vert^2 - \Vert Aw\Vert^2 \\
\end{aligned}
\tag{3.4.36}
\end{align}
\end{split}\]
점 \(a_i\)의 위치가 고정되어 있으므로 행렬 \(A\)의 놈 값은 고정되어 있다. 따라서 이 값이 가장 작아지려면 \(\Vert Aw\Vert^2\)의 값이 가장 크게 만드는 \(w\)를 찾아야 한다.이 문제는 다음처럼 수식으로 쓸 수 있다.
\[
\begin{align}
\arg\max_w \Vert Aw \Vert^2
\tag{3.4.37}
\end{align}
\]
1차원 근사의 풀이¶
위에서 예로 든 행렬 \(A \in \mathbf{R}^{3 \times 2}\)를 특이분해하면 2개의 특잇값, 왼쪽/오른쪽 특이벡터를 가진다. 이를 각각 다음처럼 이름붙인다.
첫 번째 특잇값: \(\sigma_1\), 첫 번째 왼쪽 특이벡터 \(u_1 \in \mathbf{R}^{3}\), 첫 번째 오른쪽 특이벡터 \(v_1 \in \mathbf{R}^{2}\)
두 번째 특잇값: \(\sigma_2\), 두 번째 왼쪽 특이벡터 \(u_2 \in \mathbf{R}^{3}\), 두 번째 오른쪽 특이벡터 \(v_2 \in \mathbf{R}^{2}\)
첫 번째 특잇값 \(\sigma_1\)은 두 번째 특잇값 \(\sigma_2\)보다 같거나 크다.
\[
\begin{align}
\sigma_1 \geq \sigma_2
\tag{3.4.38}
\end{align}
\]
또한 위에서 알아낸 것처럼 A에 오른쪽 특이벡터를 곱하면 왼쪽 특이벡터 방향이 된다.
\[
\begin{align}
A v_1 = \sigma_1 u_1
\tag{3.4.39}
\end{align}
\]
\[
\begin{align}
A v_2 = \sigma_2 u_2
\tag{3.4.40}
\end{align}
\]
오른쪽 특이벡터 \(v_1, v_2\)는 서로 직교하므로 (같은 방향이 아니라서) 선형독립이고 2차원 평면공간의 기저벡터가 될 수 있다.
우리는 \(\Vert Aw\Vert\)의 값이 가장 크게 만드는 \(w\)를 찾아야 하는데 \(w\)는 2차원 벡터이므로 2차원 평면공간의 기저벡터인 \(v_1, v_2\)의 선형조합으로 표현할 수 있다.
\[
\begin{align}
w = w_{1} v_1 + w_{2} v_2
\tag{3.4.41}
\end{align}
\]
단, \(w\)도 단위벡터이므로 \(w_{1}, w_{2}\)는 다음 조건을 만족해야 한다.
\[
\begin{align}
w_{1}^2 + w_{2}^2 = 1
\tag{3.4.42}
\end{align}
\]
이때 \(\Vert Aw\Vert\)의 값은
\[\begin{split}
\begin{align}
\begin{aligned}
\Vert Aw\Vert^2
&= \Vert A(w_{1} v_1 + w_{2} v_2)\Vert^2 \\
&= \Vert w_{1}Av_1 + w_{2}Av_2 \Vert^2 \\
&= \Vert w_{1} \sigma_1 u_1 + w_{2} \sigma_2 u_2 \Vert^2 \\
&= \Vert w_{1} \sigma_1 u_1 \Vert^2 + \Vert w_{2} \sigma_2 u_2 \Vert^2 \;\; \text{(orthogonal)} \\
&= w_{1}^2 \sigma_1^2 \Vert u_1 \Vert^2 + w_{2}^2 \sigma_2^2 \Vert u_2 \Vert^2 \\
&= w_{1}^2 \sigma_1^2 + w_{2}^2 \sigma_2^2 \;\; \text{(unit vector)}\\
\end{aligned}
\tag{3.4.43}
\end{align}
\end{split}\]
\(\sigma_1 > \sigma_2 > 0\) 이므로 \(w_{1}^2 + w_{2}^2 = 1\)라는 조건을 만족하면서 위 값을 가장 크게 하는 \(w_{1}, w_{2}\)값은
\[
\begin{align}
w_{1} = 1, w_{2} = 0
\tag{3.4.44}
\end{align}
\]
이다. 즉, 첫 번째 오른쪽 특이벡터 방향으로 하는 것이다.
\[
\begin{align}
w = v_1
\tag{3.4.45}
\end{align}
\]
이때 \(\Vert Aw\Vert\)는 첫 번째 특잇값이 된다.
\[
\begin{align}
\Vert Aw\Vert = \Vert Av_1\Vert = \Vert \sigma_1 u_1\Vert = \sigma_1 \Vert u_1\Vert = \sigma_1
\tag{3.4.46}
\end{align}
\]
위에서 예로 들었던 행렬
\[\begin{split}
\begin{align}
A =
\begin{bmatrix}
3 & -1 \\
1 & 3 \\
1 & 1
\end{bmatrix}
\tag{3.4.47}
\end{align}
\end{split}\]
첫 번째 오른쪽 특이벡터
\[\begin{split}
\begin{align}
v_1 =
\begin{bmatrix}
\frac{\sqrt{2}}{2} \\
\frac{\sqrt{2}}{2} \\
\end{bmatrix}
\tag{3.4.48}
\end{align}
\end{split}\]
가 가장 거리의 합이 작은 방향이 된다. 그리고 이때의 거리의 제곱의 합은 다음과 같다.
\[
\begin{align}
\Vert A \Vert^2 - \Vert Aw\Vert^2
=\Vert A \Vert^2 - \sigma_1^2
\tag{3.4.49}
\end{align}
\]
np.linalg.norm(A)**2 - S[0]**2
9.999999999999998
w = np.array([1, 1]) / np.sqrt(2)
a1 = np.array([3, -1])
a2 = np.array([1, 3])
a3 = np.array([1, 1])
black = {"facecolor": "black"}
plt.figure(figsize=(9, 6))
plt.plot(0, 0, 'kP', ms=10)
plt.annotate('', xy=w, xytext=(0, 0), arrowprops=black)
plt.plot([-2, 4], [-2, 4], 'b--', lw=2)
plt.plot([a1[0], 1], [a1[1], 1], 'g:', lw=2)
plt.plot([a2[0], 2], [a2[1], 2], 'g:', lw=2)
plt.plot(a1[0], a1[1], 'ro', ms=10)
plt.plot(a2[0], a2[1], 'ro', ms=10)
plt.plot(a3[0], a3[1], 'ro', ms=10)
plt.text(0.1, 0.5, "$w$")
plt.text(a1[0] + 0.2, a1[1] + 0.2, "$a_1$")
plt.text(a2[0] + 0.2, a2[1] + 0.2, "$a_2$")
plt.text(a3[0] - 0.3, a3[1] + 0.2, "$a_3$")
plt.xticks(np.arange(-3, 15))
plt.yticks(np.arange(-1, 5))
plt.xlim(-3, 6)
plt.ylim(-2, 4)
plt.show()
일반적인 풀이¶
만약 \(N=3\)이 아니라 일반적인 경우에는 다음처럼 풀 수 있다.
\[\begin{split}
\begin{align}
\begin{aligned}
\Vert Aw \Vert^2
&= \sum_{i=1}^{N} (a_i^Tw)^2 \\
&= \sum_{i=1}^{N} (a_i^Tw)^T(a_i^Tw) \\
&= \sum_{i=1}^{N} w^Ta_ia_i^Tw \\
&= w^T \left( \sum_{i=1}^{N} a_ia_i^T \right) w \\
&= w^T A^TA w \\
\end{aligned}
\tag{3.4.50}
\end{align}
\end{split}\]
분산행렬의 고유분해 공식을 이용하면,
\[\begin{split}
\begin{align}
\begin{aligned}
w^T A^TA w
&= w^T V \Lambda V^T w \\
&= w^T \left( \sum_{i=1}^{M} \sigma^2_iv_iv_i^T \right) w \\
&= \sum_{i=1}^{M}\sigma^2_i(w^Tv_i)(v_i^Tw) \\
&= \sum_{i=1}^{M}\sigma^2_i\Vert v_i^Tw\Vert^2 \\
\end{aligned}
\tag{3.4.51}
\end{align}
\end{split}\]
이 된다. 이 식에서 \(M\)은 0이 아닌 특잇값 개수다.
즉, 우리가 풀어야 할 문제는 다음과 같다.
\[
\begin{align}
\arg\max_w \Vert Aw \Vert^2 = \arg\max_w \sum_{i=1}^{M}\sigma^2_i\Vert v_i^Tw\Vert^2
\tag{3.4.52}
\end{align}
\]
이 값을 가장 크게 하려면 \(w\)를 가장 큰 특잇값에 대응하는 오른쪽 고유벡터 \(v_1\)으로 해야 한다.
랭크-1 근사문제¶
또 \(a_i\)를 \(w\)에 투영한 벡터는
\[
\begin{align}
a^{\Vert w}_i = (a_i^Tw)w
\tag{3.4.53}
\end{align}
\]
이므로 \(w\) 벡터를 이용하면 \(N\)개의 \(M\)차원 벡터 \(a_1, a_2, \cdots, a_N\;(a_i \in \mathbf{R}^M)\)를 1차원으로 투영(projection)하여 가장 비슷한 \(N\)개의 1차원 벡터 \(a^{\Vert w}_1, a^{\Vert w}_2, \cdots, a^{\Vert w}_N\;(a^{\Vert w}_i \in \mathbf{R}^1)\)를 만들 수 있다.
\[\begin{split}
\begin{align}
A'=
\begin{bmatrix}
\left(a^{\Vert w}_1\right)^T \\
\left(a^{\Vert w}_2\right)^T \\
\vdots \\
\left(a^{\Vert w}_N\right)^T
\end{bmatrix}
=
\begin{bmatrix}
a_1^Tw^{}w^T \\
a_2^Tw^{}w^T \\
\vdots \\
a_N^Tw^{}w^T
\end{bmatrix}
=
\begin{bmatrix}
a_1^T \\
a_2^T \\
\vdots \\
a_N^T
\end{bmatrix}
w^{}w^T
=
Aw^{}w^T
\tag{3.4.54}
\end{align}
\end{split}\]
이 답은 원래 행렬 \(A\)에 랭크-1 행렬 \(w^{}w^T\)를 곱해서 원래의 행렬 \(A\)와 가장 비슷한 행렬 \(A'\)을 만드는 문제와 같다.
\[
\begin{align}
\arg\min_w \Vert A - A' \Vert = \arg\min_w \Vert A^{} - A^{}w^{}w^T \Vert
\tag{3.4.55}
\end{align}
\]
따라서 문제를 **랭크-1 근사문제(rank-1 approximation problem)**라고도 한다.
\(K\)차원 근사¶
이번에는 \(N\)개의 \(M\)차원 벡터 \(a_1, a_2, \cdots, a_N\;(a_i \in \mathbf{R}^M)\)를 1차원이 아니라 정규직교인 기저벡터 \(w_1, w_2, \cdots, w_K\)로 이루어진 \(K\)차원 벡터공간으로 투영하여 가장 비슷한 \(N\)개의 \(K\)차원 벡터 \(a^{\Vert w}_1, a^{\Vert w}_2, \cdots, a^{\Vert w}_N\;\)를 만들기 위한 정규직교 기저벡터 \(w_1, w_2, \cdots, w_K\)를 찾는 문제를 생각하자. 이 문제는 랭크-\(K\) 근사문제라고 한다.
기저벡터행렬을 \(W\)라고 하자.
\[
\begin{align}
W = \begin{bmatrix} w_1 & w_2 & \cdots & w_K \end{bmatrix}
\tag{3.4.56}
\end{align}
\]
정규직교 기저벡터에 대한 벡터 \(a_i\)의 투영 \(a^{\Vert w}_i\)는 각 기저벡터에 대한 내적으로 만들 수 있다.
\[\begin{split}
\begin{align}
\begin{aligned}
a^{\Vert w}_i
&=
(a_i^Tw_1)w_1 +
(a_i^Tw_2)w_2 +
\cdots
+ (a_i^Tw_K)w_K \\
\end{aligned}
=
\sum_{k=1}^K (a_i^Tw_k)w_k
\tag{3.4.57}
\end{align}
\end{split}\]
벡터 \(a_1, a_2, \cdots, a_N\)를 행벡터로 가지는 행렬 \(A\)를 가정하면
\[\begin{split}
\begin{align}
A = \begin{bmatrix} a_1^T \\ a_2^T \\ \vdots \\ a_N^T \end{bmatrix}
\tag{3.4.58}
\end{align}
\end{split}\]
모든 점들과의 거리의 제곱의 합은 다음처럼 행렬의 놈으로 계산할 수 있다.
\[\begin{split}
\begin{align}
\begin{aligned}
\sum_{i=1}^N \Vert a_i^{\perp w}\Vert^2
&= \sum_{i=1}^N \Vert a_i\Vert^2 - \sum_{i=1}^N \Vert a^{\Vert w}_i\Vert^2 \\
&= \Vert A \Vert^2 - \sum_{i=1}^N \Vert a^{\Vert w}_i\Vert^2 \\
\end{aligned}
\tag{3.4.59}
\end{align}
\end{split}\]
행렬 \(A\)는 이미 주어져있으므로 이 값을 가장 작게 하려면 두 번째 항의 값을 가장 크게 하면 된다. 두 번째 항은 K=1일 때와 같은 방법으로 분산행렬 형태로 바꿀 수 있다.
\[\begin{split}
\begin{align}
\begin{aligned}
\sum_{i=1}^N \Vert a^{\Vert w}_i\Vert^2
&= \sum_{i=1}^N \sum_{k=1}^K \Vert (a_i^Tw_k)w_k \Vert^2 \\
&= \sum_{i=1}^N \sum_{k=1}^K \Vert a_i^Tw_k \Vert^2 \\
&= \sum_{k=1}^K w_k^T A^TA w_k \\
\end{aligned}
\tag{3.4.60}
\end{align}
\end{split}\]
분산행렬의 고유분해를 사용하면
\[\begin{split}
\begin{align}
\begin{aligned}
\sum_{k=1}^K w_k^T A^TA w_k
&= \sum_{k=1}^K w_k^T V \Lambda V^T w_k \\
&= \sum_{k=1}^K w_k^T \left( \sum_{i=1}^{M} \sigma^2_iv_iv_i^T \right) w_k \\
&= \sum_{k=1}^K \sum_{i=1}^{M}\sigma^2_i\Vert v_i^Tw_k\Vert^2 \\
\end{aligned}
\tag{3.4.61}
\end{align}
\end{split}\]
이 문제도 1차원 근사문제처럼 풀면 다음과 같은 답을 얻을 수 있다.
가장 큰 \(K\)개의 특잇값에 대응하는 오른쪽 특이벡터가 기저벡터일 때 가장 값이 커진다.
랭크-K 근사문제¶
우리가 찾아야 하는 것은 이 값을 가장 크게 하는 \(K\)개의 영벡터가 아닌 직교하는 단위벡터 \(w_k\)이다. 고유분해의 성질로부터 오른쪽 기저벡터 중 가장 큰 \(K\)개의 특잇값에 대응하는 오른쪽 특이벡터가 우리가 찾는 기저벡터가 된다.
이 문제는 다음처럼 랭크-\(K\) 근사문제의 형태로 만들 수도 있다.
\[\begin{split}
\begin{align}
\begin{aligned}
a^{\Vert w}_i
&=
(a_i^Tw_1)w_1 +
(a_i^Tw_2)w_2 +
\cdots
+ (a_i^Tw_K)w_K \\
&=
\begin{bmatrix} w_1 & w_2 & \cdots & w_K \end{bmatrix}
\begin{bmatrix} a_i^Tw_1 \\ a_i^Tw_2 \\ \vdots \\ a_i^Tw_K \end{bmatrix} \\
&=
\begin{bmatrix} w_1 & w_2 & \cdots & w_K \end{bmatrix}
\begin{bmatrix} w_1^T \\ w_2^T \\ \vdots \\ w_K^T \end{bmatrix} a_i \\
&=
WW^Ta_i
\end{aligned}
\tag{3.4.62}
\end{align}
\end{split}\]
이러한 투영벡터를 모아놓은 행렬 \(A'\)는
\[\begin{split}
\begin{align}
A'=
\begin{bmatrix}
\left(a^{\Vert w}_1\right)^T \\
\left(a^{\Vert w}_2\right)^T \\
\vdots \\
\left(a^{\Vert w}_N\right)^T
\end{bmatrix}
=
\begin{bmatrix}
a_1^TW^{}W^T \\
a_2^TW^{}W^T\\
\vdots \\
a_N^TW^{}W^T
\end{bmatrix}
=
\begin{bmatrix}
a_1^T \\
a_2^T \\
\vdots \\
a_N^T
\end{bmatrix}
W^{}W^T
=
AW^{}W^T
\tag{3.4.63}
\end{align}
\end{split}\]
따라서 이 문제는 원래 행렬 \(A\)에 랭크-K 행렬 \(W_{}W^T\)를 곱해서 원래의 행렬 \(A\)와 가장 비슷한 행렬 \(A'\)을 만드는 문제와 같다.
\[
\begin{align}
\arg\min_{w_1,\cdots,w_K} \Vert A - AW^{}W^T \Vert
\tag{3.4.64}
\end{align}
\]