7.2 기댓값과 확률변수의 변환#
표본평균, 표본분산 등은 현실세계의 데이터 분포의 모양을 서술하는 특성값이다. 이제부터는 이론적인 확률분포함수의 모양을 서술하는 특성값을 살펴본다. 우선 기댓값부터 공부한다. 기댓값은 표본평균처럼 분포의 위치를 알려주는 특성값이지만 확률분포의 가중합이나 가중적분으로 정의한다.
확률변수의 기댓값#
확률변수의 확률밀도함수를 알면 확률변수의 이론적 평균값을 구할 수 있다. 이러한 이론적 평균을 확률변수의 **기댓값(expectation)**이라고 한다. 단순히 평균(mean)이라고 말하기도 한다.
확률변수 \(X\)의 기댓값을 구하는 연산자(operator)는 영어 Expectation의 첫 글자를 사용하여 \(\text{E}[X]\)로 표기한다. 기댓값은 그리스 문자 \(\mu_X\)로 표기한다. 확률변수를 혼동할 염려가 없으면 확률변수 이름은 생략하고 그냥 \(\mu\)라고 써도 된다.
이산확률변수의 기댓값은 표본공간의 원소 \(x_i\)의 가중평균이다. 이때 가중치는 \(x_i\)가 나올 수 있는 확률 즉 확률질량함수 \(p(x_i)\)이다.
예제#
공정한 주사위에서 나올 수 있는 숫자를 대표하는 확률변수 \(X\)는 나올 수 있는 값이 1, 2, 3, 4, 5, 6 이므로,
기댓값은 \(\dfrac{7}{2}\)이다.
예제#
공정하지 않은 주사위, 예들 들어 짝수가 나올 확률이 홀수가 나올 확률의 2배인 주사위에서 기댓값을 구하면 다음과 같다.
기댓값은 \(\dfrac{11}{3}\)이다.
연습 문제 7.2.1#
공정한 동전이 있고 이 동전의 앞면이 나오면 1, 뒷면이 나오면 0인 확률변수 \(X\)가 있다. 이 확률변수의 기댓값 \(\text{E}[X]\)을 구하라.
참고로 데이터 공간에서 기댓값에 대응하는 값인 표본평균을 구하는 공식은 다음과 같았다.
기댓값 공식과 표본평균 공식에서 \(x_i\)의 의미가 다르다는 점에 유의하라. 기댓값 공식에서 \(x_i\)는 표본공간의 모든 원소를 뜻하지만 표본평균 공식에서 \(x_i\)는 선택된(sampled, realized) 표본만을 뜻한다.
연습 문제 7.2.2#
기댓값을 구하는 공식에서는 확률을 가중치로 곱한다. 그런데 왜 표본평균을 구하는 공식에서는 확률 가중치가 없는가?
연속확률변수의 기댓값은 확률밀도함수 \(p(x)\)를 가중치로 하여 모든 가능한 표본 \(x\)를 적분한 값이다.

그림 7.2.1 : 기댓값 계산
기댓값은 여러 가능한 \(x\)값을 확률(또는 확률밀도)값에 따라 가중합을 한 것이므로 가장 확률(또는 확률밀도)이 높은 \(x\)값 근처의 값이 된다. 즉, 확률(또는 확률밀도)가 모여 있는 곳의 위치를 나타낸다.
예제#
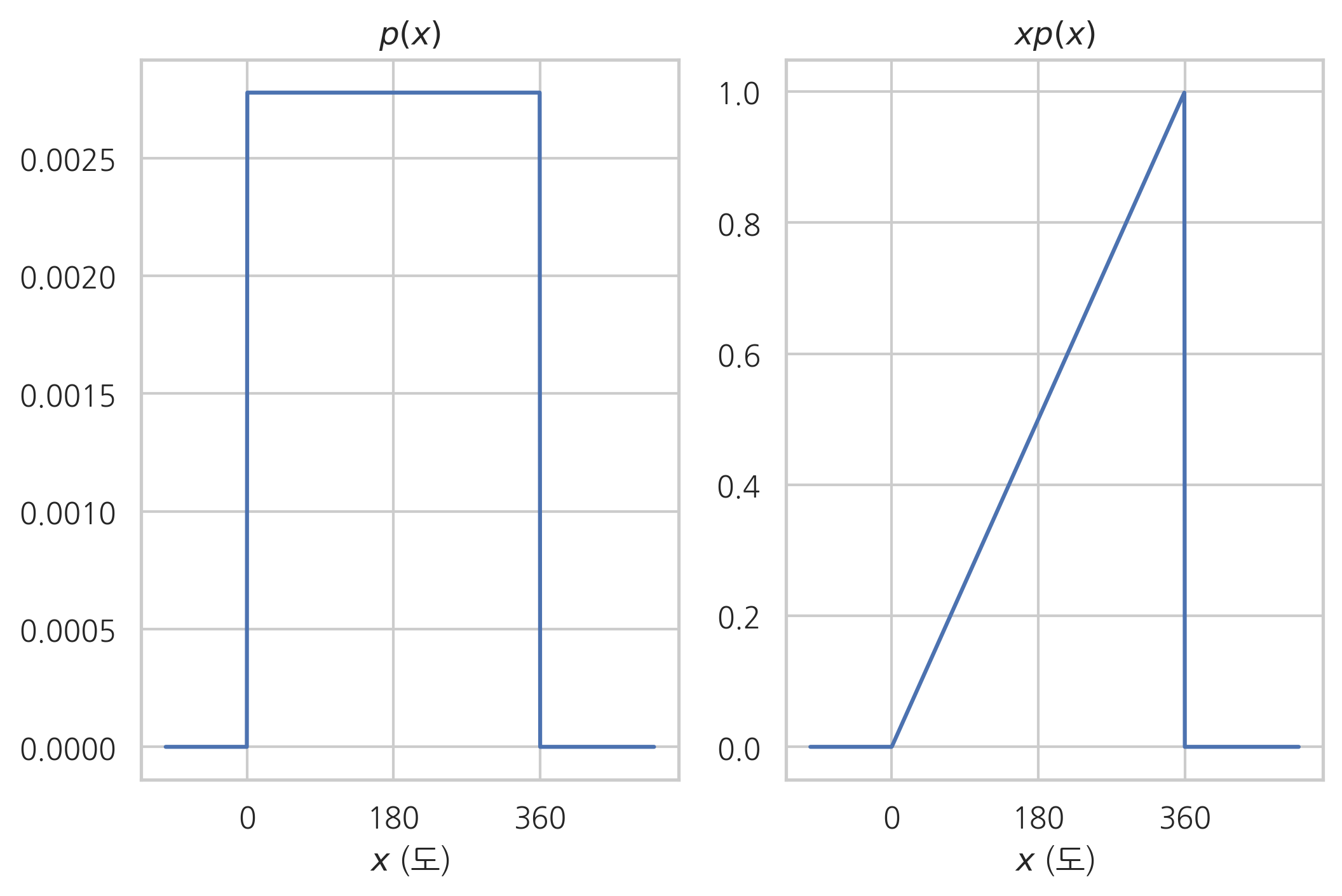
회전하는 원반을 이용하여 복권 번호를 결정하는 문제에서 확률밀도함수 \(p(x)\)와 여기에서 \(x\)가 곱해진 함수 \(xp(x)\)의 모양은 다음과 같다. 기댓값은 이 함수 \(xp(x)\)를 적분하여 구한 삼각형처럼 생긴 함수의 면적이다.
x = np.linspace(-100, 500, 1000)
p = np.zeros_like(x)
p[(0 < x) & (x <= 360)] = 1 / 360
xp = x * p
plt.subplot(121)
plt.plot(x, p)
plt.xticks([0, 180, 360])
plt.title("$p(x)$")
plt.xlabel("$x$ (도)")
plt.subplot(122)
plt.plot(x, xp)
plt.xticks([0, 180, 360])
plt.title("$xp(x)$")
plt.xlabel("$x$ (도)")
plt.show()
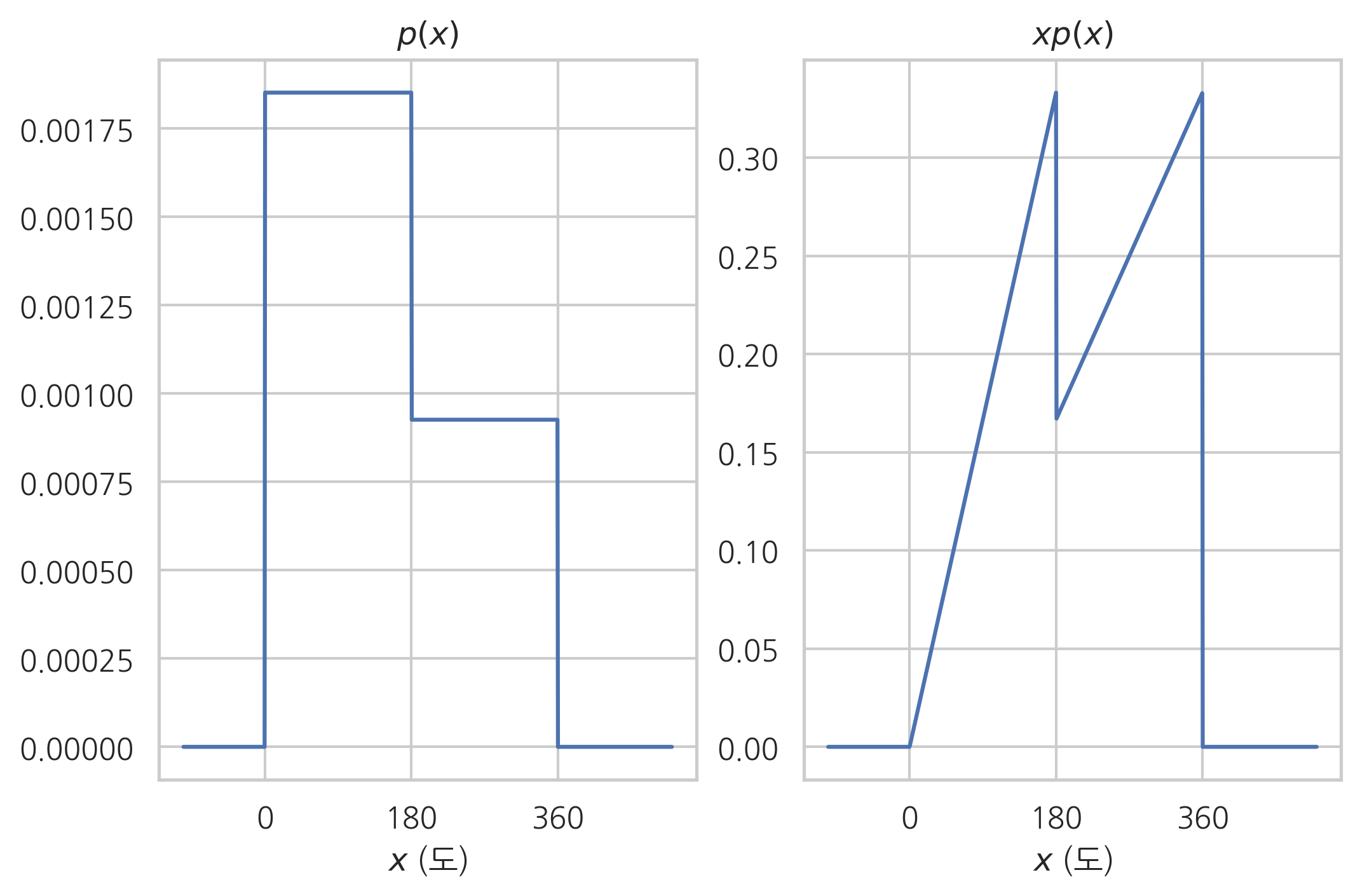
만약 0도에서 180도 사이에 화살이 2배 더 잘 박히도록 원반이 조작되었다면 확률밀도함수 \(p(x)\)와 여기에서 \(x\)가 곱해진 함수 \(xp(x)\) 모양은 다음과 같다. 기댓값은 이 함수 \(xp(x)\)를 적분하여 구한 함수의 면적이다.
x = np.linspace(-100, 500, 1000)
p = np.zeros_like(x)
p[(0 < x) & (x <= 180)] = 2 / (3 * 360)
p[(180 < x) & (x <= 360)] = 1 / (3 * 360)
xp = x * p
plt.subplot(121)
plt.plot(x, p)
plt.xticks([0, 180, 360])
plt.title("$p(x)$")
plt.xlabel("$x$ (도)")
plt.subplot(122)
plt.plot(x, xp)
plt.xticks([0, 180, 360])
plt.title("$xp(x)$")
plt.xlabel("$x$ (도)")\
plt.show()
연습 문제 7.2.3#
확률변수 \(Y\)는 0도에서 180도 사이에 화살이 2배 더 잘 박히도록 조작된 원반을 이용하여 복권 번호를 결정하는 문제에서 나오는 각도다. 확률변수 \(Y\)의 기댓값 \(\text{E}[Y]\)를 구하라.
확률변수의 변환#
우리가 얻은 데이터의 값을 어떤 함수 \(f\)에 넣어서 변화시킨다고 가정하자. 그러면 새로운 데이터 집합이 생긴다.
이 새로운 데이터를 \(\{y_i\}\)라고 부르자. \(\{y_i\}\)는 기존의 데이터와 다른 새로운 데이터이므로 다른 확률변수라고 볼 수 있다. 예를 들어 데이터 \(\{x_i\}\)를 만드는 확률변수가 \(X\)라면 데이터 \(\{y_i\}\)를 만드는 데이터는 \(Y\)라는 새로운 확률변수가 된다.
이렇게 **기존의 확률변수를 사용하여 새로운 확률변수를 만드는 것을 확률변수의 변환(transform)**이라고 한다. 함수 \(f\)를 사용해 확률변수를 변환할 때는 다음처럼 표기한다.
확률 변수의 변환은 여러 확률변수가 있을 때도 성립한다. 예를 들어 두 확률변수 \(X\)와 \(Y\)가 있다고 가정하였을 때, 새로운 확률변수 \(Z = X + Y\)는 확률변수 \(X\)에서 나온 값과 확률변수 \(Y\)에서 나온 값을 더한 값이 나오도록 하는 확률변수를 뜻한다.

그림 7.2.2 : 확률변수의 변환
연습 문제 7.2.4#
확률변수 \(X\)는 주사위를 던져 나오는 수를 나타내는 확률변수다. 그리고 \(Y\)는 주사위를 던져나오는 수에 2배를 한 수를 나타내는 확률변수다. \(X\), \(Y\)의 확률질량함수의 그래프를 각각 그려라.
확률변수 \(X\)에서 표본을 \(N\)번 뽑아서 그 값을 더하는 경우에는 다음처럼 원래 확률변수의 복사본 \(X_1, X_2, \ldots, X_N\)을 만든 다음 이 복사본 확률변수의 표본값을 더한 형태로 변환식을 써야 한다.
이렇게 복사본을 만들어 첨자를 붙이는 이유는 \(X_1\)과 \(X_2\)가 같은 확률분포를 가지는 확률변수이지만 표본값이 다르기 때문이다. 만약 다음과 같이 쓰면,
이 식은 다음처럼 전혀 다른 확률변수를 가리킨다.
연습 문제 7.2.5#
확률변수 \(X_1\)과 \(X_2\)는 각각 주사위를 던져 나오는 수를 나타내는 확률변수다. 그리고 \(Y\)는 두 주사위를 동시에 던져 나오는 수의 합을 나타내는 확률변수다. 확률변수 \(X_1\), \(X_2\), \(Y\)의 확률질량함수의 그래프를 각각 그려라.
기댓값의 성질#
기댓값은 다음과 같은 성질을 가진다는 것을 수학적으로 증명할 수 있다. 변환된 확률변수의 기댓값을 계산할 때는 기댓값의 성질을 이용한다.
확률변수가 아닌 상수 \(c\)에 대해
선형성
통계량#
확률변수 \(X\)로부터 데이터 집합 \(\{ x_1, x_2, \ldots, x_N \}\)을 얻었다고 하자. 이 **데이터 집합의 모든 값을 정해진 어떤 공식에 넣어서 하나의 숫자를 구한 것을 통계량(statistics)**이라고 한다. 예를 들어 표본의 합, 표본평균, 표본중앙값, 표본분산 등은 모두 통계량이다. 통계량도 확률변수의 변환에 포함된다.

그림 7.2.3 : 통계량
표본평균 확률변수#
확률변수로부터 \(N\)개의 표본을 만들어 이 표본집합의 표본평균을 구하면 이렇게 구한 표본평균 값도 확률변수가 된다. 표본평균 확률변수는 원래의 확률변수 이름에 윗줄(bar)을 추가하여 \(\bar{X}\)와 같이 표기한다. 예를 들어 확률변수 \(X\)에서 나온 표본으로 만들어진 표본평균 확률변수는 \(\bar{X}\)로 표기한다.
위 식에서 \(X_i\)는 \(i\)번째로 실현된 표본값을 생성하는 확률변수를 의미한다. 이 확률변수 \(X_i\)는 원래의 확률변수 \(X\)의 복사본이다.

그림 7.2.4 : 표본평균 확률변수
연습 문제 7.2.6#
표본평균 \(\bar{x}\)의 값은 확률적인 데이터이고 이를 생성하는 확률변수 \(\bar{X}\)는 위와 같이 정의할 수 있었다. 그렇다면 (편향)표본분산 \(s^2\)의 값은 확률적인 데이터인가? 만약 그렇다면 이를 생성하는 확률변수 \(S^2\)은 어떻게 정의해야 하는가?
기댓값과 표본평균의 관계#
표본평균도 확률변수이므로 기댓값이 존재한다. 표본평균의 기댓값은 원래의 확률변수의 기댓값과 같다는 것을 다음처럼 증명할 수 있다.
(증명)
이 식이 뜻하는 바는 다음과 같다.
표본평균은 확률변수의 기댓값 근처의 값이 된다.
예를 들어 공정한 주사위의 기댓값은 3.5이다. 이 주사위를 던져 나온 값의 평균 즉 표본평균은 3.62346 또는 3.40987처럼 항상 3.5 근처의 값이 나오게 된다.
중앙값#
확률변수의 중앙값(median)은 중앙값보다 큰 값이 나올 확률과 작은 값이 나올 확률이 0.5로 같은 값을 뜻한다. 따라서 다음과 같이 누적확률분포 \(F(x)\)에서 중앙값을 계산할 수 있다.

그림 7.2.5 : 중앙값
최빈값#
**이산확률분포에서는 가장 확률 값이 큰 수를 최빈값(most frequent value)**이라고 한다. 하지만 연속확률분포인 경우에는 어느 값에 대해서나 특정한 값이 나올 확률은 0(zero)이므로 연속확률분포의 최빈값(mode)은 확률밀도함수 \(p(x)\)의 값이 가장 큰 확률변수의 값으로 정의한다. 즉 확률밀도함수의 최댓값의 위치다.