10.2 조건부엔트로피#
이 절에서는 두 확률변수의 결합엔트로피와 조건부엔트로피를 정의하는 방법을 공부하고 분류문제에 어떻게 활용할 수 있는지 살펴본다.
결합엔트로피#
**결합엔트로피(joint entropy)**는 결합확률분포를 사용하여 정의한 엔트로피를 말한다.
이산확률변수 \(X\), \(Y\)에 대해 결합엔트로피는 다음처럼 정의한다.
이 식에서 \(K_X\), \(K_Y\)는 각각 X와 Y가 가질 수 있는 값의 개수고 \(p\)는 확률질량함수다.
연속확률변수 \(X\), \(Y\)에 대해 결합엔트로피는 다음처럼 정의한다.
이 식에서 \(p\)는 확률밀도함수다.
결합엔트로피도 결합확률분포라는 점만 제외하면 일반적인 엔트로피와 같다. 모든 경우에 대해 골고루 확률이 분포되어 있으면 엔트로피값이 커지고 특정한 한 가지 경우에 대해 확률이 모여있으면 엔트로피가 0에 가까와진다.
조건부엔트로피#
**조건부엔트로피(conditional entropy)**는 어떤 확률변수 \(X\)가 다른 확률변수 \(Y\)의 값을 예측하는데 도움이 되는지를 측정하는 방법 중의 하나다. 만약 확률변수 \(X\)의 값이 어떤 특정한 하나의 값을 가질 때 확률변수 \(Y\)도 마찬가지로 특정한 값이 된다면 \(X\)로 \(Y\)를 예측할 수 있다. 반대로 확률변수 \(X\)의 값이 어떤 특정한 하나의 값을 가져도 확률변수 \(Y\)가 여러 값으로 골고루 분포되어 있다면 \(X\)는 \(Y\)의 값을 예측하는데 도움이 안된다.
조건부엔트로피의 정의는 다음과 같이 유도한다. 확률변수 \(X\), \(Y\)가 모두 이산확률변수라고 가정하고 \(X\)가 특정한 값 \(x_i\)를 가질 때의 \(Y\)의 엔트로피 \(H[Y \mid X=x_i]\)는 다음처럼 조건부확률분포의 엔트로피로 정의한다.
조건부엔트로피는 확률변수 \(X\)가 가질 수 있는 모든 경우에 대해 \(H[Y \mid X=x_i]\)를 가중평균한 값으로 정의한다.
연속확률변수의 경우에는 다음과 같다.
따라서 조건부엔트로피의 최종적인 수학적 정의는 다음과 같다.
이산확률변수의 경우에는 다음처럼 정의한다.
연속확률변수의 경우에는 다음처럼 정의한다.
예측에 도움이 되는 경우#
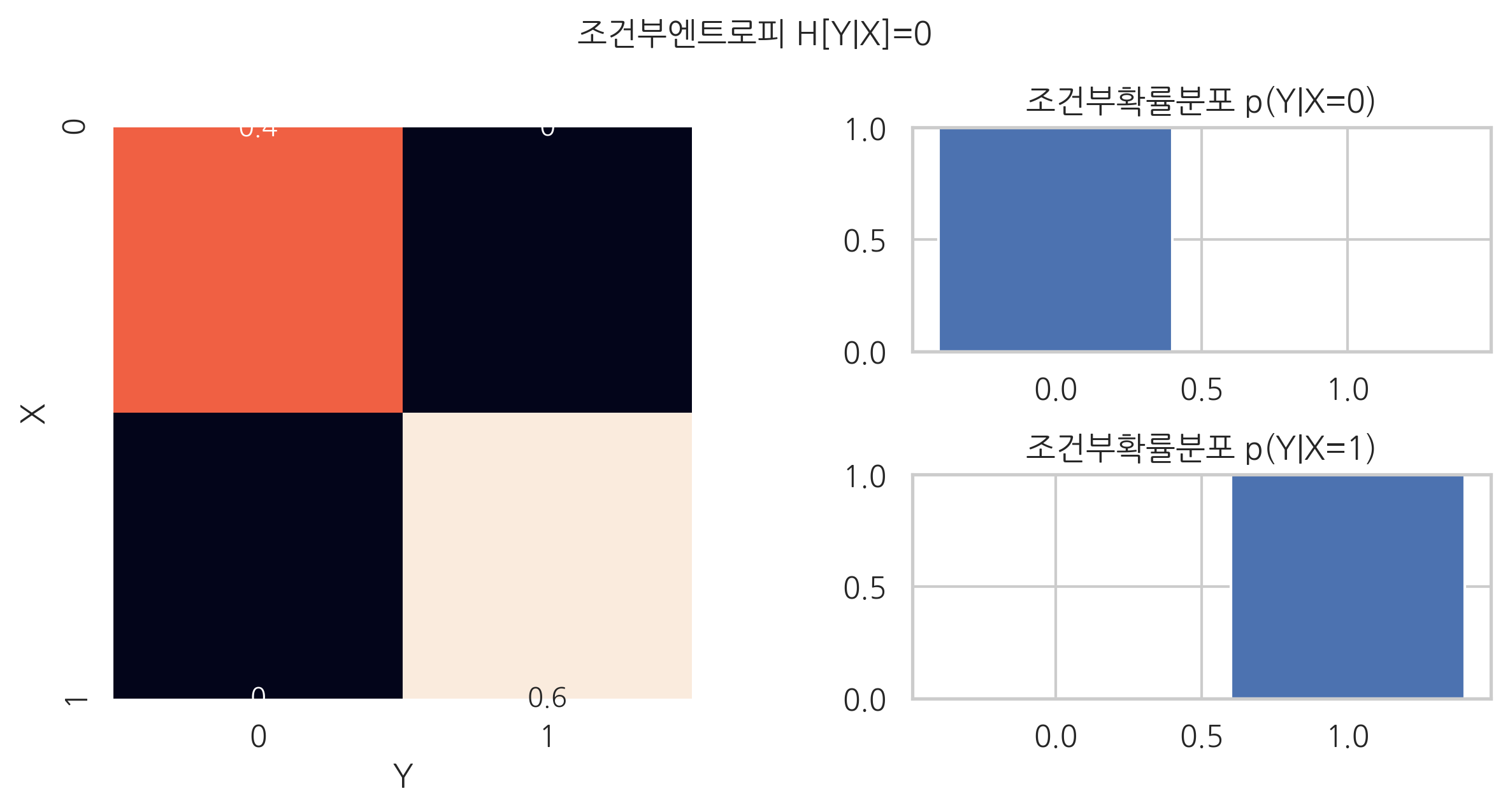
예를 들어 \(X\), \(Y\) 값의 관계가 다음과 같다고 하자.
\(Y = 0\) |
\(Y = 1\) |
|
|---|---|---|
\(X = 0\) |
0.4 |
0.0 |
\(X = 1\) |
0.0 |
0.6 |
\(X=0, X=1\)일 때의 조건부확률분포는 다음과 같다.
이때 \(Y\)의 엔트로피는 모두 0이다.
따라서 조건부엔트로피도 0이 된다.
plt.figure(figsize=(8, 4))
ax1 = plt.subplot(121)
pXY = [[0.4, 0], [0, 0.6]]
sns.heatmap(pXY, annot=True, cbar=False)
plt.xlabel("Y")
plt.ylabel("X")
plt.subplot(222)
plt.bar([0, 1], [1, 0])
plt.ylim(0, 1)
plt.title("조건부확률분포 p(Y|X=0)")
plt.subplot(224)
plt.bar([0, 1], [0, 1])
plt.ylim(0, 1)
plt.title("조건부확률분포 p(Y|X=1)")
plt.tight_layout(w_pad=5)
plt.suptitle("조건부엔트로피 H[Y|X]=0", y=1.05)
plt.show()
예측에 도움이 되지 않는 경우#
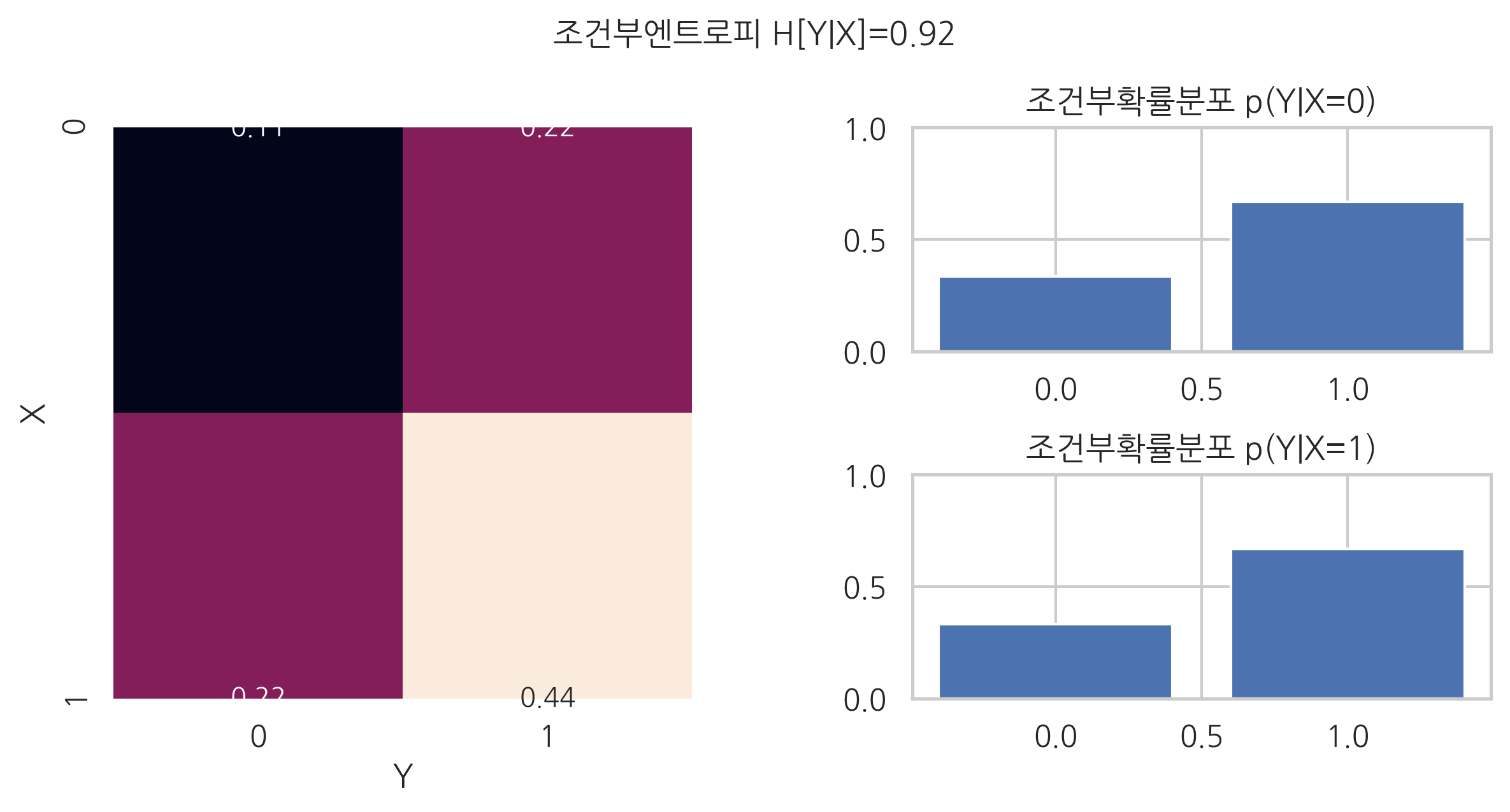
예를 들어 두 확률변수 \(X\), \(Y\) 값의 관계가 다음과 같다고 하자. 이 경우 두 확률변수는 서로 독립이다.
\(Y = 0\) |
\(Y = 1\) |
|
|---|---|---|
\(X = 0\) |
\(\frac{1}{9}\) |
\(\frac{2}{9}\) |
\(X = 1\) |
\(\frac{2}{9}\) |
\(\frac{4}{9}\) |
\(X=0, X=1\)일 때의 조건부확률분포는 다음과 같다.
두 경우 모두 \(Y\)의 엔트로피는 약 0.92다.
sp.stats.entropy([1/3, 2/3], base=2)
0.9182958340544894
이 값을 가중평균하면 조건부엔트로피값은 똑같이 약 0.92다.
plt.figure(figsize=(8, 4))
ax1 = plt.subplot(121)
pXY = [[1/9, 2/9], [2/9, 4/9]]
sns.heatmap(pXY, annot=True, cbar=False)
plt.xlabel("Y")
plt.ylabel("X")
plt.subplot(222)
plt.bar([0, 1], [1/3, 2/3])
plt.ylim(0, 1)
plt.title("조건부확률분포 p(Y|X=0)")
plt.subplot(224)
plt.bar([0, 1], [1/3, 2/3])
plt.ylim(0, 1)
plt.title("조건부확률분포 p(Y|X=1)")
plt.tight_layout(w_pad=5)
plt.suptitle("조건부엔트로피 H[Y|X]=0.92", y=1.05)
plt.show()
조건부엔트로피를 사용한 스팸메일 분류문제#
조건부엔트로피가 분류문제에 어떻게 도움이 되는지 알아보기 위해 스팸메일 분류문제를 살펴보자. 스팸메일 분류모형을 만들기 위한 학습용 메일 데이터가 80개 있다고 가정한다. 이 중 40개가 정상 메일(\(Y=0\)), 40개가 스팸 메일(\(Y=1\))이다.
스팸메일인지 아닌지를 특정 키워드가 존재하는지(\(X=1\)) 혹은 존재하지 않는지(\(X=0\))의 여부로 알아보고자 한다. 키워드 후보로는 \(X_1\), \(X_2\), \(X_3\) 세가지가 있다.
\(X_1\), \(Y\)의 관계는 다음과 같다.
\(Y = 0\) |
\(Y = 1\) |
||
|---|---|---|---|
\(X_1 = 0\) |
30 |
10 |
40 |
\(X_1 = 1\) |
10 |
30 |
40 |
40 |
40 |
80 |
\(X_2\), \(Y\)의 관계는 다음과 같다.
\(Y = 0\) |
\(Y = 1\) |
||
|---|---|---|---|
\(X_2 = 0\) |
20 |
40 |
60 |
\(X_2 = 1\) |
20 |
0 |
20 |
40 |
40 |
80 |
\(X_3\), \(Y\)의 관계는 다음과 같다.
\(Y = 0\) |
\(Y = 1\) |
||
|---|---|---|---|
\(X_3 = 0\) |
0 |
40 |
40 |
\(X_3 = 1\) |
40 |
0 |
40 |
40 |
40 |
80 |
이 세가지 키워드 중 하나만 골라야 한다면 어떤 키워드가 가장 좋은 키워드인가? 당연히 \(X_3\)다. 그렇다면 \(X_1\)과 \(X_2\) 중에서는 누가 더 좋은 키워드인가?
조건부엔트로피값을 사용하면 이 문제를 해결할 수 있다. 조건부엔트로피값이 가장 작아지는 것이 가장 좋은 키워드일 것이다.
\(X_1,Y\)의 조건부엔트로피는 다음과 같이 계산한다.
\(X_2,Y\)의 조건부엔트로피는 다음과 같이 계산한다.
\(X_3,Y\)의 조건부엔트로피는 다음과 같이 계산한다.
조건부엔트로피의 값으로부터 \(X_2\)가 \(X_1\)보다는 좋은 키워드임을 알 수 있다. 의사결정나무(decision tree)라는 분류모형은 조건부엔트로피를 사용하여 가장 좋은 특징값과 기준을 찾는다.
조건부엔트로피를 사용한 붓꽃 분류문제#
다음은 붓꽃 데이터 중 버지니카(virginica)와 베르시칼라(versicolor) 종의 데이터만 임포트하는 코드다.
from sklearn.datasets import load_iris
iris = load_iris()
idx = np.in1d(iris.target, [1, 2])
X = iris.data[idx, :]
y = iris.target[idx]
df = pd.DataFrame(X, columns=iris.feature_names)
df["species"] = iris.target[idx]
df.tail()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | species | |
|---|---|---|---|---|---|
| 95 | 6.7 | 3.0 | 5.2 | 2.3 | 2 |
| 96 | 6.3 | 2.5 | 5.0 | 1.9 | 2 |
| 97 | 6.5 | 3.0 | 5.2 | 2.0 | 2 |
| 98 | 6.2 | 3.4 | 5.4 | 2.3 | 2 |
| 99 | 5.9 | 3.0 | 5.1 | 1.8 | 2 |
sns.distplot(df[df.species == 1]["sepal length (cm)"], hist=True, rug=True, label="버지니카")
sns.distplot(df[df.species == 2]["sepal length (cm)"], hist=True, rug=True, label="베르시칼라")
plt.legend()
plt.xlabel("꽃받침의 길이")
plt.title("꽃받침의 길이와 붓꽃 종")
plt.show()
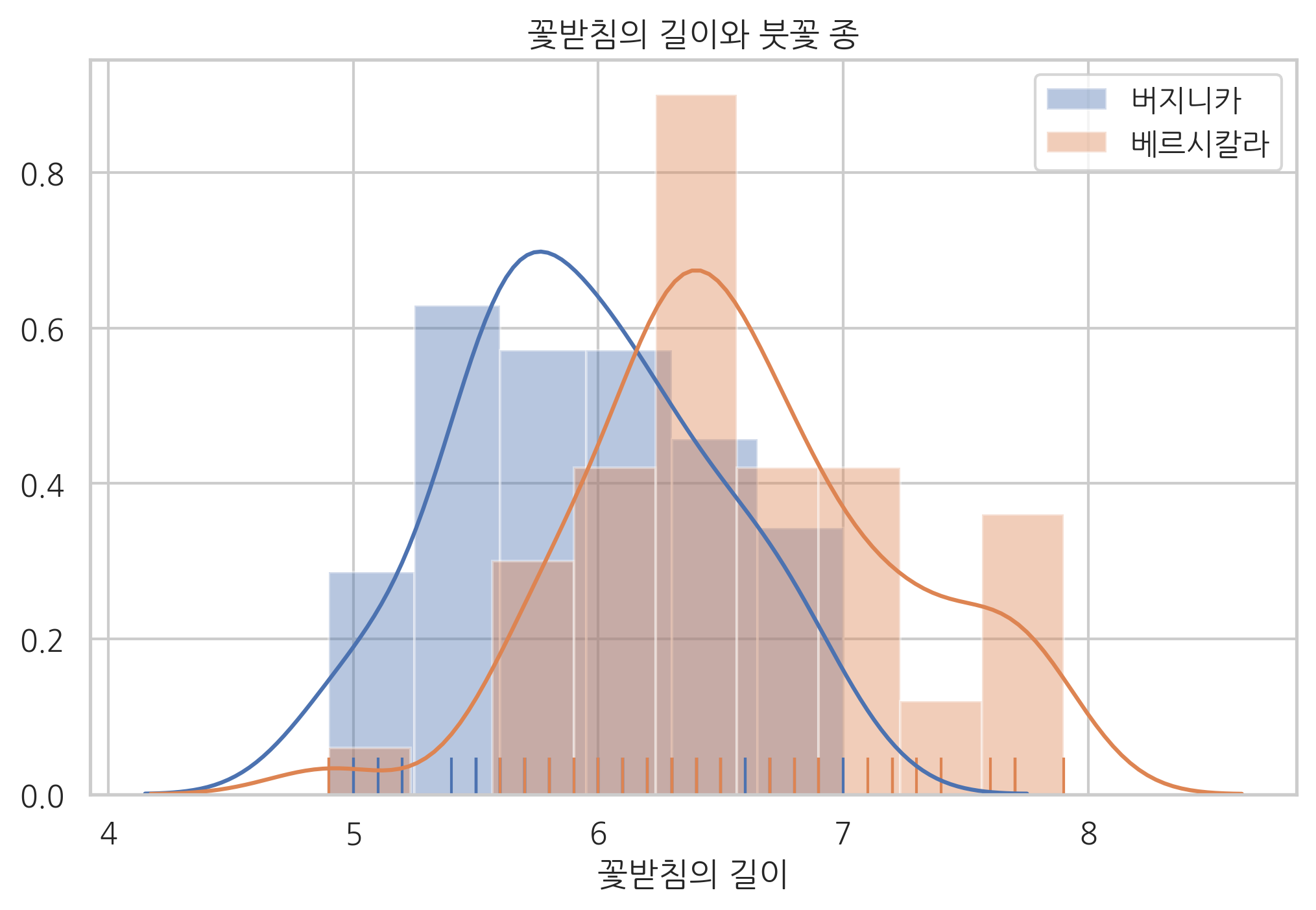
꽃받침의 길이(sepal length)로 두 종을 구별하고 싶다고 하자. 기준값을 무엇으로 정해야 할까?
만약 6cm를 기준으로 구분하면 다음과 같다.
df["X1"] = df["sepal length (cm)"] > 6
pivot_table1 = df.groupby(["X1", "species"]).size().unstack().fillna(0)
pivot_table1
| species | 1 | 2 |
|---|---|---|
| X1 | ||
| False | 30 | 9 |
| True | 20 | 41 |
이 때의 조건부엔트로피는 0.86이다.
def cond_entropy(v):
pYX0 = v[0, :] / np.sum(v[0, :])
pYX1 = v[1, :] / np.sum(v[1, :])
HYX0 = sp.stats.entropy(pYX0, base=2)
HYX1 = sp.stats.entropy(pYX1, base=2)
HYX = np.sum(v, axis=1) @ [HYX0, HYX1] / np.sum(v)
return HYX
cond_entropy(pivot_table1.values)
0.860714271586387
6.5cm를 기준으로 구분하면 다음과 같다.
df["X2"] = df["sepal length (cm)"] > 6.5
pivot_table2 = df.groupby(["X2", "species"]).size().unstack()
pivot_table2
| species | 1 | 2 |
|---|---|---|
| X2 | ||
| False | 42 | 28 |
| True | 8 | 22 |
이 때의 조건부엔트로피는 0.93이다.
cond_entropy(pivot_table2.values)
0.9306576387006182
따라서 6cm를 기준값으로 잡는 것이 6.5cm보다는 더 좋은 선택이다.
연습 문제 10.2.1#
(1) 붓꽃 데이터에서 꽃받침의 길이(sepal length)의 최솟값과 최댓값 구간을 0.05 간격으로 나누어 각각의 값을 기준값으로 하였을 때 조건부엔트로피가 어떻게 변하는지 그래프로 그려라.
(2) 꽃받침의 길이를 특징으로 사용하였을 때 어떤 값을 기준값으로 하는 것이 가장 좋은가?
(3) 꽃받침의 폭(sepal width)에 대해 위의 분석을 실시하라. 이 때는 기준값이 어떻게 되는가?
(4) 꽃받침의 길이(sepal length)와 꽃받침의 폭(sepal width) 중 하나를 특징으로 선택해야 한다면 어떤 것을 선택해야 하는가?