4.1 회귀분석 예제¶

특정한 입력변수값을 사용하여 출력변수의 값을 계산하는 것을 예측(prediction)문제라고 한다. 예측문제 중에서 출력변수의 값이 연속값인 문제를 회귀(regression) 또는 회귀분석(regression analysis) 문제라고 한다. 이 절에서는 회귀분석의 몇가지 예를 들어본다.

보스턴 집값 예측¶

sklearn 패키지의 datasets 서브패키지는 회귀분석을 공부하기 위한 예제를 제공한다. 그 중 load_boston() 명령으로 받을 수 있는 보스턴 주택 가격 데이터는 다음과 같은 데이터이다. 보스턴의 506개 타운(town)의 13개 독립변수값로부터 해당 타운의 주택가격 중앙값을 예측하는 문제다. 사용할 수 있는 특징 데이터는 다음과 같다.

독립변수
CRIM: 범죄율
INDUS: 비소매상업지역 면적 비율
NOX: 일산화질소 농도
RM: 주택당 방 수
LSTAT: 인구 중 하위 계층 비율
B: 인구 중 흑인 비율
PTRATIO: 학생/교사 비율
ZN: 25,000 평방피트를 초과 거주지역 비율
CHAS: 찰스강의 경계에 위치한 경우는 1, 아니면 0
AGE: 1940년 이전에 건축된 주택의 비율
RAD: 방사형 고속도로까지의 거리
DIS: 직업센터의 거리
TAX: 재산세율
종속변수
보스턴 506개 타운의 1978년 주택 가격 중앙값 (단위 1,000 달러)

load_boston 명령으로 받는 데이터 집합은 Bunch 라는 클래스 객체로 생성된다. 이 클래스 객체는 다음과 같은 속성을 가진다.

data: 독립변수 ndarray 배열
target: 종속변수 ndarray 배열
feature_names: 독립변수 이름 리스트
target_names: (옵션) 종속변수 이름 리스트
DESCR: (옵션) 자료에 대한 설명 문자열

from sklearn.datasets import load_boston

boston = load_boston()
dir(boston)

['DESCR', 'data', 'feature_names', 'filename', 'target']

분석할 데이터는 pandas 데이터프레임 형태로 만들어야 한다. 여기에서는 독립변수 행렬을 dfX로, 종속변수 벡터를 dfy로 만든다. 종속변수의 이름은 MEDV로 지정한다.

dfX = pd.DataFrame(boston.data, columns=boston.feature_names)
dfy = pd.DataFrame(boston.target, columns=["MEDV"])

독립변수과 종속변수 데이터프레임을 하나의 데이터프레임으로 묶어두면 편리하다.

df = pd.concat([dfX, dfy], axis=1)
df.tail()

	CRIM	INDUS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT	MEDV
501	0.06263	11.93	0.573	6.593	69.1	2.4786	1.0	273.0	21.0	391.99	9.67	22.4
502	0.04527	11.93	0.573	6.120	76.7	2.2875	1.0	273.0	21.0	396.90	9.08	20.6
503	0.06076	11.93	0.573	6.976	91.0	2.1675	1.0	273.0	21.0	396.90	5.64	23.9
504	0.10959	11.93	0.573	6.794	89.3	2.3889	1.0	273.0	21.0	393.45	6.48	22.0
505	0.04741	11.93	0.573	6.030	80.8	2.5050	1.0	273.0	21.0	396.90	7.88	11.9

일부 독립변수와 종속변수의 관계를 스캐터플롯(scatter plot)으로 살펴보자.

sns.pairplot(df[["MEDV", "RM", "AGE", "CHAS"]])
plt.show()

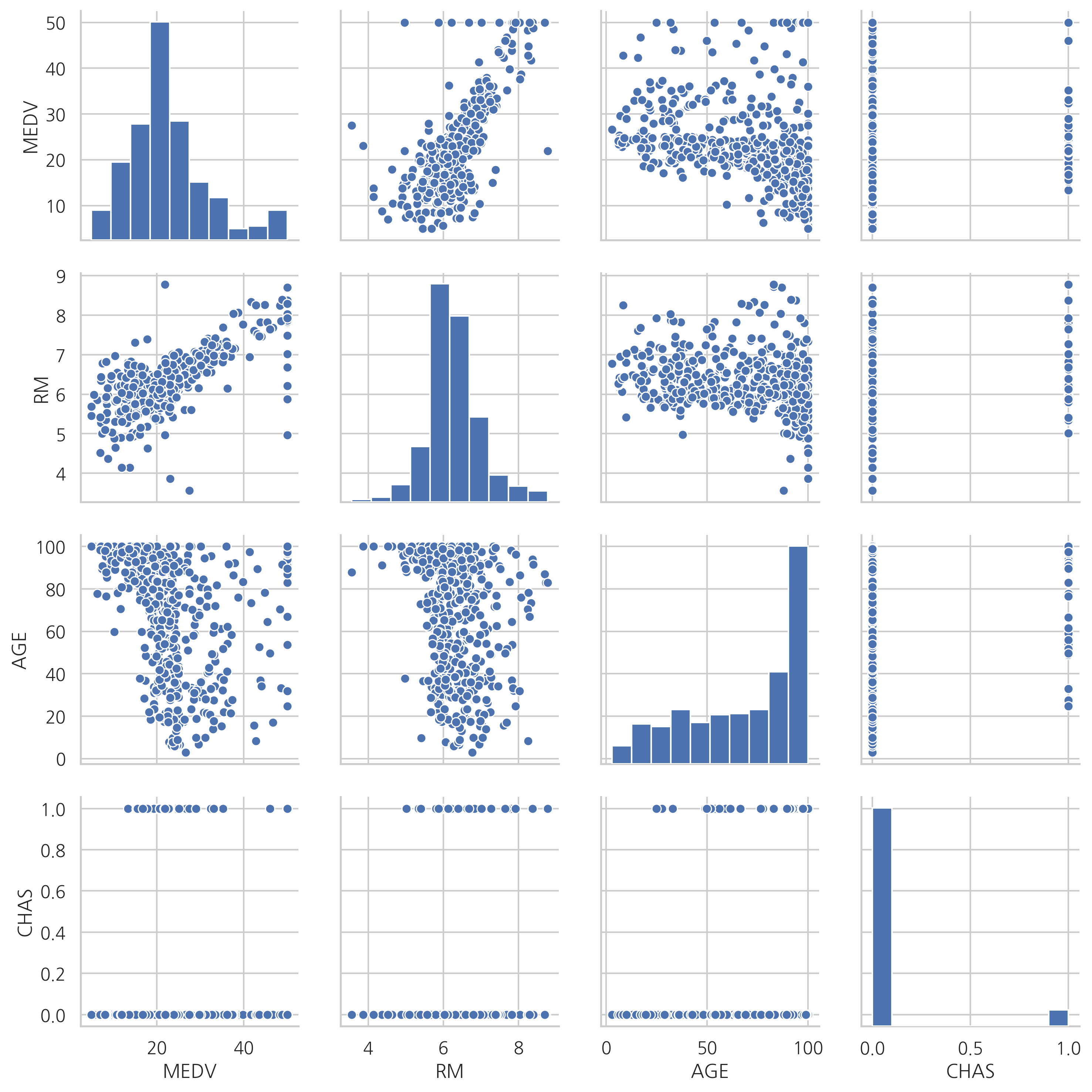
이 플롯의 첫 행을 보면 종속변수인 집값(MEDV)과 방 개수(RM), 노후화 정도(AGE)와 어떤 관계를 가지는지 알 수 있다.

방 개수가 증가할 수록 집값은 증가하는 경향이 뚜렷하다.
노후화 정도와 집값은 관계가 없어 보인다.

또한 스케터플롯의 모양으로부터 찰스강 유역 여부(CHAS)는 범주값이며 값이 1이면 0일 때 보다 집값의 평균이 더 높아지는 것도 볼 수 있다.

당뇨병 진행도 예측¶

scikit-learn 패키지가 제공하는 당뇨병 진행도 예측용 데이터는 442명의 당뇨병 환자를 대상으로한 검사 결과를 나타내는 데이터이다.

다음과 같은 10 종류의 독립변수를 가지고 있다. 독립변수의 값들은 모두 스케일링(scaling)되었다.

age: 나이
sex: 성별
bmi: BMI(Body mass index)지수
bp: 평균혈압
s1~s6: 6종류의 혈액검사수치

종속변수는 1년 뒤 측정한 당뇨병의 진행률이다.

from sklearn.datasets import load_diabetes

diabetes = load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
df["target"] = diabetes.target
df.tail()

	age	sex	bmi	bp	s1	s2	s3	s4	s5	s6	target
437	0.041708	0.050680	0.019662	0.059744	-0.005697	-0.002566	-0.028674	-0.002592	0.031193	0.007207	178.0
438	-0.005515	0.050680	-0.015906	-0.067642	0.049341	0.079165	-0.028674	0.034309	-0.018118	0.044485	104.0
439	0.041708	0.050680	-0.015906	0.017282	-0.037344	-0.013840	-0.024993	-0.011080	-0.046879	0.015491	132.0
440	-0.045472	-0.044642	0.039062	0.001215	0.016318	0.015283	-0.028674	0.026560	0.044528	-0.025930	220.0
441	-0.045472	-0.044642	-0.073030	-0.081414	0.083740	0.027809	0.173816	-0.039493	-0.004220	0.003064	57.0

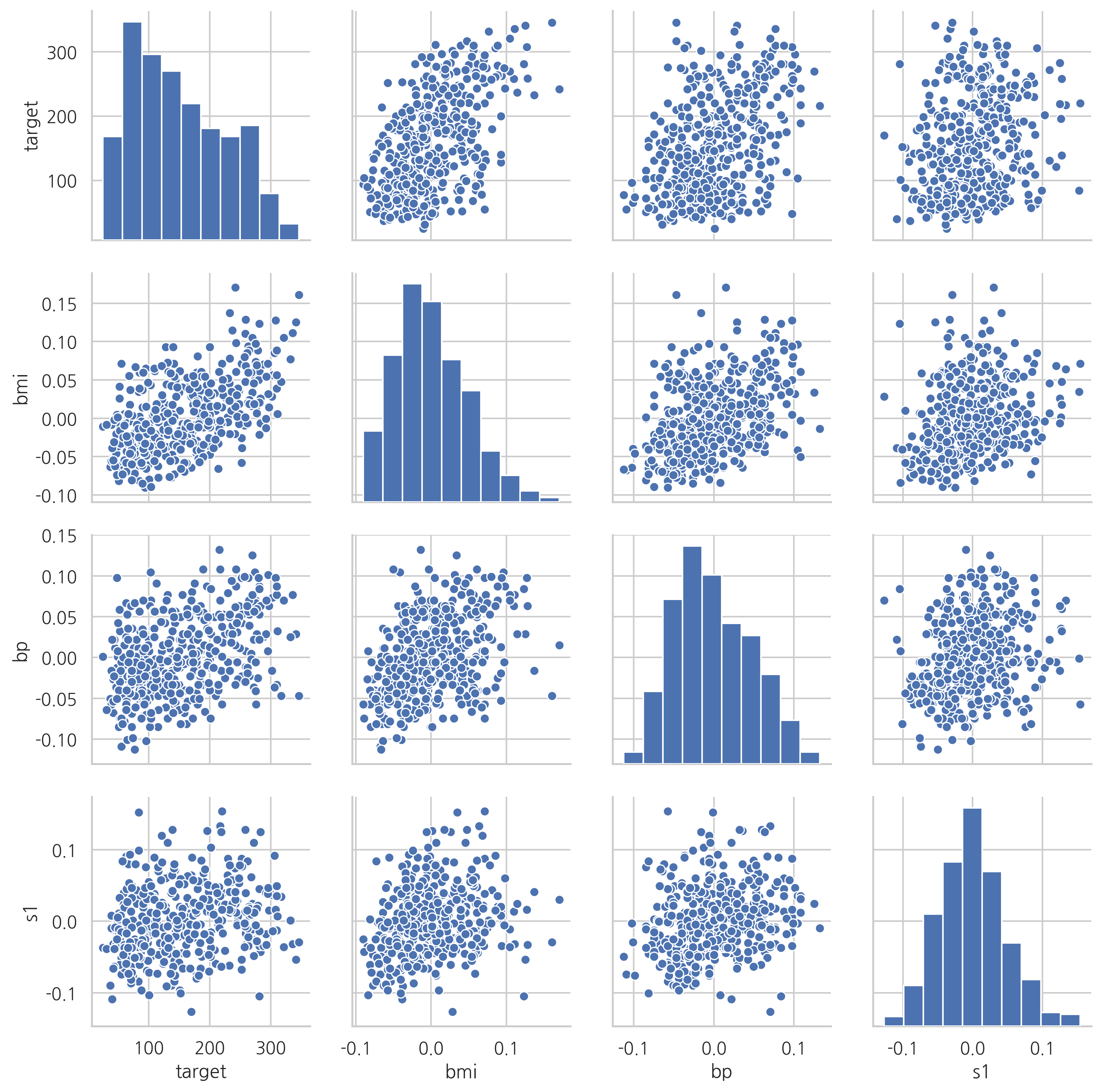
스케터플롯을 그려보면 독립변수인 BMI지수와 평균혈압이 종속변수인 당뇨병 진행도와 양의 상관관계를 가지는 것을 볼 수 있다. 또한 두 독립변수 BMI지수와 평균혈압도 서로 양의 상관관계를 가진다. 이렇게 독립변수끼리 상관관계를 가지는 것을 다중공선성(multicolinearity)이라고 한다. 다중공선성은 회귀분석의 결과에 영향을 미칠 수 있다.

sns.pairplot(df[["target", "bmi", "bp", "s1"]])
plt.show()

연습 문제 4.1.1¶

sklearn.datasets 패키지의 fetch_california_housing 명령은 캘리포니아 주택가격을 예측하기위한 데이터다. 이 데이터의 독립변수를 조사하고 어떤 데이터들이 주택가격과 상관관계가 있는지를 조사한다. 또한 서로 강한 상관관계를 가지는 독립변수도 알아보자.

가상 데이터 예측¶

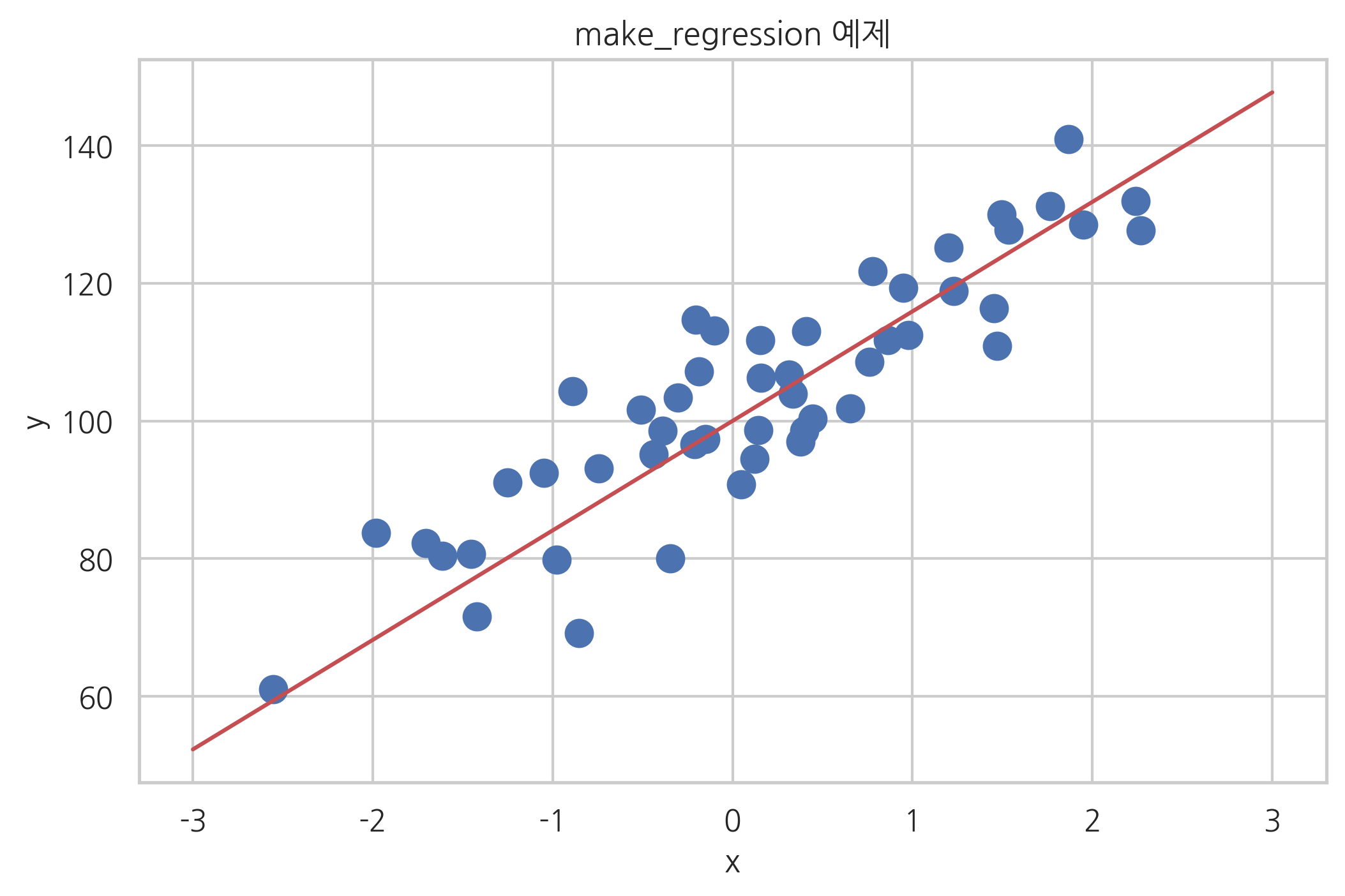
scikit-learn 패키지는 가상의 회귀분석 문제를 만들어주는 make_regression() 명령도 제공한다. 사용법은 다음과 같다.

X, y, w = make_regression(n_samples, n_features, bias, noise, random_state, coef=True)

n_samples : 정수 (옵션, 디폴트 100)
- 표본 데이터의 갯수 \(N\)
n_features : 정수 (옵션, 디폴트 100)
- 독립변수(feature)의 수(차원) \(M\)
bias : 실수 (옵션, 디폴트 0)
- y 절편
noise : 실수 (옵션, 디폴트 0)
- 출력 즉, 종속변수에 더해지는 잡음 \(\epsilon\)의 표준편차
random_state : 정수 (옵션, 디폴트 None)
- 난수 발생용 시드값
coef : 불리언 (옵션, 디폴트 False)
- True 이면 선형 모형의 계수도 출력

출력은 다음과 같다.

X : [n_samples, n_features] 형상의 2차원 배열
- 독립변수의 표본 데이터 행렬 \(X\)
y : [n_samples] 형상의 1차원 배열
- 종속변수의 표본 데이터 벡터 \(y\)
w : [n_features] 형상의 1차원 배열 또는 [n_features, n_targets] 형상의 2차원 배열 (옵션)
- 선형 모형의 계수 벡터 \(w\), 입력 인수 coef가 True 인 경우에만 출력됨

make_regression() 명령은 내부적으로 다음 과정을 거쳐 가상의 데이터를 만든다.

독립변수 데이터 행렬 X를 무작위로 만든다.
종속변수와 독립변수를 연결하는 가중치 벡터 w를 무작위로 만든다.
X와 w를 내적하고 y절편 b 값을 더하여 독립변수와 완전선형인 종속변수 벡터 y_0를 만든다.
기댓값이 0이고 표준편차가 noise인 정규분포를 이용하여 잡음 epsilon를 만든다.
독립변수와 완전선형인 종속변수 벡터 y_0에 잡음 epsilon을 더해서 종속변수 데이터 \(y\)를 만든다.

\[ y = w^Tx + b + \epsilon \]

from sklearn.datasets import make_regression

X, y, w = make_regression(
    n_samples=50, n_features=1, bias=100, noise=10, coef=True, random_state=0
)

xx = np.linspace(-3, 3, 100)
y0 = w * xx + 100
plt.plot(xx, y0, "r-")
plt.scatter(X, y, s=100)
plt.xlabel("x")
plt.ylabel("y")
plt.title("make_regression 예제")
plt.show()

연습 문제 4.1.2¶

make_regression과 같은 기능을 하는 함수 make_regression2를 만들어라. 단 make_regression2는 coef=True, n_features=1 라고 가정한다. 즉 항상 가중치 계수를 반환하고 1차원 독립변수만 생성할 수 있다. 따라서 make_regression2는 다음과 같은 인수만 가진다.

n_samples
bias
noise
random_state

따라서 함수 사용법은 다음과 같아야 한다.

X, y, w = make_regression2(n_samples, bias, noise, random_state)

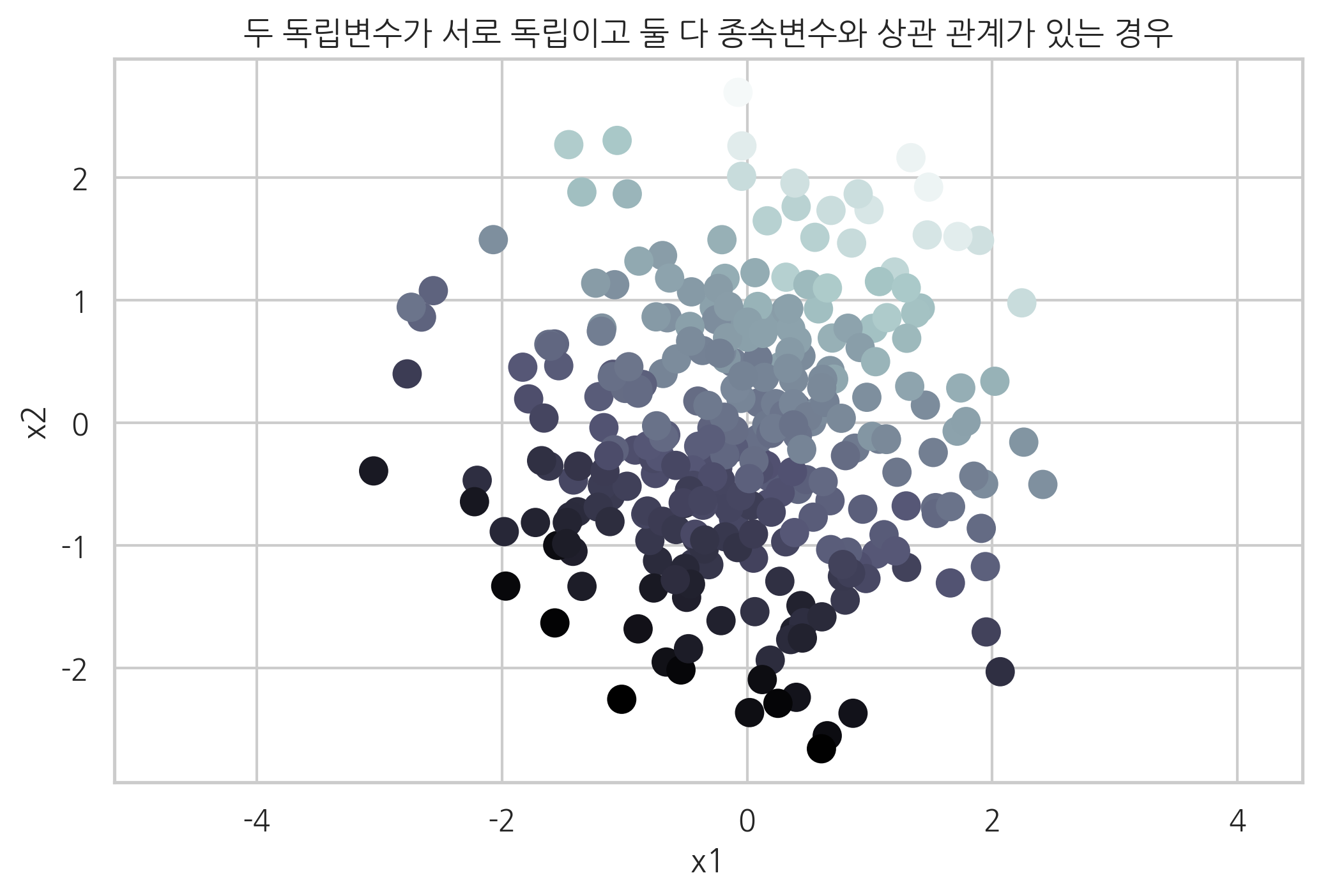
독립변수가 2개인 표본 데이터를 생성하여 스캐터플롯을 그리면 다음과 같다. 종속변숫값은 점의 명암으로 표시하였다. 점의 밝기가 밝으면 종속변숫값이 큰 것이고 점의 밝기가 어두우면 종속변숫값이 작은것이다. 스캐터플롯에서 x1, x2가 증가할수록 종속변숫값이 커지는 것을 알 수 있다.

X, y, w = make_regression(
    n_samples=300, n_features=2, noise=10, coef=True, random_state=0
)

plt.scatter(X[:, 0], X[:, 1], c=y, s=100, cmap=mpl.cm.bone)
plt.xlabel("x1")
plt.ylabel("x2")
plt.axis("equal")
plt.title("두 독립변수가 서로 독립이고 둘 다 종속변수와 상관 관계가 있는 경우")
plt.show()

make_regression 명령은 위에서 설명한 인수 이외에도 다음과 같은 인수를 가질 수 있다.

n_informative : 정수 (옵션, 디폴트 10)
- 독립변수(feature) 중 실제로 종속변수와 상관 관계가 있는 독립변수의 수(차원)
effective_rank: 정수 또는 None (옵션, 디폴트 None)
- 독립변수(feature) 중 서로 독립인 독립변수의 수. 만약 None이면 모두 독립
tail_strength : 0부터 1사이의 실수 (옵션, 디폴트 0.5)
- effective_rank가 None이 아닌 경우 독립변수간의 상관관계를 결정하는 변수. 0.5면 독립변수간의 상관관계가 없다.

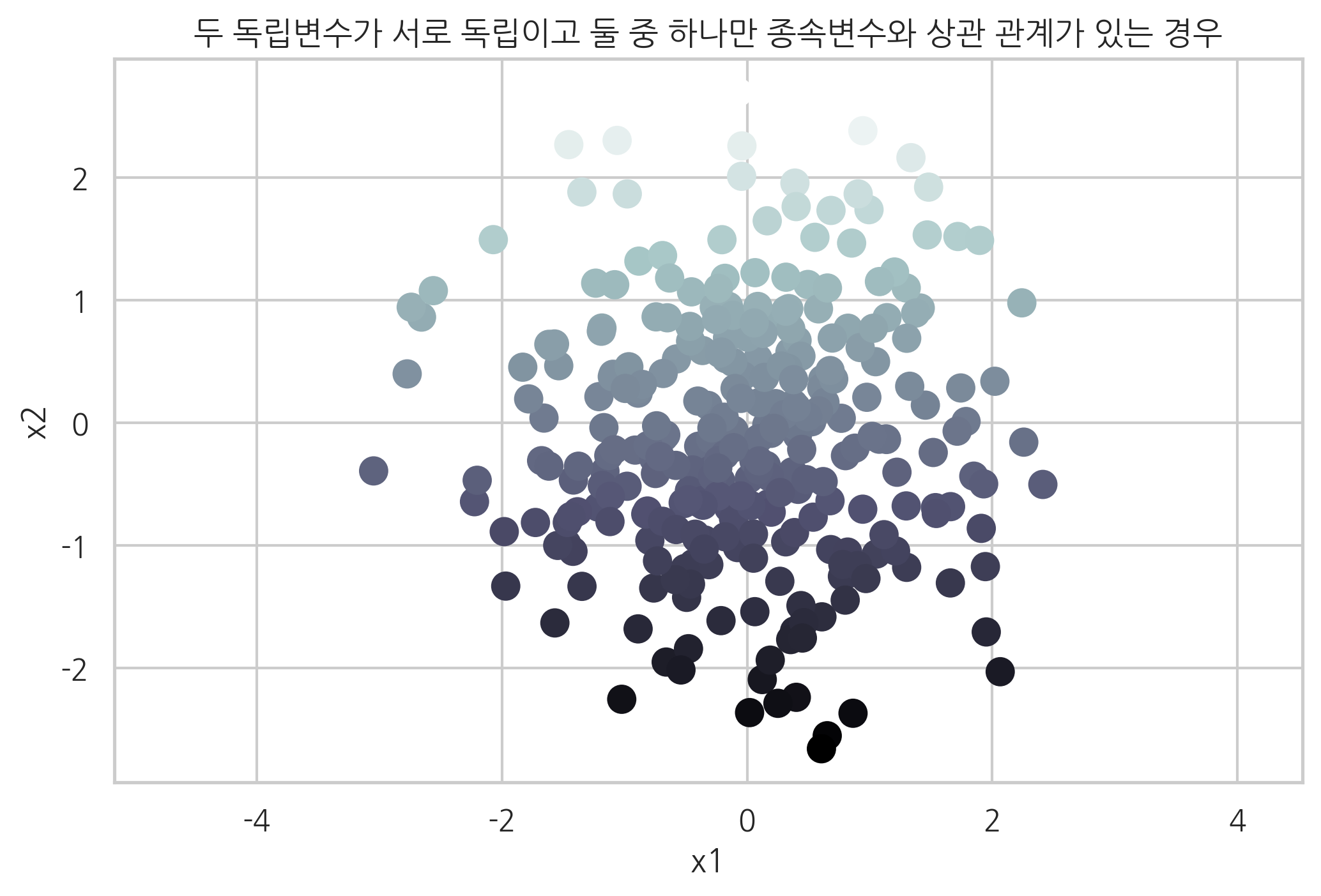
예를 들어 두 독립변수 중 실제로 종속변수에 영향을 미치는 독립변수는 하나 뿐이라면 다음처럼 n_informative=1로 설정한다. 스캐터플롯에서 독립변수 x1은 종속변수에 영향을 미치지 않는 것을 알 수 있다.

X, y, w = make_regression(
    n_samples=300, n_features=2, n_informative=1, noise=0, coef=True, random_state=0
)

plt.scatter(X[:, 0], X[:, 1], c=y, s=100, cmap=mpl.cm.bone)
plt.xlabel("x1")
plt.ylabel("x2")
plt.axis("equal")
plt.title("두 독립변수가 서로 독립이고 둘 중 하나만 종속변수와 상관 관계가 있는 경우")
plt.show()

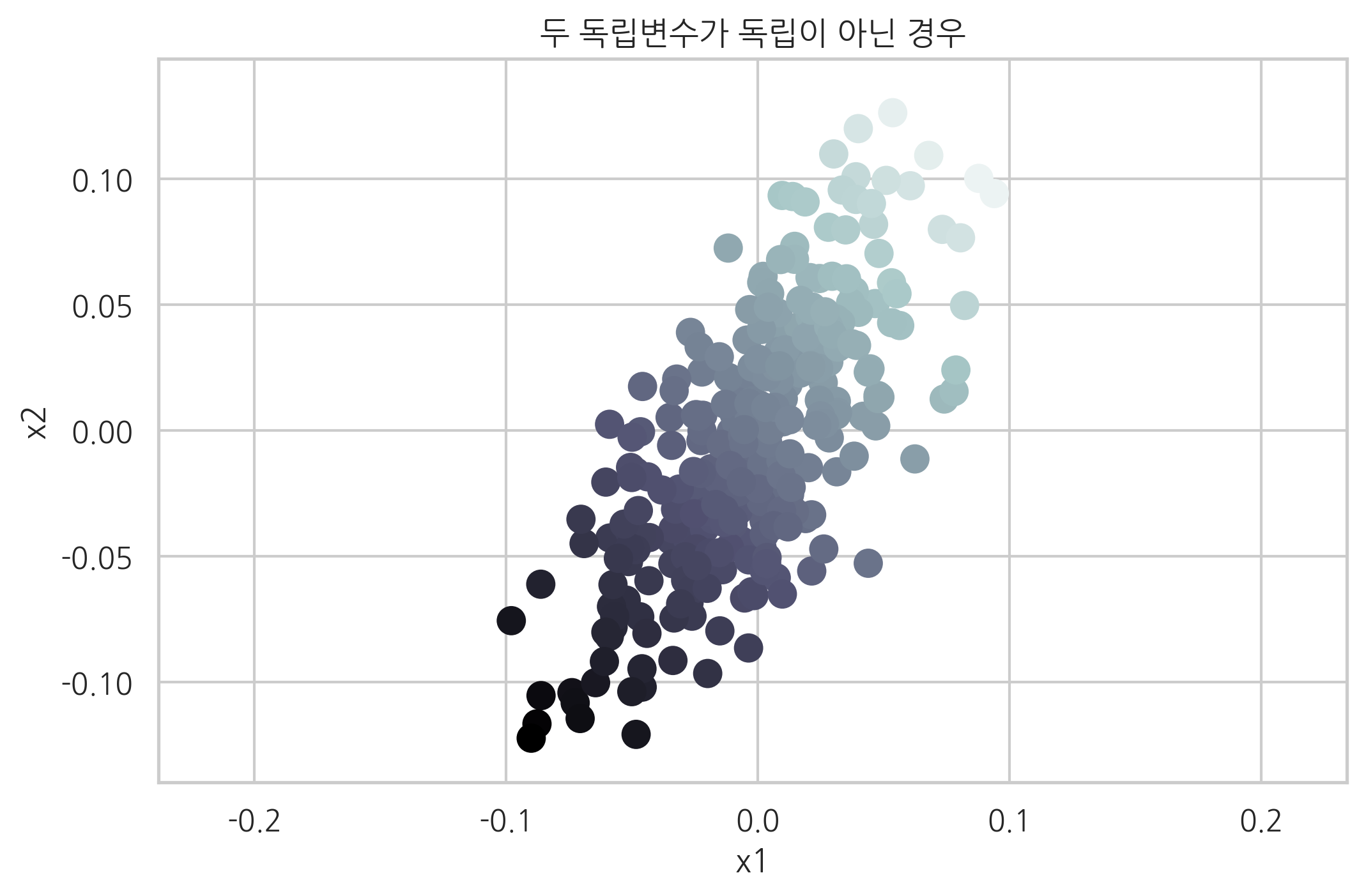
만약 두 독립변수가 서로 독립이 아니고 상관관계를 가지는 다중공선성 데이터를 만드는 경우에는 tail_strength 인수를 0에 가까운 작은 값으로 설정한다.

X, y, w = make_regression(
    n_samples=300, n_features=2, effective_rank=1, noise=0, coef=True, random_state=0,
    tail_strength=0
)

plt.scatter(X[:, 0], X[:, 1], c=y, s=100, cmap=mpl.cm.bone)
plt.xlabel("x1")
plt.ylabel("x2")
plt.axis("equal")
plt.title("두 독립변수가 독립이 아닌 경우")
plt.show()

데이터 사이언스 스쿨