8.1 사이파이를 이용한 확률분포 분석

사이파이(SciPy)는 수치해석기능을 제공하는 파이썬 패키지다. 여러 서브패키지로 구성되어 있는데 그중 stats 서브패키지는 확률분포 분석을 위한 다양한 기능을 제공한다. 다음 코드로 임포트한다.

import scipy as sp
import scipy.stats

확률분포 클래스

사이파이에서 확률분포 기능을 사용하려면 우선 해당 확률분포에 대한 확률분포 클래스 객체를 생성한 후에 이 객체의 메서드를 호출해야 한다.

확률분포 객체를 생성하는 명령에는 다음과 같은 것들이 있다.

종류	명령	확률분포
이산	bernoulli	베르누이분포
이산	binom	이항분포
이산	multinomial	다항분포
연속	uniform	균일분포
연속	norm	정규분포
연속	beta	베타분포
연속	gamma	감마분포
연속	t	스튜던트 t분포
연속	chi2	카이 제곱분포
연속	f	F분포
연속	dirichlet	디리클리분포
연속	multivariate_normal	다변수 정규분포

이 명령들은 모두 stats 서브패키지에 포함되어 있다. 예를 들어 정규분포 객체는 다음과 같이 생성한다.

rv = sp.stats.norm()

모수 지정

확률분포 객체를 생성할 때는 분포의 형상을 구체적으로 지정하는 **모수(parameter)**를 인수로 주어야 한다. 각 확률분포마다 설정할 모수가 다르므로 자세한 설명은 사이파이 문서를 참조한다. 하지만 대부분 다음과 같은 모수를 공통적으로 가진다.

인수(모수) 이름	의미
loc	일반적으로 분포의 기댓값
scale	일반적으로 분포의 표준편차

예를 들어 기댓값이 1이고 표준 편차가 2인 정규분포 객체는 다음과 같이 생성한다.

rv = sp.stats.norm(loc=1, scale=2)

확률분포 메서드

확률분포 객체가 가지는 메서드는 다음과 같다.

메서드	기능
pmf	확률질량함수(probability mass function)
pdf	확률밀도함수(probability density function)
cdf	누적분포함수(cumulative distribution function)
ppf	누적분포함수의 역함수(inverse cumulative distribution function)
sf	생존함수(survival function) = 1 - 누적분포함수
isf	생존함수의 역함수(inverse survival function)
rvs	랜덤 표본 생성(random variable sampling)

각 메서드 사용법은 다음과 같다.

확률밀도함수

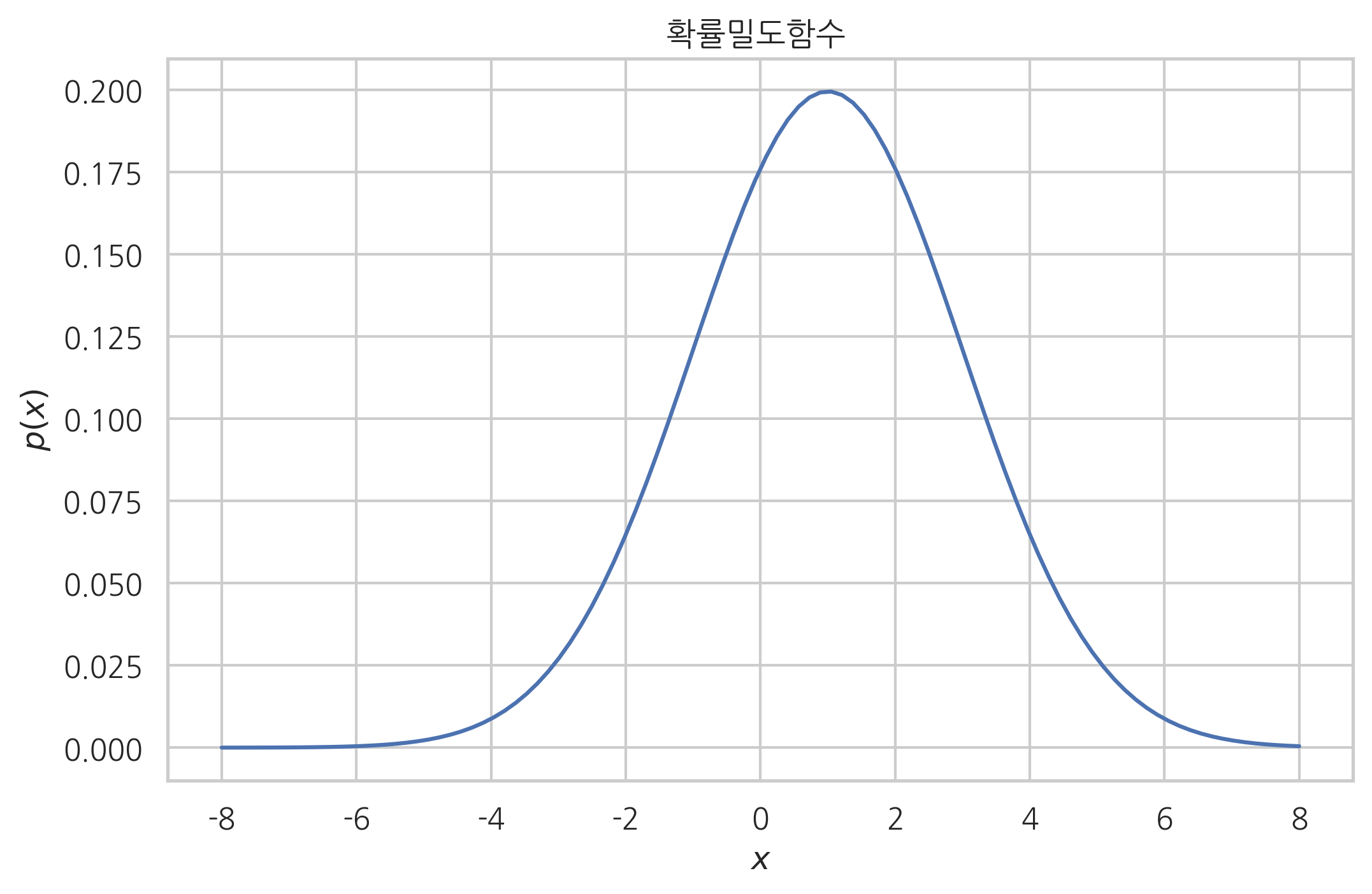
pdf 메서드는 연속확률변수의 확률밀도함수의 역할을 한다. 표본 값을 입력하면 해당 표본 값에 대한 확률밀도를 출력한다.

xx = np.linspace(-8, 8, 100)
pdf = rv.pdf(xx)
plt.plot(xx, pdf)
plt.title("확률밀도함수 ")
plt.xlabel("$x$")
plt.ylabel("$p(x)$")
plt.show()

연습 문제 8.1.1

(1) 기댓값이 0이고 표준 편차가 0.1인 정규분포의 객체를 만들고 확률밀도함수를 그려라.

(2) 이 확률밀도함수의 최대값은 얼마인가?

누적분포함수

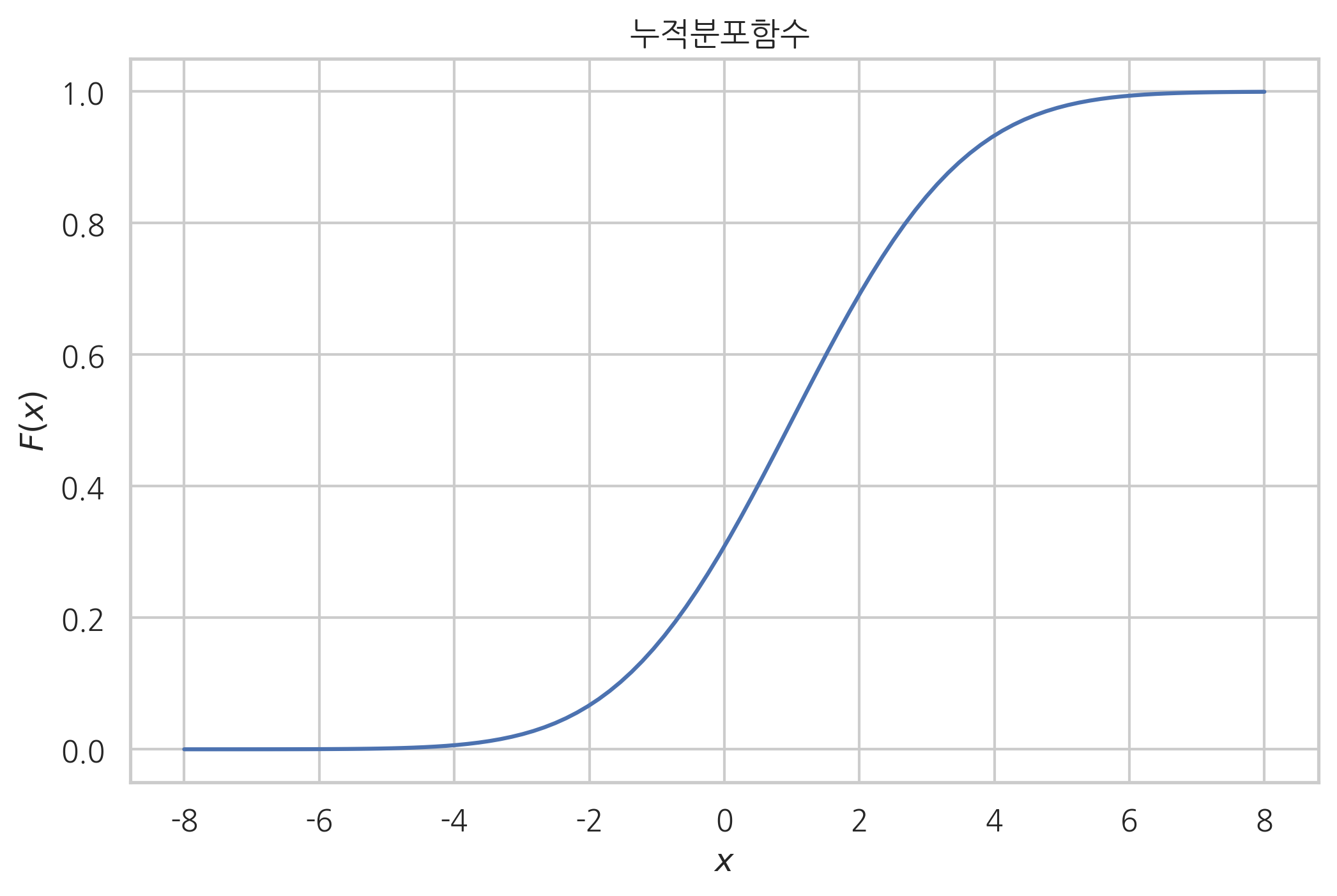
cdf 메서드는 이산확률변수와 연속확률변수의 누적분포함수의 역할을 한다. 표본 값을 입력하면 해당 표본 값에 대한 누적확률을 출력한다.

xx = np.linspace(-8, 8, 100)
cdf = rv.cdf(xx)
plt.plot(xx, cdf)
plt.title("누적분포함수 ")
plt.xlabel("$x$")
plt.ylabel("$F(x)$")
plt.show()

무작위 표본 생성

무작위로 표본을 만들 때는 rvs(random value sampling) 메서드를 사용한다. 이 메서드에서 받는 인수는 다음과 같다.

인수	의미
size	표본 생성 시 생성될 표본 크기
random_state	표본 생성 시 사용되는 시드(seed)값

rv.rvs(size=(3, 5), random_state=0)

array([[ 4.52810469,  1.80031442,  2.95747597,  5.4817864 ,  4.73511598],
       [-0.95455576,  2.90017684,  0.69728558,  0.7935623 ,  1.821197  ],
       [ 1.28808714,  3.90854701,  2.52207545,  1.24335003,  1.88772647]])

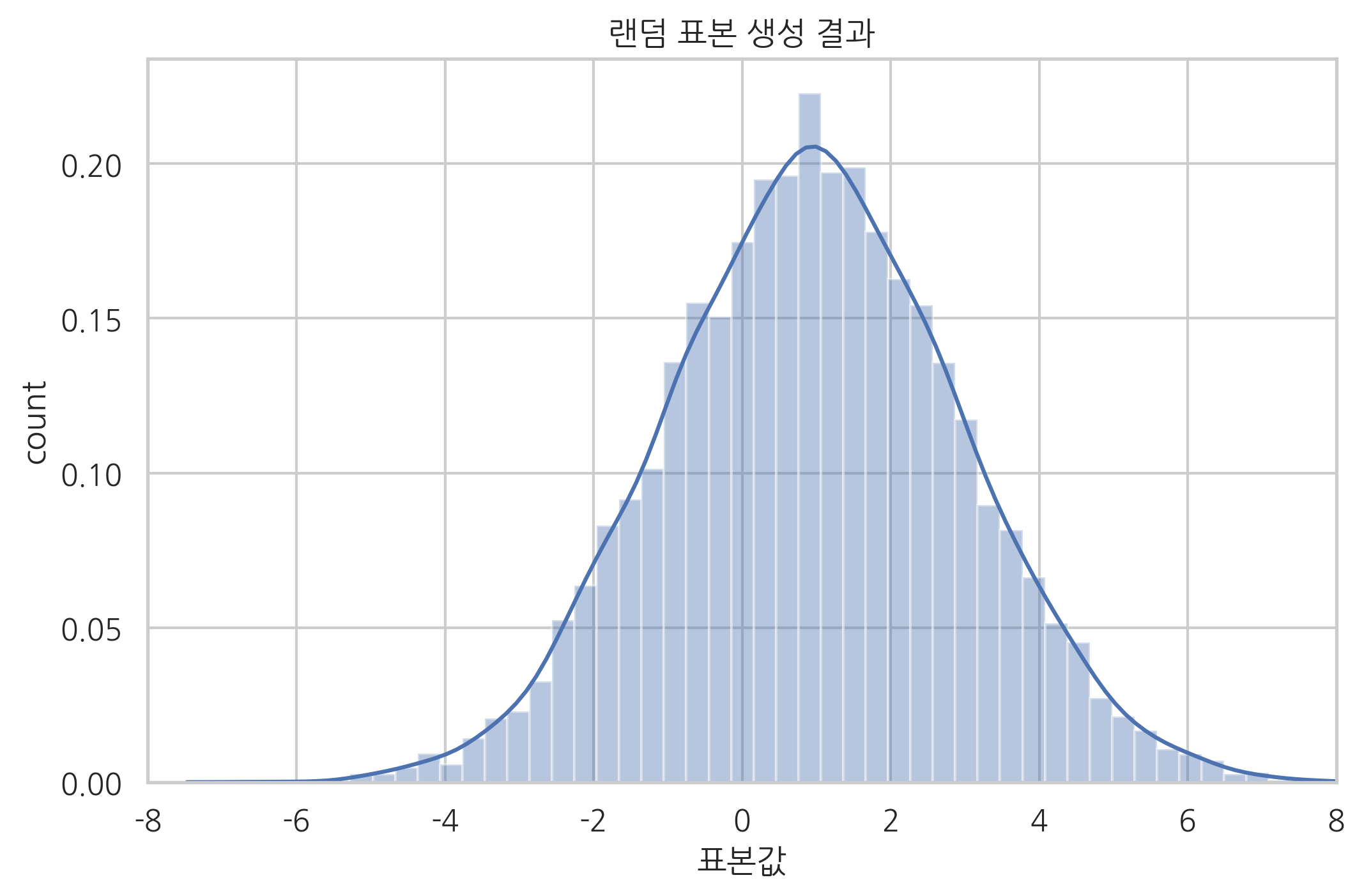
sns.distplot(rv.rvs(size=10000, random_state=0))
plt.title("랜덤 표본 생성 결과")
plt.xlabel("표본값")
plt.ylabel("count")
plt.xlim(-8, 8)
plt.show()

연습 문제 8.1.2

rvs 명령으로 1000개의 정규분포의 표본 데이터를 생성하고 이 표본 데이터로부터 표본평균과 비편향 표본분산을 계산하라. 이 값이 인수로 넣은 기댓값과 분산과 비슷한지 비교하라.

변환 확률변수의 시뮬레이션

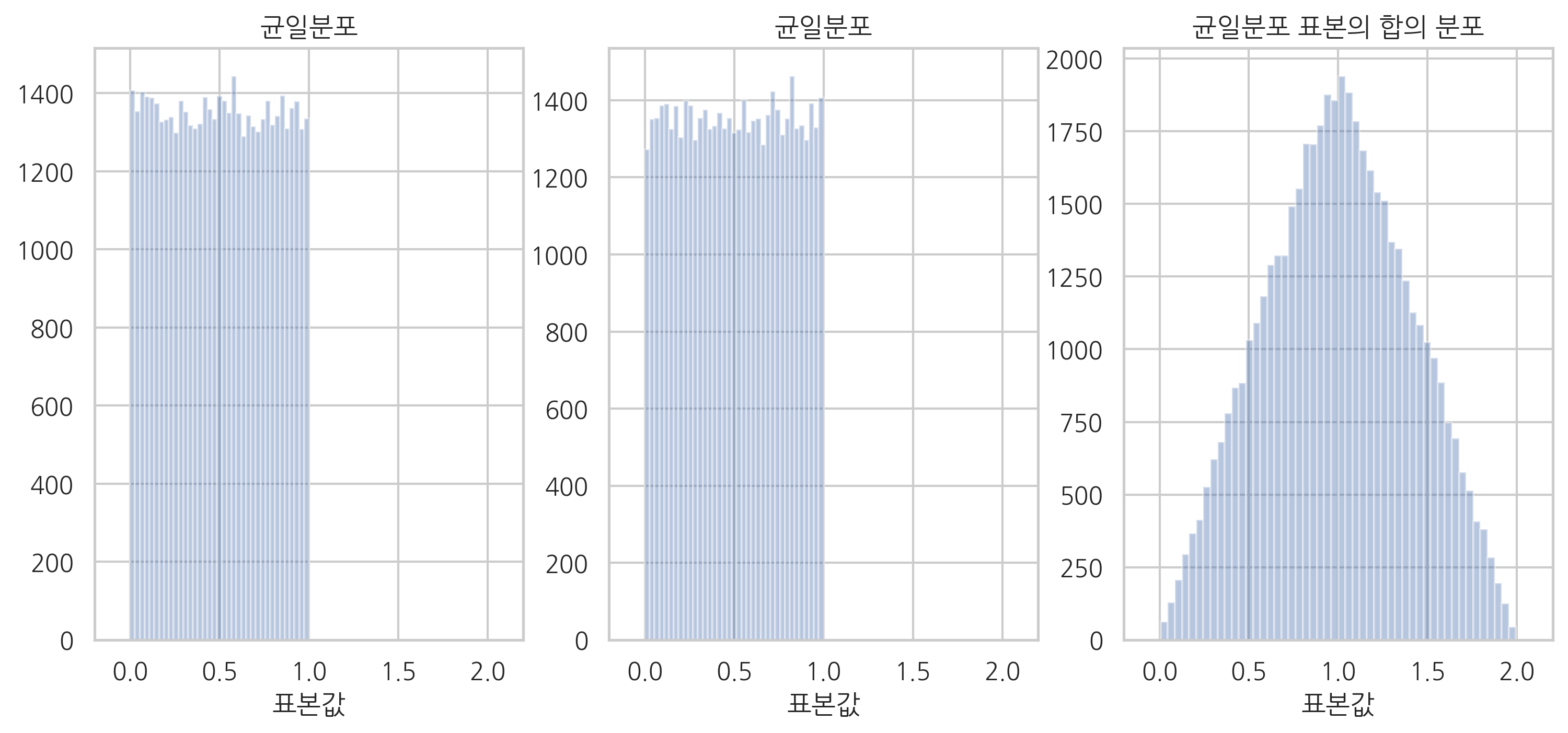
시뮬레이션 기능을 사용하면 확률변수의 표본을 가공하여 만들어진 변환(transform) 확률변수의 확률분포도 알 수 있다. 예를 들어 0과 1 사이의 균일분포를 가지는 확률변수에서 두 표본값을 생성하여 이 두 값을 합하면 결과는 어떤 분포를 가질까? 얼핏 생각하듯이 균일분포에서 나온 두 표본값의 합은 균일분포가 되지 않는다. 시뮬레이션으로 확인하면 1에서 최빈값을 가지는 삼각형 모양의 분포가 된다는 것을 알 수 있다.

rv1 = sp.stats.uniform()
rv2 = sp.stats.uniform()

np.random.seed(0)
N = 50000
x_1 = rv1.rvs(N)
x_2 = rv2.rvs(N)
x_3 = x_1 + x_2

plt.figure(figsize=(12, 5))

plt.subplot(131)
sns.distplot(x_1, kde=False)
plt.title("균일분포")
plt.xlabel("표본값")
plt.xlim(-0.2, 2.2)

plt.subplot(132)
sns.distplot(x_2, kde=False)
plt.title("균일분포")
plt.xlabel("표본값")
plt.xlim(-0.2, 2.2)

plt.subplot(133)
sns.distplot(x_3, kde=False)
plt.title("균일분포 표본의 합의 분포")
plt.xlabel("표본값")
plt.xlim(-0.2, 2.2)

plt.show()

연습 문제 8.1.3

균일분포 확률분포에서 두 개가 아닌 10개 표본값을 생성하여 그 값의 합을 구하면 어떤 모양의 분포를 이루는지 시뮬레이션 기능을 사용하여 구하라. 이 때 시뮬레이션은 1000번 반복한다.