5.2 회귀분석의 기하학#
회귀 벡터공간#
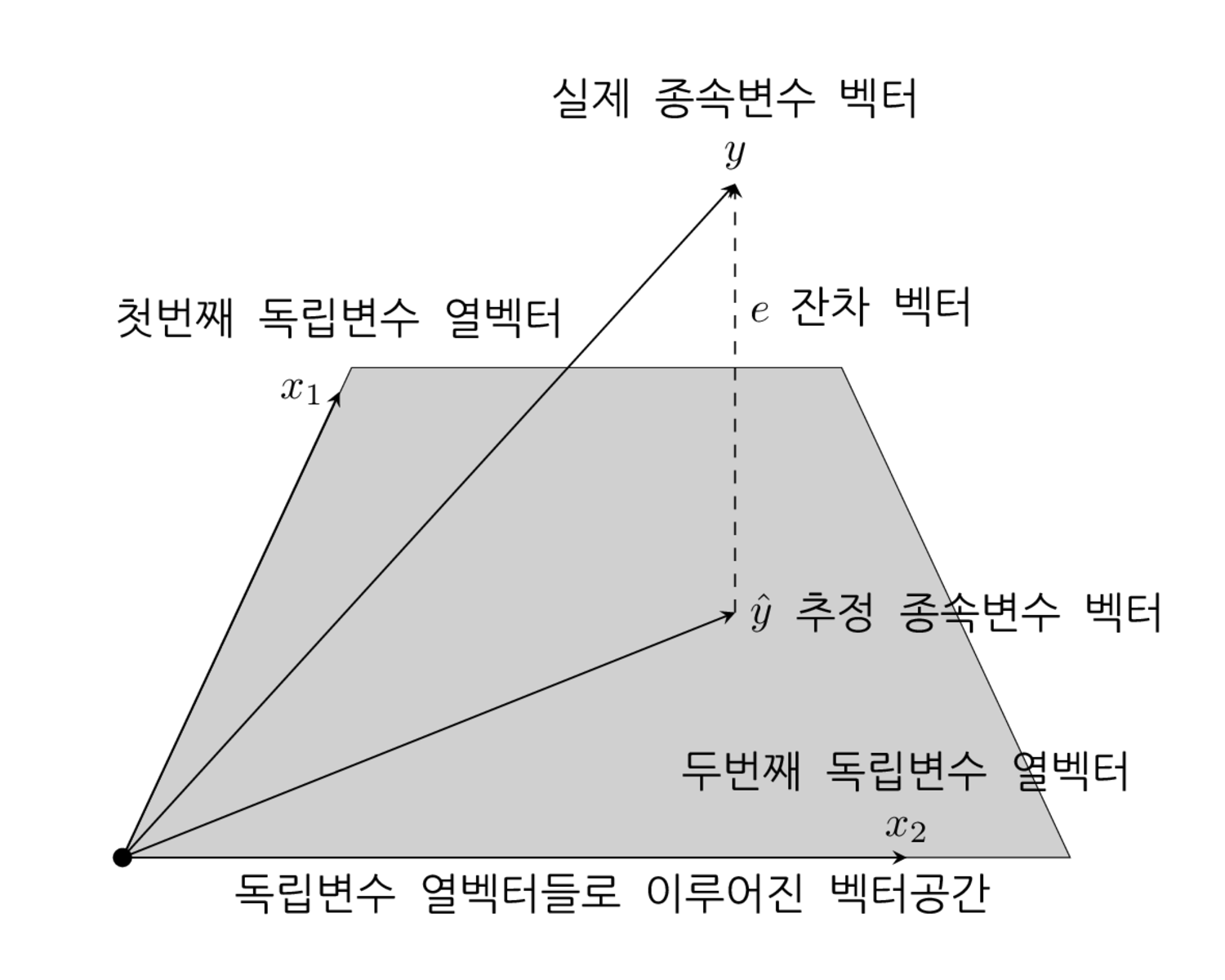
선형 회귀분석으로 예측한 값 \(\hat{y}\)는 \(X\)의 각 열 \(c_1, \cdots, c_M\)의 선형조합으로 표현된다.
모든 열이 선형독립이면 예측값 \(\hat{y}\)는 \(X\)의 각 열 \(c_1, \cdots, c_M\)을 기저벡터(basis vector)로 하는 벡터공간(vector space)위에 존재한다는 것을 알 수 있다.
실제 종속변수 데이터 \(y\)와 예측값 \(\hat{y}\)의 차이가 잔차 벡터 \(e\)이다. 따라서 잔차 벡터 \(e\)의 크기를 가장 작게 만드는 최적의 예측값 \(\hat{y}\)는 벡터공간내에 존재하면서 \(y\)와 가장 가까운 벡터이다. 이 때 잔차 벡터 \(e\)는 벡터 공간에 직교한다. 따라서 예측값 벡터 \(\hat{y}\)는 \(y\)를 \(X\)의 각 열 \(c_1, \cdots, c_M\)을 기저벡터로 하는 벡터공간에 투영(projection)한 벡터이고 잔차 벡터 \(e\)는 투영하고 남은 직교 벡터이다.
%load_ext tikzmagic
%%tikz -p kotex,pgfplots,pgffor -l arrows.meta,calc,positioning,shapes -s 2000,1200 -f png
\coordinate (leftbottom) at (-1,-1);
\coordinate (righttop) at (9,7);
\fill[white,use as bounding box] (leftbottom) rectangle (righttop);
\draw[help lines,white] (leftbottom) grid (righttop);
\tikzset{
>=stealth,font={\ttfamily}
}
\tikzstyle{channel}=[trapezium, draw, shape border uses incircle, minimum size=4cm,
trapezium left angle=65, trapezium right angle=65]
\node[channel,fill=darkgray!30,draw=black,xshift=3.87cm,yshift=2cm, line width=0.2] at (0,0) (background) {};
\coordinate (origin) at (0,0,0);
\draw[fill] (origin) circle (2pt);
\draw [->] (origin) -- (1.77,3.8,0) coordinate (x1) node[left] {$\small{x_1}$};
\node at ($(x1)+(0,0.6)$) {첫번째 독립변수 열벡터};
\draw [->] (origin) -- (6.4,0,0) coordinate (x2) node[above] {$x_2$};
\node at ($(x2)+(0,0.7)$) {두번째 독립변수 열벡터};
\draw [->] (origin) -- (5,5.5,0) coordinate (y) node[above] {$y$};
\node at ($(y)+(0,0.7)$) {실제 종속변수 벡터};
\draw [->] (origin) -- (5,2,0) coordinate (y_h) node[right] {$\hat{y}$};
\node at ($(y_h)+(2,0)$) {추정 종속변수 벡터};
\draw [->,dashed] (5,2,0) -- (5,5.5,0) coordinate (e) node[pos=0.7,right] {$e$};
\node at ($(e)+(1.2,-1)$) {잔차 벡터};
\node at (4,-0.3) {독립변수 열벡터들로 이루어진 벡터공간};
잔차행렬과 투영행렬#
벡터 \(a\)에서 다른 벡터 \(b\)를 변형하는 과정은 변형행렬(transforma matrix) \(T\)를 곱하는 연산으로 나타낼 수 있다.
종속값 벡터 \(y\)를 잔차 벡터 \(e\)로 변형하는 변환 행렬 \(M\)를 정의하자. 이 행렬을 **잔차행렬(residual matrix)**이라고 한다.
종속값 벡터 \(y\)를 예측값 벡터 \(\hat{y}\)로 변형하는 변환 행렬 \(H\)를 정의하자.. 이 행렬을 **투영행렬(projection matrix)**이라고 한다.
잔차행렬은 다음과 같이 구한다.
투영행렬은 다음과 같이 구한다.
따라서 \(M\), \(H\)는 각각 다음과 같다.
투영 행렬은 y로부터 \(\hat{}\)기호가 붙은 \(\hat{y}\)를 계산한다고 해서 햇(hat) 행렬 또는 **영향도 행렬(influence matrix)**이라고 부르기도 한다. 영향도 행렬이라는 명칭의 의미는 아웃라이어 분석에서 다시 다룬다.
잔차 행렬과 투영 행렬은 다음과 같은 성질이 있다.
(1) 대칭행렬이다.
(2) 곱해도 자기 자신이 되는 행렬이다. 이러한 행렬을 멱등(idempotent)행렬이라고 한다. 멱등행렬은 몇번을 곱해도 자기 자신이 된다.
(3) \(M\)과 \(H\)는 서로 직교한다.
(4) \(M\)은 \(X\)와 직교한다.
(5) \(X\)에 \(H\)를 곱해도 변하지 않는다.
위 성질은 다음과 같이 증명한다.
(1) 대칭행렬의 증명
(2) 멱등성 증명
(3) \(M\)과 \(H\)의 직교 증명
(4) \(M\)과 \(X\)의 직교 증명
(5) \(H\)과 \(X\)의 곱에 대한 증명
위 성질들을 이용하면 \(y\) 벡터의 제곱합은 잔차 벡터 \(e\)의 제곱합과 추정치 벡터 \(\hat{y}\)의 제곱합의 합이라는 것을 알 수 있다.
이 관계식은 나중에 분산 분석(ANOVA)에 사용된다.