4.4 행렬의 미분
지금까지는 스칼라값을 입력으로 받아 스칼라값을 출력하는 함수를 생각했다. 이제부터는 벡터나 행렬을 입력으로 받아서 벡터나 행렬을 출력하는 함수를 살펴본다.
여러개의 입력을 가지는 다변수 함수는 함수의 독립변수가 벡터인 경우로 볼 수 있다.
\[\begin{split}
\begin{align}
f\left( \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \right) = f(x) = f(x_1, x_2)
\tag{4.4.1}
\end{align}
\end{split}\]
\[
\begin{align}
\text{vector } x \;\; \rightarrow \;\; \text{scalar } f
\tag{4.4.2}
\end{align}
\]
이를 확장하면 행렬을 입력으로 가지는 함수도 생각할 수 있다.
\[\begin{split}
\begin{align}
f\left( \begin{bmatrix} x_{11} & x_{12} \\ x_{21} & x_{22} \end{bmatrix} \right)
= f(X) = f(x_{11}, \cdots, x_{22})
\tag{4.4.3}
\end{align}
\end{split}\]
\[
\begin{align}
\text{matrix } x \;\; \rightarrow \;\; \text{scalar } f
\tag{4.4.4}
\end{align}
\]
반대로 벡터나 행렬을 출력하는 함수는 여러개의 함수를 합쳐놓은 것이다.
\[\begin{split}
\begin{align}
f(x) =
\begin{bmatrix}
f_1(x) \\
f_2(x)
\end{bmatrix}
\tag{4.4.5}
\end{align}
\end{split}\]
\[
\begin{align}
\text{scalar } x \;\; \rightarrow \;\; \text{vector } f
\tag{4.4.6}
\end{align}
\]
\[\begin{split}
\begin{align}
f(x) =
\begin{bmatrix}
f_{11}(x) & f_{12}(x) \\
f_{21}(x) & f_{22}(x)
\end{bmatrix}
\tag{4.4.7}
\end{align}
\end{split}\]
\[
\begin{align}
\text{scalar } x \;\; \rightarrow \;\; \text{matrix } f
\tag{4.4.8}
\end{align}
\]
벡터나 행렬을 입력받아 벡터나 행렬을 출력할 수도 있다.
\[\begin{split}
\begin{align}
f(x) =
\begin{bmatrix}
f_1(x_1, x_2) \\
f_2(x_1, x_2)
\end{bmatrix}
\tag{4.4.9}
\end{align}
\end{split}\]
\[
\begin{align}
\text{vector } x \;\; \rightarrow \;\; \text{vector } f
\tag{4.4.10}
\end{align}
\]
\[\begin{split}
\begin{align}
f(x) =
\begin{bmatrix}
f_{11}(x_1, x_2) & f_{12}(x_1, x_2) \\
f_{21}(x_1, x_2) & f_{22}(x_1, x_2)
\end{bmatrix}
\tag{4.4.11}
\end{align}
\end{split}\]
\[
\begin{align}
\text{vector } x \;\; \rightarrow \;\; \text{matrix } f
\tag{4.4.12}
\end{align}
\]
이러한 행렬을 입력이나 출력으로 가지는 함수를 미분하는 것을 **행렬미분(matrix differentiation)**이라고 한다. 사실 행렬미분은 정확하게는 미분이 아닌 편미분(partial derivative)이지만 여기에서는 편의상 미분이라고 쓰겠다. 또한 행렬미분에는 분자중심 표현법(Numerator-layout notation)과 분모중심 표현법(Denominator-layout notation) 두 가지가 있는데 여기에서는 분모중심 표현법으로 서술한다.
스칼라를 벡터로 미분하는 경우
데이터 분석에서는 함수의 출력변수가 스칼라이고 입력변수 \(x\)가 벡터인 다변수 함수를 사용하는 경우가 많다. 따라서 편미분도 \(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots\) 등으로 여러 개가 존재한다.
이렇게 스칼라를 벡터로 미분하는 경우에는 결과를 열벡터로 표시한다. 이렇게 만들어진 벡터를 **그레디언트 벡터(gradient vector)**라고 하고 \(\nabla f\)로 표기한다.
\[\begin{split}
\begin{align}
\nabla f =
\frac{\partial f}{\partial {x}} =
\begin{bmatrix}
\dfrac{\partial f}{\partial x_1}\\
\dfrac{\partial f}{\partial x_2}\\
\vdots\\
\dfrac{\partial f}{\partial x_N}\\
\end{bmatrix}
\tag{4.4.13}
\end{align}
\end{split}\]
예제
다음과 같은 다변수 함수
\[
\begin{align}
f(x, y) = 2x^2 + 6xy + 7y^2 - 26x - 54y + 107
\tag{4.4.14}
\end{align}
\]
에 대한 그레디언트 벡터를 구하면
\[\begin{split}
\begin{align}
\nabla f =
\begin{bmatrix}
\dfrac{\partial f}{\partial x}\\
\dfrac{\partial f}{\partial y}\\
\end{bmatrix} =
\begin{bmatrix}
4x + 6y - 26\\
6x + 14y - 54\\
\end{bmatrix}
\tag{4.4.15}
\end{align}
\end{split}\]
가 된다.
연습 문제 4.4.1
다음 함수의 그레디언트 벡터를 구하라
(1)
$\(
\begin{align}
f(x, y, z) = x + y + z
\tag{4.4.16}
\end{align}
\)$
(2)
$\(
\begin{align}
f(x, y, z) = xyz
\tag{4.4.17}
\end{align}
\)$
연습 문제 4.4.2
그레디언트 벡터
\[\begin{split}
\begin{align}
\nabla f =
\begin{bmatrix}
4x + 6y - 26\\
6x + 14y - 54\\
\end{bmatrix}
\tag{4.4.18}
\end{align}
\end{split}\]
에 대해서 \(x, y\)가 다음 위치일 때 그레디언트 벡터의 값을 구하고 평면상에 화살표로 나타내라.
(1) \(x=7, y=1\)
(2) \(x=2, y=1\)
2차원의 경우를 예로 들어 그레디언트 벡터를 표시하는 법을 알아보자. 2개의 입력변수를 가지는 2차원 함수 \(f(x, y)\)는 평면상에서 컨투어(contour)플롯으로 나타낼 수 있다. 그리고 입력 변수 \(x, y\) 위치에서의 그레디언트 벡터 \(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\)는 그 위치를 원점으로 하는 화살표로 표현할 수 있다. 그리고 그레디언트 벡터의 방향은 편미분 성분 \(\frac{\partial f}{\partial x}\)와 \(\frac{\partial f}{\partial y}\)의 부호에 의해 결정된다.
만약 어떤 위치 \(x, y\)에서 \(x\)가 증가할수록 \(f\)가 커지면 도함수 \(\frac{\partial f}{\partial x}\)은 양수이다. 반대로 \(y\)가 증가할수록 \(f\)가 작아지면 도함수 \(\frac{\partial f}{\partial x}\)은 음수이다. 벡터는 2차원 평면에서 화살표로 나타낼 수 있다. 가로 성분이 양수이고 세로 성분이 음수인 화살표는 우측 아래를 가리키는 화살이 될 것이다.
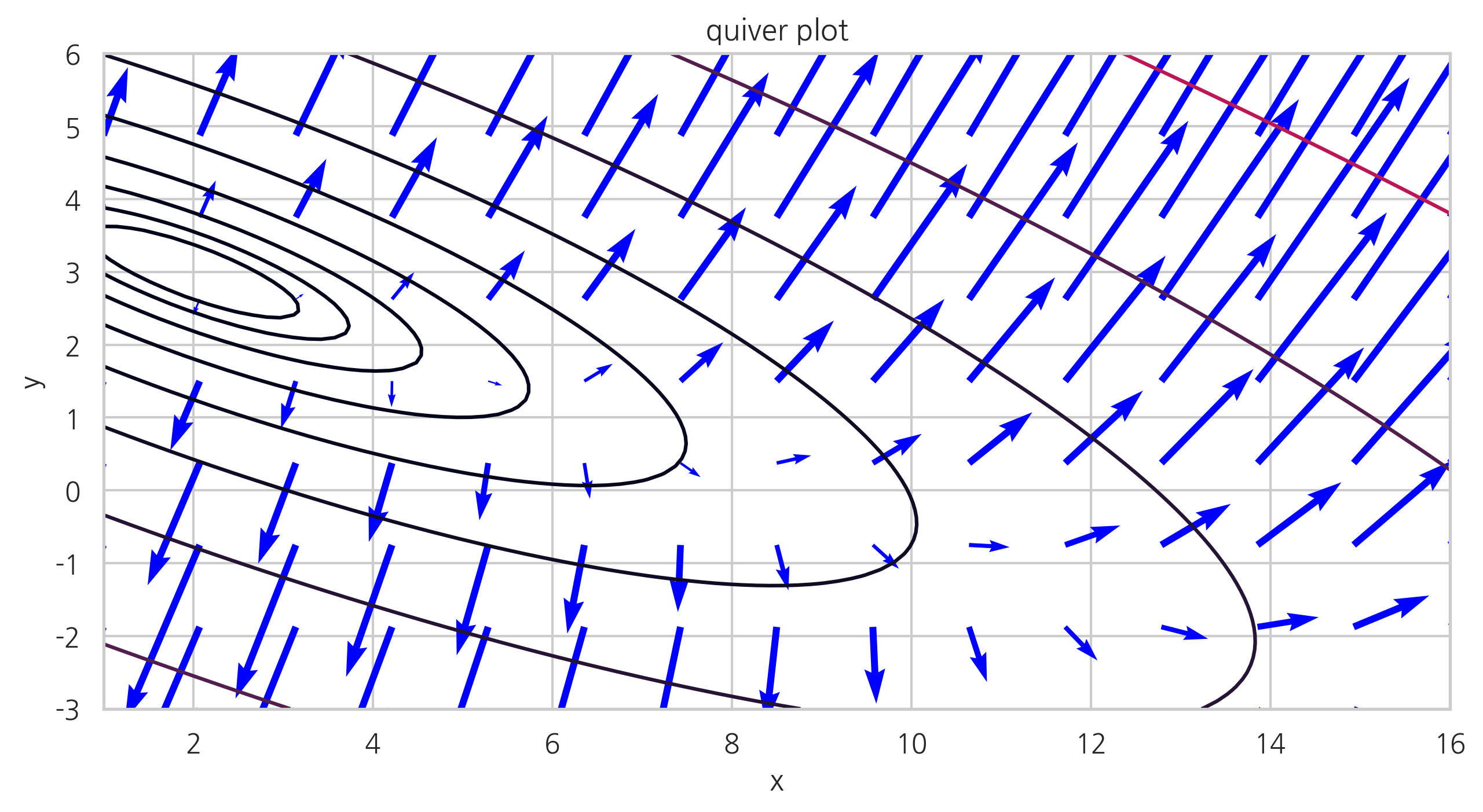
이렇게 컨투어 플롯 위에 그레디언트 벡터를 화살표로 나타낸 것을 플롯을 퀴버(quiver)플롯이라고 한다. 퀴버플롯에서 화살표는 화살표 시작 지점의 그레디언트 벡터를 나타낸다.
예제
다음은 함수
\[
\begin{align}
2x^2 + 6xy + 7y^2 - 26x - 54y + 107
\tag{4.4.19}
\end{align}
\]
의 그레디언트 벡터를 표시한 퀴버플롯이다.
연습 문제 4.4.3
함수
\[
\begin{align}
2x^2 + 6xy + 7y^2 - 26x - 54y + 107
\tag{4.4.20}
\end{align}
\]
로 표현되는 지형을 상상하라. 이 지형의 (14, 4) 지점에 공을 두었다면 어떠한 경로로 공이 움직일지 경로를 그려라.
퀴버플롯에서 그레디언트 벡터는 다음과 같은 특징이 있다.
그레디언트 벡터의 크기는 기울기를 의미한다. 즉 벡터의 크기가 클수록 함수 곡면의 기울기가 커진다.
그레디언트 벡터의 방향은 함수 곡면의 기울기가 가장 큰 방향, 즉 단위 길이당 함수값(높이)이 가장 크게 증가하는 방향을 가리킨다.
그레디언트 벡터의 방향은 등고선(isoline)의 방향과 직교한다.
어떤 점 \(x_0\)에서 다른 점 \(x\)로 이동하면서 함수 값이 얼마나 변하는지는 테일러 전개를 써서 근사할 수 있다.
\[
\begin{align}
f(x) - f(x_0) = \Delta f \approx \nabla f(x_0)^T (x - x_0)
\tag{4.4.21}
\end{align}
\]
변화의 방향 \(x - x_0\)가 그레디언트 벡터와 같은 방향일 때 \(\Delta f\)가 가장 커지는 것을 알 수 있다.
등고선은 \(f(x)\)의 값이 일정한 \(x\)의 집합이므로 다음과 같은 방정식으로 표현할 수 있다.
\[
\begin{align}
f(x) = f(x_0)
\tag{4.4.22}
\end{align}
\]
또는
\[
\begin{align}
f(x) - f(x_0) = 0
\tag{4.4.23}
\end{align}
\]
같은 등고선 위의 다른 점 \(x_1\)를 향해 움직이는 등고선 방향의 움직임은 \(x_1 - x_0\)이고 \(x_0\), \(x_1\) 모두 같은 등고선 위의 점이므로 \(f(x_0) = f(x_1)\)이다. 따라서 테일러 전개로부터
\[
\begin{align}
\nabla f(x_0)^T (x_1 - x_0) = f(x_1) - f(x_0) = 0
\tag{4.4.24}
\end{align}
\]
등고선 방향 \(x_1 - x_0\)과 \(\nabla f(x_0)\)이 직교한다는 것을 알 수 있다.
행렬미분법칙
다변수 함수를 미분하여 그레디언트 벡터를 구할 때는 다음 두가지 법칙이 유용하게 쓰인다.
행렬미분법칙 1: 선형 모형
선형 모형을 미분하면 그레디언트 벡터는 가중치 벡터이다.
\[
\begin{align}
f(x) = w^T x
\tag{4.4.25}
\end{align}
\]
\[
\begin{align}
\nabla f = \frac{\partial {w}^{T}{x}}{\partial {x}} = \frac{\partial {x}^{T}{w}}{\partial {x}} = {w}
\tag{4.4.26}
\end{align}
\]
(증명)
\[\begin{split}
\begin{align}
\dfrac{\partial ({w}^T {x})}{\partial {x}}=
\begin{bmatrix}
\boxed{\dfrac{\partial ({w}^T {x})}{\partial x_1}} \\
\boxed{\dfrac{\partial ({w}^T {x})}{\partial x_2}} \\
\vdots \\
\boxed{\dfrac{\partial ({w}^T {x})}{\partial x_N}} \\
\end{bmatrix} =
\begin{bmatrix}
\boxed{\dfrac{\partial (w_1 x_1 + \cancel{w_2 x_2} + \cdots + \cancel{w_N x_N})}{\partial x_1} \mathstrut} \\
\boxed{\dfrac{\partial (\cancel{w_1 x_1} + w_2 x_2 + \cdots + \cancel{w_N x_N})}{\partial x_2} \mathstrut} \\
\vdots \\
\boxed{\dfrac{\partial (\cancel{w_1 x_1} + \cancel{w_2 x_2} + \cdots + w_N x_N)}{\partial x_N} \mathstrut} \\
\end{bmatrix} =
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_N \\
\end{bmatrix}
= {w}
\tag{4.4.27}
\end{align}
\end{split}\]
행렬미분법칙 2: 이차 형식
이차 형식을 미분하면 행렬과 벡터의 곱으로 나타난다.
\[
\begin{align}
f(x) = x^T A x
\tag{4.4.28}
\end{align}
\]
\[
\begin{align}
\nabla f(x) = \frac{\partial {x}^{T}{A}{x}}{\partial {x}} = ({A} + {A}^{T}){x}
\tag{4.4.29}
\end{align}
\]
(증명)
\[\begin{split}
\begin{align}
\begin{aligned}
\dfrac{\partial ({x}^{T}{A}{x})}{\partial {x}}
&=
\begin{bmatrix}
\boxed{\dfrac{\partial ({x}^{T}{A}{x})}{\partial x_1}\mathstrut} \\
\boxed{\dfrac{\partial ({x}^{T}{A}{x})}{\partial x_2}\mathstrut} \\
\vdots \\
\boxed{\dfrac{\partial ({x}^{T}{A}{x})}{\partial x_N}\mathstrut} \\
\end{bmatrix} \\
&=
\begin{bmatrix}
\boxed{\dfrac{\partial (\sum_{i=1}^{N} \sum_{j=1}^{N} a_{ij} x_i x_j)}{\partial x_1}\mathstrut} \\
\boxed{\dfrac{\partial (\sum_{i=1}^{N} \sum_{j=1}^{N} a_{ij} x_i x_j)}{\partial x_2}\mathstrut} \\
\vdots \\
\boxed{\dfrac{\partial (\sum_{i=1}^{N} \sum_{j=1}^{N} a_{ij} x_i x_j)}{\partial x_N}\mathstrut} \\
\end{bmatrix} \\
&=
\begin{bmatrix}
\boxed{\dfrac{\partial
\left(
\begin{matrix}
a_{11}x_1x_1 &+& a_{12}x_1x_2 &+& \cdots &+& a_{1N}x_1x_N &+ \\
a_{21}x_2x_1 &+& \cancel{a_{22}x_2x_2} &+& \cdots &+& \cancel{a_{2N}x_2x_N} &+ \\
& & \cdots \\
a_{N1}x_Nx_1 &+& \cancel{a_{N2}x_Nx_2} &+& \cdots &+& \cancel{a_{NN}x_Nx_N} &
\end{matrix}
\right)}{\partial x_1} \mathstrut} \\
\boxed{\dfrac{\partial
\left(
\begin{matrix}
\cancel{a_{11}x_1x_1} &+& a_{12}x_1x_2 &+& \cdots &+& \cancel{a_{1N}x_1x_N} &+ \\
a_{21}x_2x_1 &+& a_{22}x_2x_2 &+& \cdots &+& a_{2N}x_2x_N &+ \\
& & \cdots \\
\cancel{a_{N1}x_Nx_1} &+& a_{N2}x_Nx_2 &+& \cdots &+& \cancel{a_{NN}x_Nx_N} &
\end{matrix}
\right)}{\partial x_2}\mathstrut} \\
\vdots \\
\end{bmatrix}
\\
&=
\begin{bmatrix}
\boxed{\begin{matrix}
2a_{11}x_1 &+& a_{12}x_2 &+& \cdots &+& a_{1N}x_N &+& \\
a_{21}x_2 &+& 0 &+& \cdots &+& 0 &+& \\
& & & \cdots & & & & \\
a_{N1}x_N &+& 0 &+& \cdots &+& 0 & &
\end{matrix} \mathstrut} \\
\boxed{\begin{matrix}
0 &+& a_{12}x_2 &+& \cdots &+& 0 &+& \\
a_{21}x_1 &+& 2a_{22}x_2 &+& \cdots &+& a_{2N}x_N &+& \\
& & \cdots & & & & & & \\
0 &+& a_{N2}x_N &+& \cdots &+& 0 & &
\end{matrix} \mathstrut} \\
\vdots \\
\end{bmatrix} \\
&=
\begin{bmatrix}
\boxed{\sum_{i=1}^{N} a_{1i} x_i + \sum_{i=1}^{N} a_{i1} x_i} \\
\boxed{\sum_{i=1}^{N} a_{2i} x_i + \sum_{i=1}^{N} a_{i2} x_i} \\
\vdots \\
\boxed{\sum_{i=1}^{N} a_{Ni} x_i + \sum_{i=1}^{N} a_{iN} x_i} \\
\end{bmatrix} \\ \\
&=
\begin{bmatrix}
\boxed{\sum_{i=1}^{N} a_{1i} x_i} \\
\boxed{\sum_{i=1}^{N} a_{2i} x_i} \\
\vdots \\
\boxed{\sum_{i=1}^{N} a_{Ni} x_i} \\
\end{bmatrix}
+
\begin{bmatrix}
\boxed{\sum_{i=1}^{N} a_{i1} x_i} \\
\boxed{\sum_{i=1}^{N} a_{i2} x_i} \\
\vdots \\
\boxed{\sum_{i=1}^{N} a_{iN} x_i} \\
\end{bmatrix} \\ \\
&=
{A} {x} + {A}^T {x}
=
({A} + {A}^T){x}
\end{aligned}
\tag{4.4.30}
\end{align}
\end{split}\]
위의 두 가지 경우는 1차 다항식과 2차 다항식에 대한 스칼라 미분과 비슷하다. 두 경우를 비교해 보면 이 공식을 외우는데 도움이 된다.
벡터를 스칼라로 미분하는 경우
벡터
\[\begin{split}
\begin{align}
{f}(x) =
\begin{bmatrix}
f_1 \\
f_2 \\
\vdots\\
f_M \\
\end{bmatrix}
\tag{4.4.35}
\end{align}
\end{split}\]
를 스칼라 \(x\)로 미분하는 경우에는 결과를 행 벡터로 표시한다.
\[
\begin{align}
\frac{\partial {f}}{\partial x} =
\begin{bmatrix}
\dfrac{\partial f_1}{\partial x} &
\dfrac{\partial f_2}{\partial x} &
\cdots &
\dfrac{\partial f_M}{\partial x}
\end{bmatrix}
\tag{4.4.36}
\end{align}
\]
벡터를 벡터로 미분하는 경우
벡터 \({x}\)를 입력받아 벡터를 출력하는 함수 \(f(x)\)를 생각하자.
벡터를 벡터로 미분하면 미분을 당하는 벡터의 원소가 여러개(\(i=1, \dots, N\))이고 미분을 하는 벡터의 원소도 여러개(\(j=1, \dots, M\))이므로 미분의 결과로 나온 도함수는 2차원 배열 즉, 행렬이 된다.
\[\begin{split}
\begin{align}
\dfrac{\partial {f}}{\partial {x}}
=
\begin{bmatrix}
\dfrac{\partial f_1}{\partial {x}} &
\dfrac{\partial f_2}{\partial {x}} &
\cdots &
\dfrac{\partial f_N}{\partial {x}}
\end{bmatrix}
=
\begin{bmatrix}
\dfrac{\partial {f}}{\partial x_1} \\
\dfrac{\partial {f}}{\partial x_2} \\
\vdots \\
\dfrac{\partial {f}}{\partial x_M}
\end{bmatrix}
=
\begin{bmatrix}
\dfrac{\partial f_1}{\partial x_1} & \dfrac{\partial f_2}{\partial x_1} & \cdots & \dfrac{\partial f_N}{\partial x_1} \\
\dfrac{\partial f_1}{\partial x_2} & \dfrac{\partial f_2}{\partial x_2} & \cdots & \dfrac{\partial f_N}{\partial x_2} \\
\vdots & \vdots & \ddots & \vdots \\
\dfrac{\partial f_1}{\partial x_M} & \dfrac{\partial f_2}{\partial x_M} & \cdots & \dfrac{\partial f_N}{\partial x_M} \\
\end{bmatrix}
\tag{4.4.37}
\end{align}
\end{split}\]
행렬미분법칙 3: 행렬과 벡터의 곱의 미분
행렬 \(A\)와 벡터 \(x\)의 곱 \(Ax\)를 벡터 \(x\)로 미분하면 행렬 \(A^T\)가 된다.
\[
\begin{align}
f(x) = Ax
\tag{4.4.38}
\end{align}
\]
\[
\begin{align}
\nabla f(x) = \dfrac{\partial ({Ax})}{\partial {x}} = A^T
\tag{4.4.39}
\end{align}
\]
(증명)
\[
\begin{align}
{Ax} = {c_1}x_1 + {c_2}x_2 + \cdots + {c_M}x_M
\tag{4.4.40}
\end{align}
\]
\[\begin{split}
\begin{align}
\dfrac{\partial ({Ax})}{\partial {x}}
=
\begin{bmatrix}
\dfrac{\partial ({Ax})}{\partial x_1} \\
\dfrac{\partial ({Ax})}{\partial x_2} \\
\cdots \\
\dfrac{\partial ({Ax})}{\partial x_M}
\end{bmatrix}
=
\begin{bmatrix}
\dfrac{\partial ({c_1}x_1 + {c_2}x_2 + \cdots + {c_M}x_M)^T}{\partial x_1} \\
\dfrac{\partial ({c_1}x_1 + {c_2}x_2 + \cdots + {c_M}x_M)^T}{\partial x_2} \\
\cdots \\
\dfrac{\partial ({c_1}x_1 + {c_2}x_2 + \cdots + {c_M}x_M)^T}{\partial x_M}
\end{bmatrix}
=
\begin{bmatrix}
{c_1}^T \\
{c_2}^T \\
\cdots \\
{c_M}^T
\end{bmatrix}
= A^T
\tag{4.4.41}
\end{align}
\end{split}\]
함수의 출력변수와 입력변수가 모두 벡터(다차원) 데이터인 경우에는 입력변수 각각과 출력변수 각각의 조합에 대해 모두 미분이 존재한다. 따라서 도함수는 행렬 형태가 된다. 이렇게 만들어진 도함수의 행렬을 자코비안 행렬(Jacobian matrix) 이라고 한다. 자코비안 행렬은 벡터함수를 벡터변수로 미분해서 생기는 행렬의 전치행렬이다. 따라서 행/열의 방향이 다르다는 점에 유의한다.
\[\begin{split}
\begin{align}
Jf(x) = J = \left(\frac{\partial f}{\partial x}\right)^T =
\begin{bmatrix}
\left(\dfrac{\partial f_1}{\partial x}\right)^T \\ \vdots \\ \left(\dfrac{\partial f_M}{\partial x}\right)^T
\end{bmatrix} =
\begin{bmatrix}
\nabla f_1^T \\ \vdots \\ \nabla f_M^T \\
\end{bmatrix} =
\begin{bmatrix}
\dfrac{\partial f_1}{\partial x_1} & \cdots & \dfrac{\partial f_1}{\partial x_N}\\
\vdots & \ddots & \vdots\\
\dfrac{\partial f_M}{\partial x_1} & \cdots & \dfrac{\partial f_M}{\partial x_N}
\end{bmatrix}
\tag{4.4.42}
\end{align}
\end{split}\]
연습 문제 4.4.4
다음 함수의 자코비안 행렬을 구하라
\[\begin{split}
\begin{align}
f(x) =
\begin{bmatrix}
\displaystyle\sum_{i=1}^3 x_i \\
\displaystyle\prod_{i=1}^3 x_i
\end{bmatrix}
\tag{4.4.43}
\end{align}
\end{split}\]
다변수 함수의 2차 도함수는 그레디언트 벡터를 입력변수 벡터로 미분한 것으로 **헤시안 행렬(Hessian matrix)**이라고 한다.
헤시안 행렬은 그레디언트 벡터의 자코비안 행렬의 전치 행렬로 정의한다.
\[
\begin{align}
Hf(x) = H = J(\nabla f(x))^T
\tag{4.4.44}
\end{align}
\]
풀어쓰면 다음과 같다.
\[
\begin{align}
H_{ij} = \dfrac{\partial^2 f}{\partial x_i\,\partial x_j}
\tag{4.4.45}
\end{align}
\]
즉,
\[\begin{split}
\begin{align}
H = \begin{bmatrix}
\dfrac{\partial^2 f}{\partial x_1^2} & \dfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \dfrac{\partial^2 f}{\partial x_1\,\partial x_N} \\
\dfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \dfrac{\partial^2 f}{\partial x_2^2} & \cdots & \dfrac{\partial^2 f}{\partial x_2\,\partial x_N} \\
\vdots & \vdots & \ddots & \vdots \\
\dfrac{\partial^2 f}{\partial x_N\,\partial x_1} & \dfrac{\partial^2 f}{\partial x_N\,\partial x_2} & \cdots & \dfrac{\partial^2 f}{\partial x_N^2}
\end{bmatrix}
\tag{4.4.46}
\end{align}
\end{split}\]
함수가 연속이고 미분가능한 함수라면 헤시안 행렬은 대칭행렬이 된다.
연습 문제 4.4.5
다음 함수의 헤시안 행렬을 구하라
\[
\begin{align}
f(x) = \sum_{i=1}^3 x_i^2
\tag{4.4.47}
\end{align}
\]
스칼라를 행렬로 미분
출력변수 \(f\)가 스칼라값이고 입력변수 \(X\)가 행렬인 경우에는 도함수 행렬의 모양이 입력변수 행렬 \(X\)와 같다.
\[\begin{split}
\begin{align}
\dfrac{\partial f}{\partial {X}} =
\begin{bmatrix}
\dfrac{\partial f}{\partial x_{1,1}} & \dfrac{\partial f}{\partial x_{1,2}} & \cdots & \dfrac{\partial f}{\partial x_{1,N}}\\
\dfrac{\partial f}{\partial x_{2,1}} & \dfrac{\partial f}{\partial x_{2,2}} & \cdots & \dfrac{\partial f}{\partial x_{2,N}}\\
\vdots & \vdots & \ddots & \vdots\\
\dfrac{\partial f}{\partial x_{M,1}} & \dfrac{\partial f}{\partial x_{M,2}} & \cdots & \dfrac{\partial f}{\partial x_{M,N}}\\
\end{bmatrix}
\tag{4.4.48}
\end{align}
\end{split}\]
행렬미분법칙 4: 행렬 곱의 대각성분
두 정방행렬을 곱해서 만들어진 행렬의 대각성분(trace)는 스칼라이다. 이 스칼라를 뒤의 행렬로 미분하면 앞의 행렬의 전치행렬이 나온다.
\[
\begin{align}
f(X) = \text{tr} ({W}{X})
\tag{4.4.49}
\end{align}
\]
\[
\begin{align}
{W} \in {R}^{N \times N}, {X} \in {R}^{N \times N}
\tag{4.4.50}
\end{align}
\]
\[
\begin{align}
\dfrac{\partial f}{\partial X} =
\dfrac{\partial \, \text{tr} ({W}{X})}{\partial {X}} = {W}^T
\tag{4.4.51}
\end{align}
\]
(증명)
\[
\begin{align}
\text{tr}({W}{X}) = \sum_{i=1}^N \sum_{j=1}^N w_{ji} x_{ij}
\tag{4.4.52}
\end{align}
\]
\[
\begin{align}
\dfrac{\partial \text{tr} ({W}{X})}{\partial x_{ij}} = w_{ji}
\tag{4.4.53}
\end{align}
\]
행렬미분법칙 5: 행렬식의 로그
행렬식(determinant)은 스칼라값이고 이 값의 로그 값도 스칼라이다. 이 값을 원래의 행렬로 미분하면 원래 행렬의 역행렬의 전치 행렬이 된다.
\[
\begin{align}
f(X) = \log | {X} |
\tag{4.4.54}
\end{align}
\]
\[
\begin{align}
\dfrac{\partial f}{\partial X} = \dfrac{\partial \log | {X} | }{\partial {X}} = ({X}^{-1})^T
\tag{4.4.55}
\end{align}
\]
(증명)
행렬식의 정의에서
\[
\begin{align}
\dfrac{\partial}{\partial x_{i,j}} \vert X \vert = C_{i,j}
\tag{4.4.56}
\end{align}
\]
행렬식과 역행렬의 관계에서
\[
\begin{align}
\dfrac{\partial}{\partial X} \vert X \vert = C = | X | (X^{-1})^T
\tag{4.4.57}
\end{align}
\]
로그 함수 공식에 대입하면
\[
\begin{align}
\dfrac{d}{dx} \log f(x) = \dfrac{f'(x)}{f(x)} = \dfrac{\vert X \vert (X^{-1})^T}{\vert X \vert} = (X^{-1})^T
\tag{4.4.58}
\end{align}
\]