1.1 데이터 분석의 소개#
데이터 분석이란#
데이터 분석이란 어떤 데이터가 주어졌을 때,
데이터 간의 관계를 파악하거나
파악된 관계를 사용하여 우리가 원하는 새로운 (출력) 데이터를 만들어 내는 과정
으로 볼 수 있다.
데이터 분석도 분석 목적에 따라 “예측(prediction)”, “클러스터링(clustering)”, “모사(approximation)” 등 다양한 문제가 있다. 여기에서는 가장 널리 사용되는 예측 문제를 살펴본다.
예측#
**예측(prediction)**은 데이터 분석 작업 중 가장 많이 사용되는 유형 중 하나이다. 예측이란 숫자, 문서, 이미지, 음성, 영상 등의 여러 가지 입력 데이터를 주면, 데이터 분석의 결과로 다른 데이터를 출력하는 분석 방법이다.

그림 1.1.1 : 예측 모형
예를 들어 다음과 같은 작업은 예측이라고 할 수 있다.
부동산의 위치, 주거환경, 건축연도 등을 주면 해당 부동산의 가치를 추정한다.
꽃잎의 길이와 너비 등 식물의 외형적 특징을 주면 해당하는 식물의 종을 알아낸다.
얼굴 사진을 주면 해당하는 사람의 이름을 출력한다.
현재 바둑돌의 위치들을 주면 다음 바둑돌의 위치를 지정한다.
데이터 분석에서 말하는 예측이라는 용어는 시간상으로 미래의 의미는 포함하지 않는다. 시계열 분석에서는 시간상으로 미래의 데이터를 예측하는 경우가 있는데 이 때는 미래예측(forecasting) 이라는 용어를 사용한다.
연습 문제 1.1.1#
예측 문제로 풀 수 있는 데이터 분석의 예를 3가지 생각해 보자.
입력 데이터와 출력 데이터#
예측 문제에서는 데이터의 유형을 **입력 데이터(input data)**와 **출력 데이터(output data)**라는 두 가지 유형의 데이터로 분류할 수 있어야 한다.
입력 데이터는 분석의 기반이 되는 데이터로 보통 알파벳 \(X\)로 표기한다. 다른 말로 독립변수(independent variable), 특징(feature), 설명변수(explanatory variable) 등의 용어를 쓰기도 한다.
출력 데이터는 추정하거나 예측하고자 하는 목적 데이터를 말한다. 보통 알파벳 \(Y\)로 표기하며, 다른 말로 종속변수(dependent variable)라고 부른다. 종속변수가 뒤에서 설명할 카테고리값이면 라벨(label) 또는 클래스(class)라고 하기도 한다.
입력 데이터와 출력 데이터를 정확히 파악하는 것은 예측 문제를 구체화하는 첫 번째 단계이다. 특히 예측 성능은 이러한 입출력 데이터의 숫자와 종류에 크게 의존하기 때문에 정확히 어떠한 값을 가지는 입력을 몇 개 사용하겠다는 문제 정의가 예측 문제를 해결하는 데 가장 중요한 부분이 될 수도 있다.
연습 문제 1.1.2#
연습 문제 1.1.1에서 생각한 3가지 예측 문제의 입력과 출력을 보다 정확하게 정의해 보자. 중요한 점은 다음과 같다.
“~등”, “같은 것”이란 용어를 사용하지 않고 정확히 입출력 데이터의 개수를 정해야 한다.
입력이나 출력 데이터값의 숫자 예를 제시하면 더욱 좋다. 예를 들어, 부동산 가격을 예측하기 위해 면적을 입력 데이터로 사용하기로 했다면, “40 제곱미터” 혹은 “80 제곱미터”와 같이 실제로 어떤 숫자를 입력데이터로 사용할지 예를 든다.
규칙기반 방법과 학습기반 방법#
그럼 이런 예측 문제를 풀려면 어떤 방법을 써야 할까? 예측을 하기 위한 방법론으로는 규칙기반(rule-based) 방법과 학습기반(traing-based) 또는 데이터기반(data-based) 방법이라는 두 가지 방법이 사용된다.
규칙기반 방법은 어떤 입력이 들어오면 어떤 출력이 나오는지를 결정하는 규칙이나 알고리즘을 사람이 미리 만들어 놓는 방법이다. 학습기반 방법 또는 데이터기반 방법은 이러한 규칙을 사람이 만드는 것이 아니라, 대량의 데이터를 컴퓨터에 보여줌으로써 스스로 규칙을 만들게 하는 방법이다. 여기에서는 규칙기반 방법은 다루지 않으며 학습기반 방법만을 다루도록 한다.
예를 들어 개를 찍은 사진을 입력하면 “개”라고 출력하고, 고양이를 찍은 사진을 입력하면 “고양이”라고 출력하는 예측 시스템을 만든다고 가정해 보자.
규칙기반 방법을 사용하면 사진에서 눈 모양을 찾아내는 알고리즘을 넣고 눈동자가 세로 방향으로 길면 고양이이고, 아니면 개라고 출력하는 규칙을 넣을 수 있다. 이렇게 사람이 세부적인 규칙을 알려주는 방법이 규칙기반 방법이다. 또한 번역의 예를 들면, 특정한 영어 단어가 어떤 의미로 번역되는지를 어떤 품사를 가지는지를 알려주는 사전(dictionary)도 규칙 집합으로 볼 수 있고, 이러한 규칙을 조합하여 영어 문장을 한국어 문장으로 번역할 수 있다.
이와 대조적으로 학습기반 방법은 이러한 규칙을 알려주지 않는 대신 많은 데이터를 주고 스스로 규칙을 찾도록 한다. 앞서 말한 고양이와 개의 구분 문제에서는 개와 고양이를 찍은 사진을 주고 스스로 적합한 규칙을 찾도록 하며, 영어를 한국어로 번역하는 문제에서는 수많은 영어 문장과 이에 대응하는 한국어 문장을 주고 스스로 번역 방법을 찾도록 한다.
연습 문제 1.1.3#
연습 문제 1.1.1과 1.1.2에서 생각한 3가지 예측 문제에 대해 규칙기반의 해결 방법을 생각해보자. 정확한 답이 아니어도 괜찮다.
지도학습#
학습기반 예측 방법론을 사용하려면 학습용 데이터 집합(training data set)을 사람이 만들어 주어야 한다. 학습용 데이터 집합은 입력값과 목푯값(정답)을 쌍으로 가지는 표본 데이터의 집합이다. 이는 학습시키고자 하는 예측 시스템이 최종적으로 동작하기를 바라는 모습을 표현한 데이터 집합이라고 볼 수 있다.
예를 들어 개를 찍은 사진을 입력하면 “개”라고 출력하고, 고양이를 찍은 사진을 입력하면 “고양이”라고 출력하는 예측 시스템을 만들고 싶다면 개를 찍은 사진과 고양이를 찍은 사진을 준비해서 다음과 같이 학습용 데이터 집합을 만들어야 한다.

그림 1.1.2 학습용 데이터 예
각각의 사진에 “개” 혹은 “고양이”라는 출력 데이터(목표)값을 붙이는 작업은 당연히 사람이 수동으로 해야 한다. 그래서 이러한 방법을 지도학습(supervised learning) 방법이라고 한다.
비유를 들자면 학습용 데이터 집합이란 정답이 표시된 수백 개의 문제를 모아놓은 문제집과 같고, 지도학습이란 이 문제집을 컴퓨터에 주고 학습시키는 것과 같다. 컴퓨터는 이 수백 개의 문제를 나름의 풀이방법으로 스스로 풀어본 다음, 정답을 이용하여 얼마나 맞았는지를 채점한다. 그런 다음 풀이방법을 스스로 조금씩 바꾸어 보면서 풀이와 채점을 반복한다. 이 과정을 반복하는 것이 지도학습이다. 따라서 지도학습이 얼마나 잘 되는가는 학습용 데이터의 양과 질에 크게 의존한다.
학습용 데이터 집합에 붙어있는 출력 데이터, 즉 정답을 **목푯값(target)**이라고 한다. 지도학습의 목표는 주어진 목푯값과 최대한 비슷한 값을 출력하는 예측 방법을 찾아내는 것이다. 만약 입력데이터만 있고 이에 대응하는 목푯값이 없다면 각 입력데이터에 대해 사람이 원하는 목표값을 붙어 주어야 한다. 이러한 작업을 **레이블링(labelling)**이라고 한다. 데이터의 양이 많고 복잡한 시스템을 만드는 경우에는 목푯값을 만드는 일, 즉 학습데이터를 만드는 일이 현실적으로 상당히 어려운 일이 될 수도 있다.

그림 1.1.3 : 지도학습의 원리
이미지넷#
이미지넷(ImageNet)은 페이페이 리(Fei-Fei Li) 교수가 이끄는 인공지능 팀이 만들어 2009년에 공개한 학습용 데이터셋이다. 320만장 이상의 이미지를 5,247개의 카테고리로 분류하였다. 이 작업은 아마존 미케니컬 터크(Amazon Mechanical Turk)라는 서비스를 통해 레이블링하였는데 이 서비스는 인터넷을 통해 전 세계에의 원하는 사람에게 간단한 작업을 지시하고 보수를 주는 시스템이다. 즉 인터넷을 통해 전 세계의 저비용 노동력을 사용하긴 했지만 결국 사람이 하나하나 이미지를 보면서 올바른 카테고리를 붙이는 작업을 한 것이다.
이미지넷 시스템을 공개한 후 이를 기반으로 ILSVRC(ImageNet Large Scale Visual Recognition Challenge)라는 이미지 인식 경연대회가 열렸다. 2010년에 열린 첫번째 대회의 목표는 1000개의 카테고리를 가지는 120만장의 이미지를 학습데이터로 사용하고 20만장의 테스트 데이터를 이용하여 학습성능을 확인하는 것이었다. 이 대회를 통해 AlexNet 등의 딥러닝 시스템의 우수성이 알려지기 시작하여 새로운 머신러닝의 시대가 열리게 되었다.
보다 자세한 내용은 온라인 미디어 쿼츠(Quartz)의 기사를 참조하라( https://qz.com/1034972/the-data-that-changed-the-direction-of-ai-research-and-possibly-the-world/ ).
연습 문제 1.1.4#
지금까지 생각한 3가지 예측 문제에 대해 학습용 데이터 집합을 만들어본다. 학습용 데이터 집합의 크기는 최소한 각 문제에 대해 10개 이상 만들어보자.
연습 문제 1.1.5#
어떤 데이터 사이언티스트가 많은 문서를 자동으로 몇가지 카테고리로 분류할 수 있는 기능을 만들고 싶어한다. 즉 문서를 입력 데이터로 넣으면 해당하는 카테고리가 출력 데이터로 나오기를 원한다. 그녀는 이러한 기능을 지도학습을 이용하여 만들기로 결정했는데 지도학습을 사용하려면 이미 출력 데이터가 붙어 있는, 즉 이미 분류가 되어 있는 학습데이터가 있어야 한다는 것을 알게 되었다. 이러한 레이블링 작업이 어렵기 때문에 한가지 꼼수를 생각해 내었는데 그 방법은 다음과 같다. 우선 문서에 포함된 단어 등을 보고 문서의 카테고리를 유추하는 간단한 규칙기반 시스템을 만든다. 이를 사용하여 입력데이터의 목푯값을 자동으로 레이블링하고 이 데이터를 학습데이터로 사용하여 지도학습을 하는 방법이다.
이 접근법의 문제점은 무엇인가? 만약 지도학습이 성공한다면 그 시스템의 성능은 레이블링을 위해 만든 규칙기반 시스템과 어떻게 다른가?
전처리와 인코딩#
앞에서 숫자, 문서, 이미지, 음성, 영상 등의 여러 가지 데이터를 처리하는 것을 예시로 들었지만, 안타깝게도 현재 기술상 컴퓨터가 직접 처리할 수 있는 데이터는 사실 숫자(number)밖에 없다. 그렇다면 문서나 이미지와 같은 데이터는 어떻게 처리하는 것일까? 데이터 분석에서는 전처리(preprocessing) 또는 **인코딩(encoding)**이라는 과정을 통해 문서나 이미지와 같은 현실의 데이터를 컴퓨터가 처리할 수 있는 숫자 데이터로 바꾸어야 한다. 따라서 실제 예측 모형은 사실 다음과 같은 형태가 된다.

그림 1.1.4 : 전처리/인코딩이 포함된 예측 모형
전처리는 단순히 비정형 데이터를 숫자로 바꾸는 것만 의미하는 것이 아니다. 전체 입력 정보 중 실제로 출력 데이터의 결정에 영향을 미칠만한 핵심 정보를 선택하거나 복수의 입력 데이터를 조합하여 새로운 입력 데이터를 만드는 것도 전처리의 중요한 역할이다. 전처리 과정은 최종 예측 성능에 커다란 영향을 끼친다.
연습 문제 1.1.6#
지금까지 생각한 예측 문제의 입력 데이터 중 전처리 혹은 인코딩이 필요한 것이 어떤 것인지 확인하고 어떻게 숫자로 바꿀 수 있을지 그 방법을 생각해 보자.
인코딩의 예: 이미지 데이터#
실제로 이미지 데이터는 어떻게 숫자로 바뀌는지를 살펴보자. 다음 데이터는 “MNIST handwritten digit image”라는 표본 데이터 중 하나이다. 이 데이터는 손글씨를 영상으로 나타낸 것으로 다음 그림은 숫자 0을 손으로 쓴 후 카메라로 찍어 8x8의 저해상도 이미지로 저장한 것이다.
여기에 나오는 모든 코드는 https://hub.docker.com/r/datascienceschool/rpython/ 에서 제공하는 도커 컨테이너 상에서 바로 실행할 수 있다. 자세한 내용은 2 장에서 다루도록 한다.
MNIST handwritten digit 데이터중 첫번째 이미지 출력
from sklearn.datasets import load_digits
digits = load_digits()
sns.heatmap(digits.images[0], cmap=mpl.cm.bone_r, annot=True, fmt="2.0f",
cbar=True, xticklabels=False, yticklabels=False)
plt.title("MNIST 숫자 이미지 표본")
plt.show()
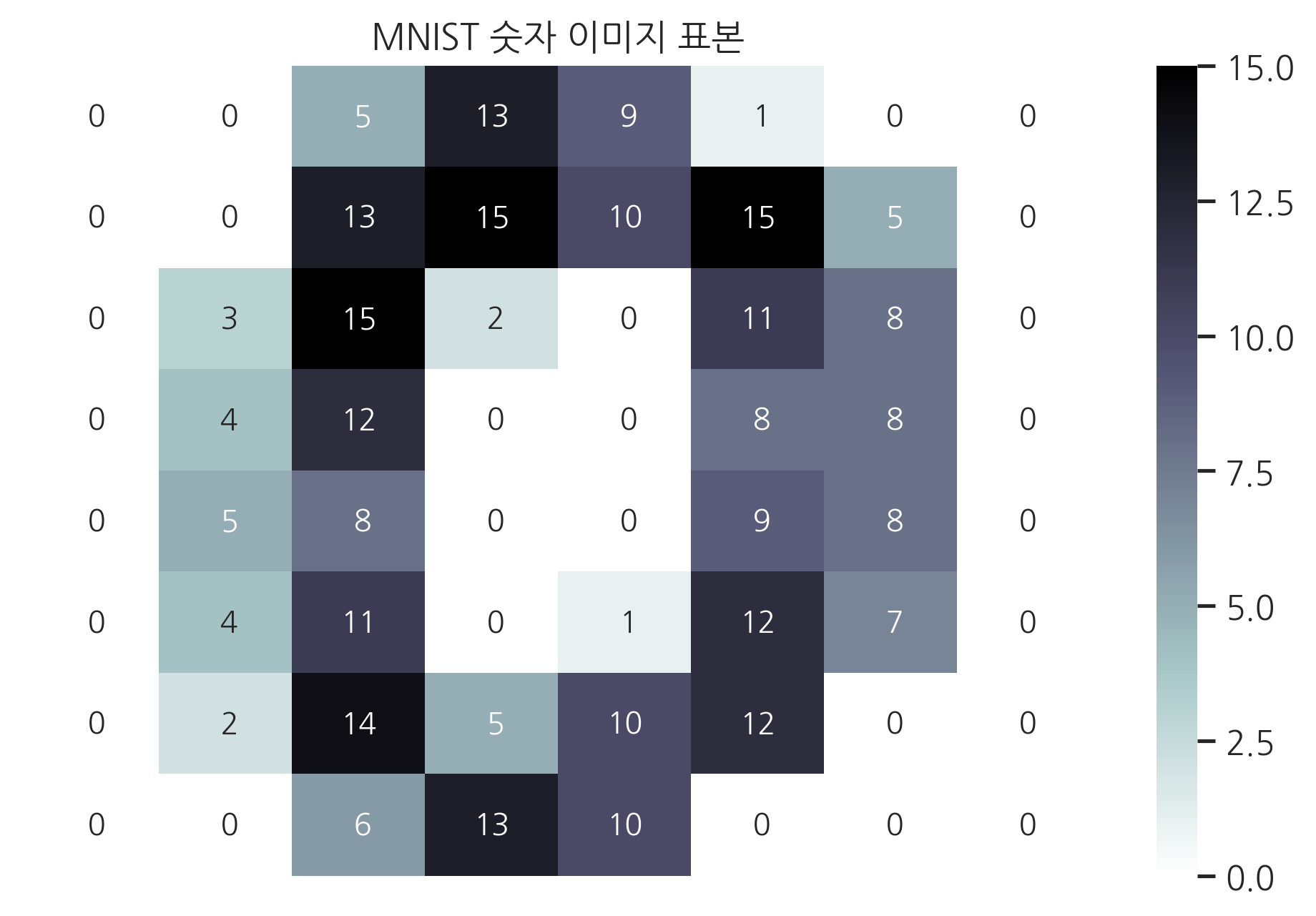
이 이미지는 다음과 같은 8x8 행렬에 명도를 나타내는 숫자로 저장된다. 0은 백색이고 15가 가장 진한 색을 뜻한다.
digits.images[0]
array([[ 0., 0., 5., 13., 9., 1., 0., 0.],
[ 0., 0., 13., 15., 10., 15., 5., 0.],
[ 0., 3., 15., 2., 0., 11., 8., 0.],
[ 0., 4., 12., 0., 0., 8., 8., 0.],
[ 0., 5., 8., 0., 0., 9., 8., 0.],
[ 0., 4., 11., 0., 1., 12., 7., 0.],
[ 0., 2., 14., 5., 10., 12., 0., 0.],
[ 0., 0., 6., 13., 10., 0., 0., 0.]])
그리고 이 이미지 데이터는 다음과 같은 64-길이의 숫자 벡터로 바뀌어 예측 모형에 입력된다.
digits.images[0].flatten()
array([ 0., 0., 5., 13., 9., 1., 0., 0., 0., 0., 13., 15., 10.,
15., 5., 0., 0., 3., 15., 2., 0., 11., 8., 0., 0., 4.,
12., 0., 0., 8., 8., 0., 0., 5., 8., 0., 0., 9., 8.,
0., 0., 4., 11., 0., 1., 12., 7., 0., 0., 2., 14., 5.,
10., 12., 0., 0., 0., 0., 6., 13., 10., 0., 0., 0.])

그림 1.1.5 : 이미지를 입력으로 가지는 예측 모형의 예
입력 차원#
앞에서 다룬 모형에서 중요한 점은 입력의 개수 즉, 숫자 벡터의 크기이다. 이를 **입력 차원(input dimension)**이라고 부르는데 일반적으로 입력 차원은 일단 정해지면 바꿀 수 없고 고정되어야 한다.
즉, 앞의 예제와 같이 64개의 숫자 입력을 가지는 경우, 다시 말해서 입력 차원이 64인 예측 시스템을 만들었다면 이 모형에는 128개의 숫자 입력은 적용할 수 없다. 따라서 해상도가 128차원인 이미지를 입력 데이터로 써서 예측하려면 여기에 맞는 128차원 입력 예측 모형을 처음부터 새로 만들든지, 아니면 128차원 데이터를 어떤 방법으로든 64차원으로 줄이는 방법밖에 없다.
인코딩의 다른 예 : 문서 데이터#
그럼 문서 데이터는 어떻게 인코딩하여 숫자로 변환할까? 문서 데이터를 숫자로 변환할 때 가장 어려운 점은 영상과 달리 크기가 제각각이라는 점이다. 즉, 5개 단어로 이루어진 한 문장으로 된 문서도 있고, 수천 개의 단어로 이루어진 장문의 문서도 있는데 이것을 같은 크기의 숫자로 바꾸어야 한다.
이러한 문서 데이터를 고정된 크기의 숫자 벡터로 바꾸는 방법 중 가장 널리 쓰이는 것은 **’BOW(Bag of Words)’**라는 방법이다. 이 방법은 문서를 이루는 단어의 순서, 의미 등의 정보를 모두 무시하고 오로지 특정한 단어가 문서에 몇 번 나왔는지만 세어 그 빈도를 벡터로 표시하는 방법이다.
예를 들어 대부분의 문서가 10,000개의 단어 중 일부로 구성되어 있다면, 각 단어에 1부터 10,000이라는 번호를 붙인다. 이를 단어장(vovaulary)이라고 한다. 그리고 어떤 하나의 문서를 하나의 숫자 벡터로 바꾸려면 해당 문서에 1번 단어가 한 번 나오면 숫자 벡터의 첫번째 원소값이 1이 되고, 2번 단어가 한 번도 나오지 않는다면 숫자 벡터의 두 번째 원소값이 0이 된다. 이러한 방식으로 어떤 길이를 가지는 문서든 10,000개의 길이를 가지는 숫자 벡터로 바꿀 수 있다.
다음 예제는 “20 newsgroups” 라고 불리는 문서 표본 데이터의 하나이다. 여기에서 첫번째 데이터(문서)는 다음과 같다.
20 newsgroups 데이터중 첫번째 문서 출력
from sklearn.datasets import fetch_20newsgroups
news = fetch_20newsgroups()
print("입력:\n", news.data[0])
print("출력:\n", news.target_names[news.target[0]])
입력:
From: lerxst@wam.umd.edu (where's my thing)
Subject: WHAT car is this!?
Nntp-Posting-Host: rac3.wam.umd.edu
Organization: University of Maryland, College Park
Lines: 15
I was wondering if anyone out there could enlighten me on this car I saw
the other day. It was a 2-door sports car, looked to be from the late 60s/
early 70s. It was called a Bricklin. The doors were really small. In addition,
the front bumper was separate from the rest of the body. This is
all I know. If anyone can tellme a model name, engine specs, years
of production, where this car is made, history, or whatever info you
have on this funky looking car, please e-mail.
Thanks,
- IL
---- brought to you by your neighborhood Lerxst ----
출력:
rec.autos
이 문서중 100개를 위에서 설명한 BOW 인코딩을 하면 6,288개의 단어장을 가지는 행렬로 바꿀 수 있다.
20 newsgroups 문서 데이터를 숫자 벡터로 변환
from sklearn.feature_extraction.text import CountVectorizer
vec = CountVectorizer(stop_words="english").fit(news.data[:100])
data = vec.transform(news.data[:100])
data.shape
(100, 6288)
사실 하나의 문서는 6288개의 단어 중 일부 단어만으로 이루어지므로 숫자 벡터의 대부분은 0이 된다. 앞에서 말한 이미지 인코딩 방법을 반대로 적용하여 이 행렬을 이미지로 바꾸면 다음과 같다. 여기에서는 전체 행렬 중 일부(50개의 문서와 100번째 단어까지)만을 이미지로 바꾸었다. 이 이미지에서 하나의 행(row)은 하나의 문서를 뜻하고, 까만 점으로 나타나는 부분이 특정한 단어가 그 문서안에 포함된 단어를 의미한다.
sns.heatmap(data.toarray()[:50, :100], cmap=mpl.cm.bone_r,
linewidths=0.001, linecolor='gray', cbar=False,
xticklabels=False, yticklabels=False)
plt.xlabel("단어")
plt.ylabel("문서")
plt.title("BOW(Bag of Words) 인코딩 결과 시각화")
plt.show()
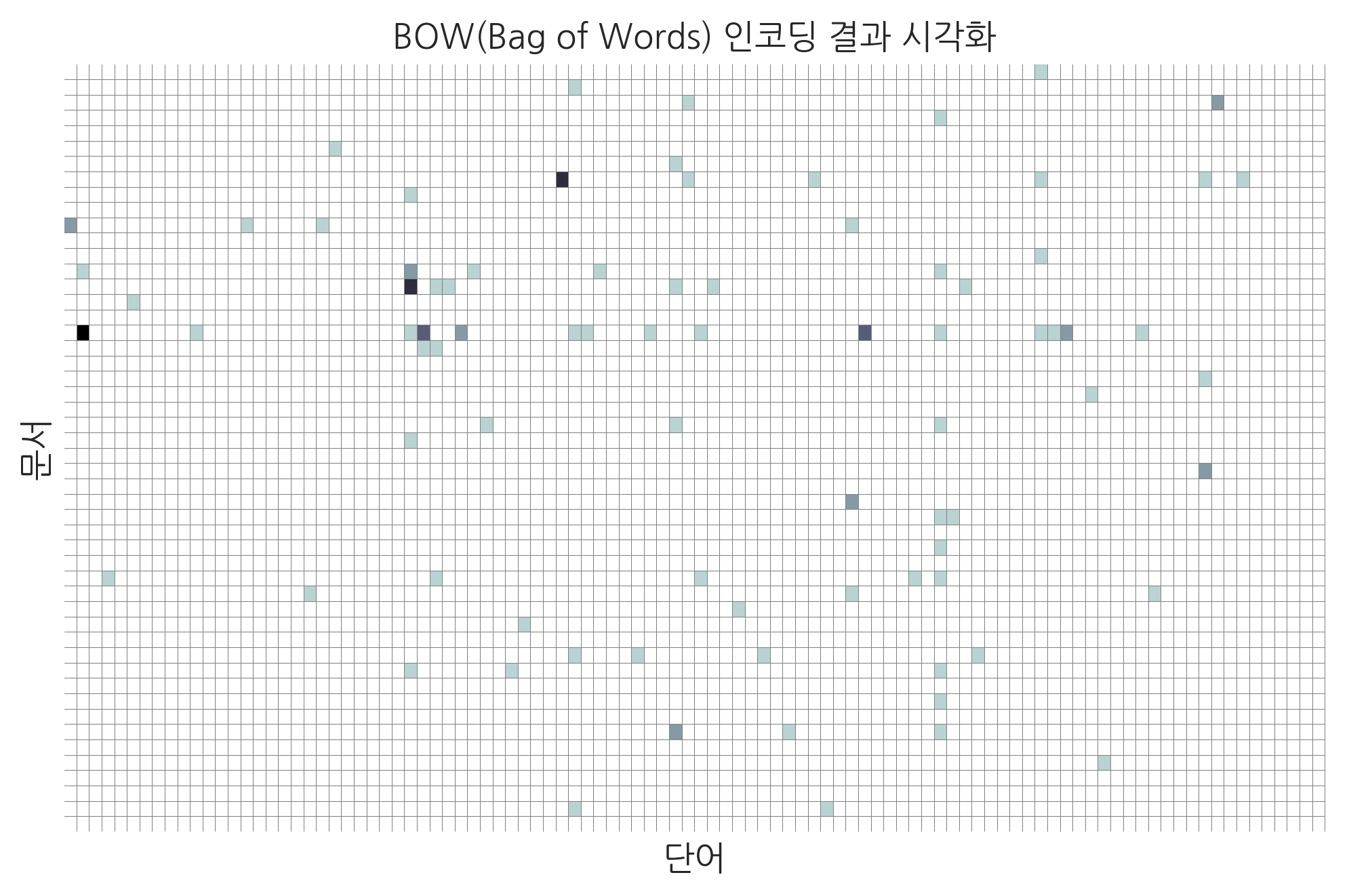
물론 문서 데이터를 숫자로 변환하는 방법은 여기에서 설명한 BOW 외에도 다양하다. 위의 설명은 문서 데이터도 결국은 숫자로 바꾸어야지만 컴퓨터에서 처리할 수 있다는 것을 보여주기위한 한 예일 뿐이다.
카테고리값#
앞에서 컴퓨터가 다룰 수 있는 데이터는 숫자 데이터 뿐이라고 했는데 사실은 한가지 종류의 데이터를 더 다룰 수 있다. 바로 카테고리(category)값 또는 범주형 값이라고 부르는 데이터이다.
카테고리값은 숫자 값과 달리 주로 기호로 표시되며 비연속적이다. 하지만 더 중요한 차이점은 두 개의 데이터가 있을 때 이들의 크기나 가치, 혹은 순서를 비교할 수 있는가 없는가이다. 예를 들어 10kg과 20kg이라는 두 개의 무게는 20이 10보다 “두 배정도 크다”라고 크기를 비교하는 것이 가능하다. 그러나 “고양이”와 “개”라는 두 개의 카테고리값은 크기나 가치를 비교할 수 없다.
일반적으로 카테고리값은 가질 수 있는 경우의 수가 제한되어 있다. 이러한 경우의 수를 ‘클래스(class)’라고 부르는데 동전을 던진 결과와 같이 “앞면(head)” 혹은 “뒷면(tail)”처럼 두 가지 경우만 가능하면 ‘이진 클래스(binary class)’라고 한다. 그리고 주사위를 던져서 나온 숫자와 같이 세 개 이상의 경우가 가능하면 ‘다중 클래스(multi class)’라고 한다.
카테고리값처럼 비연속적이지만 숫자처럼 비교 가능한 경우도 있을 수 있다. 예를 들어 학점을 “A”, “B”, “C”, “D”와 같이 주는 경우는 비연속적이고 기호로 표시되지만, 크기 혹은 순서를 비교할 수 있다. 이러한 경우는 분석의 목표에 따라 숫자로 표기하기도 하고 일반적인 카테고리값으로 표기하기도 한다.
회귀분석과 분류#
예측 문제는 출력하고자 하는 데이터가 숫자 값인가 카테고리값인가에 따라 사용하는 방법이 완전히 달라진다.
출력하고자 하는 값이 숫자인 경우를 **회귀분석(regression analysis)**이라고 하며, 전통적인 통계분석에서 많이 사용하는 예측 방법이다. 반대로 출력하고자 하는 값이 카테고리값인 경우는 **분류(classification)**라고 부른다. 머신러닝 방법은 대부분 이러한 분류 문제를 풀기위한 방법이다.
분류 문제는 우리가 푸는 시험문제 중 4지 선다형 객관식 문제와 같은 것으로 생각할 수 있다. 반대로 회귀 분석은 답이 되는 숫자를 직접 써야 하는 단답형 문제라고 할 수 있다.
예를 들어 이미지를 컴퓨터에 입력했을 때 “개”인지 “고양이”인지 판별하는 문제는 사실 내부적으로 분류 문제를 사용한다. 보통 1,000개 혹은 그 이상의 가능한 이미지 카테고리 목록을 준비하고 해당 이미지가 이 카테고리에서 어떤 것에 해당하는지를 찾아내는 1,000지 선다형 객관식 문제와 같은 것이다.
연습 문제 1.1.7#
지금까지 고려했던 예측 문제의 입력 데이터와 출력 데이터가 각각 숫자 값인지 카테고리값인지 쓰고 문제가 회귀분석 문제인지 분류 문제인지 결정하라.
회귀분석의 예#
다음은 회귀분석의 한 예로 scikit-learn 패키지에서 제공하는 주택가격을 예측하는 문제를 보였다. 이 문제는 범죄율, 공기 오염도 등의 주거 환경 정보 등을 사용하여 70년대 미국 보스턴시의 주택가격을 예측하는 문제이다.
보스턴 주택가격 데이터
from sklearn.datasets import load_boston
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["주택가격"] = boston.target
g = sns.pairplot(df[["주택가격", "RM", "AGE", "CRIM"]])
g.fig.suptitle("보스턴 주택가격 데이터 일부 (RM: 방 개수, AGE: 노후화, CRIM: 범죄율)", y=1.02)
plt.show()
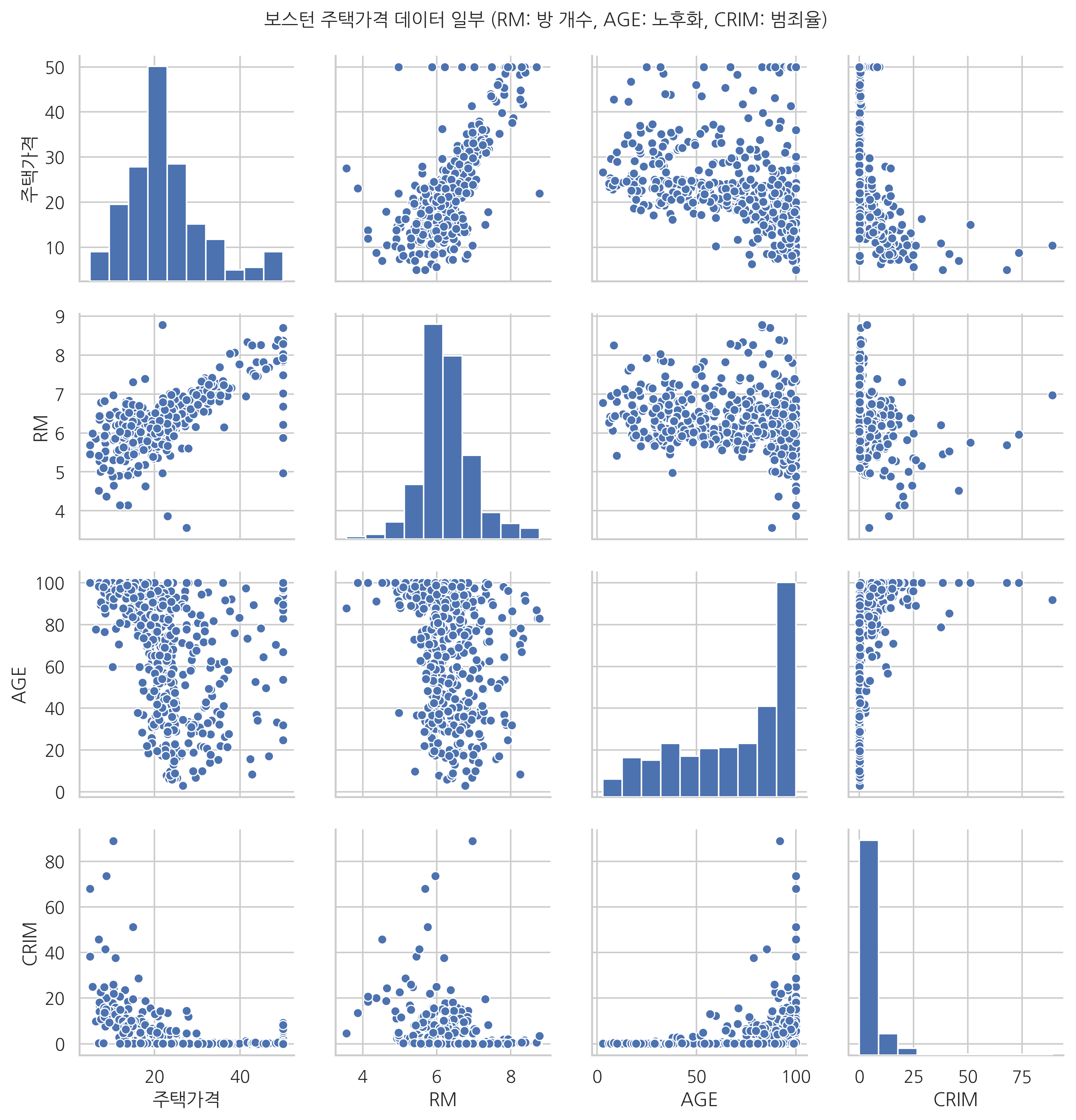
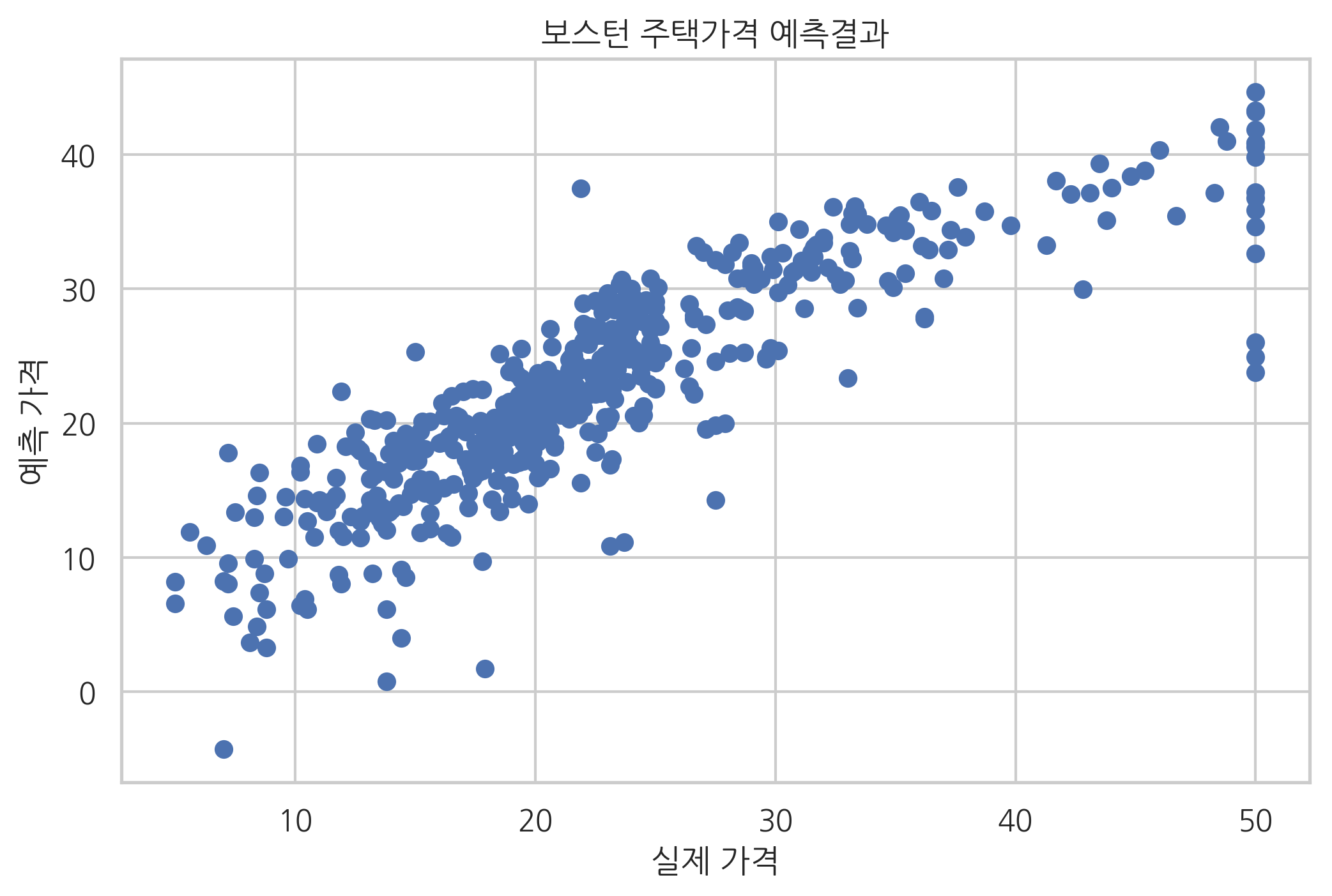
이 문제를 회귀분석 방법으로 풀면 다음 결과 그래프와 같다. 결과 그래프에서 하나의 점은 하나의 데이터를 뜻한다. 점의 가로축 값은 실제 가격을 나타내고 세로축 값은 회귀분석 결과이다. 만약 회귀분석 방법으로 가격을 정확하게 예측했다면 결과는 기울기가 1인 직선과 같은 형태가 되어야 하지만 실제로는 타원 모양이 되는 경우가 많다.
보스턴 주택가격 예측결과
from sklearn.linear_model import LinearRegression
model = LinearRegression().fit(boston.data, boston.target)
predicted = model.predict(boston.data)
plt.scatter(boston.target, predicted)
plt.xlabel("실제 가격")
plt.ylabel("예측 가격")
plt.title("보스턴 주택가격 예측결과")
plt.show()
분류의 예#
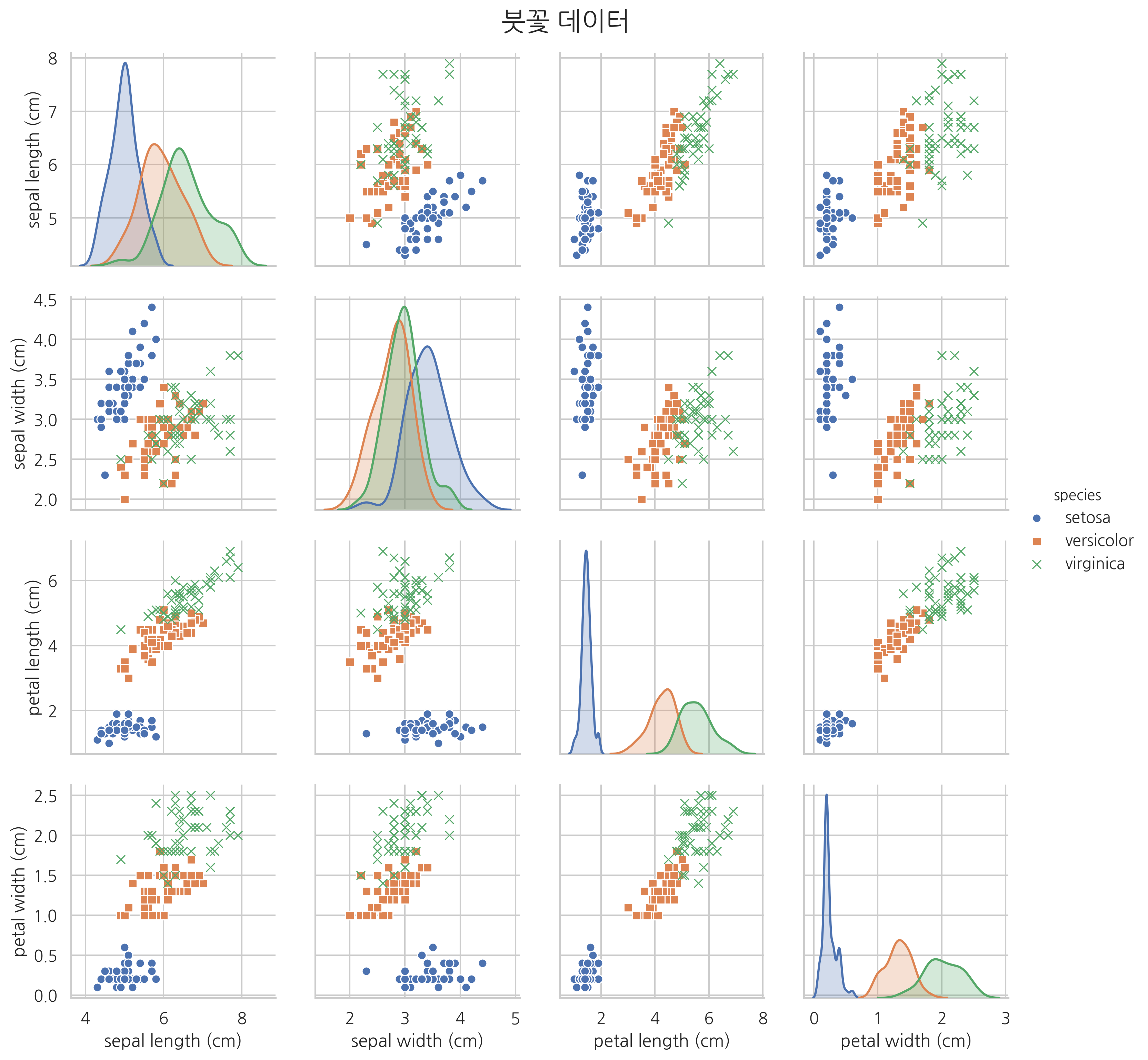
다음은 분류의 한 예로 scikit-learn 패키지에서 제공하는 붓꽃(iris) 분류 문제를 보였다. 이 문제는 붓꽃의 꽃받침 길이(sepal length), 꽃받침 폭(sepal width), 꽃잎 길이(petal length), 꽃잎 폭(petal width)을 이용하여 붓꽃의 세가지 종류(setosa, versicolor, virginica) 중 어느 것에 속하는지를 결정하는 문제이다.
아래에는 파이썬을 이용하여 붓꽃 데이터의 일부와 이를 시각화한 모습을 보였다.
붓꽃 분류 데이터
from sklearn.datasets import load_iris
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
sy = pd.Series(iris.target, dtype="category")
sy = sy.cat.rename_categories(iris.target_names)
df['species'] = sy
np.random.seed(0)
df.sample(frac=1).reset_index(drop=True).head(10)
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | species | |
|---|---|---|---|---|---|
| 0 | 5.8 | 2.8 | 5.1 | 2.4 | virginica |
| 1 | 6.0 | 2.2 | 4.0 | 1.0 | versicolor |
| 2 | 5.5 | 4.2 | 1.4 | 0.2 | setosa |
| 3 | 7.3 | 2.9 | 6.3 | 1.8 | virginica |
| 4 | 5.0 | 3.4 | 1.5 | 0.2 | setosa |
| 5 | 6.3 | 3.3 | 6.0 | 2.5 | virginica |
| 6 | 5.0 | 3.5 | 1.3 | 0.3 | setosa |
| 7 | 6.7 | 3.1 | 4.7 | 1.5 | versicolor |
| 8 | 6.8 | 2.8 | 4.8 | 1.4 | versicolor |
| 9 | 6.1 | 2.8 | 4.0 | 1.3 | versicolor |
sns.pairplot(df, hue="species", markers=["o", "s", "x"])
plt.suptitle("붓꽃 데이터", y=1.02, fontsize=18)
plt.show()
이 문제를 서포트 벡터 머신(SVC: Support Vector Machine)이라는 분류 모형으로 풀면 다음과 같다.
붓꽃 분류 문제를 서포트 벡터 머신으로 푼 결과
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
features = [2, 3]
X = iris.data[:, features]
y = iris.target
model = SVC(kernel="linear", random_state=0)
model.fit(X, y)
XX_min = X[:, 0].min() - 1
XX_max = X[:, 0].max() + 1
YY_min = X[:, 1].min() - 1
YY_max = X[:, 1].max() + 1
XX, YY = np.meshgrid(np.linspace(XX_min, XX_max, 1000),
np.linspace(YY_min, YY_max, 1000))
ZZ = model.predict(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
cmap = mpl.colors.ListedColormap(['seashell', 'lightgreen', 'lightskyblue'])
plt.contourf(XX, YY, ZZ, cmap=cmap)
plt.contour(XX, YY, ZZ, colors='k')
plt.scatter(X[y == 0, 0], X[y == 0, 1], s=20, label=iris.target_names[0],
marker="o", edgecolors="darkred", facecolors="red")
plt.scatter(X[y == 1, 0], X[y == 1, 1], s=20, label=iris.target_names[1],
marker="s", edgecolors="darkgreen", facecolors="green")
plt.scatter(X[y == 2, 0], X[y == 2, 1], s=30, label=iris.target_names[2],
marker="x", edgecolors="darkblue", facecolors="blue")
plt.xlim(XX_min, XX_max)
plt.ylim(YY_min, YY_max)
plt.xlabel("꽃잎의 길이(cm)")
plt.ylabel("꽃잎의 폭(cm)")
plt.title("서포트벡터머신을 이용한 붓꽃 분류 결과")
plt.legend(loc="lower right", framealpha=1)
plt.show()
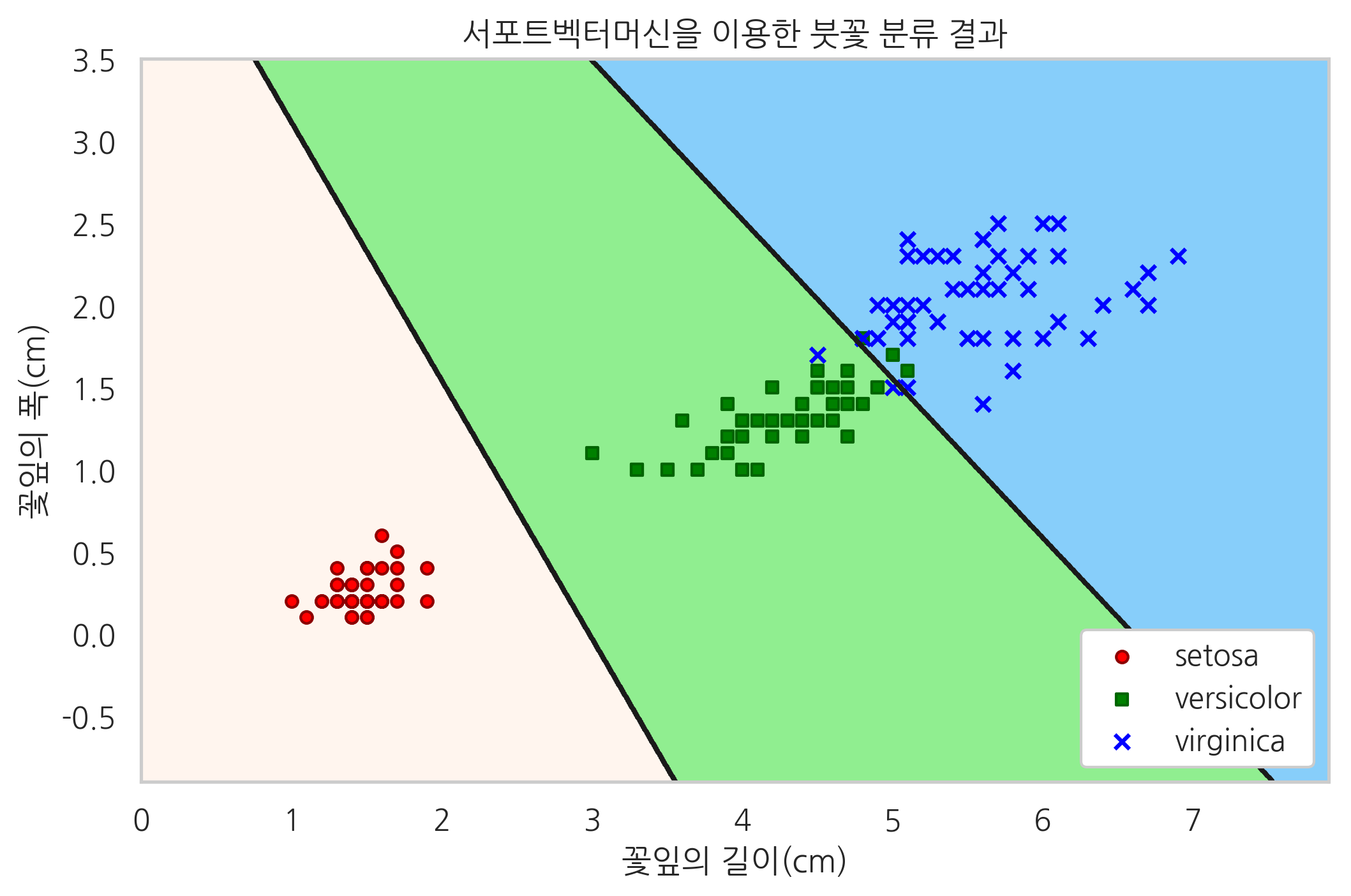
이 그림에서 하나의 점은 하나의 표본 데이터를 가리키고, 다른 색으로 칠해진 영역은 서포트 벡터 머신이 다른 종으로 분류하고 있는 영역을 뜻한다.
비지도학습#
지금까지 살펴본 지도학습에서는 입력값과 출력값의 쌍(pair)을 학습데이터로 하여 입력값에 대한 출력값을 예측하도록 학습을 시켰다. 하지만 때로는 데이터간에 입력과 출력의 관계가 명확하지 않을 수도 있다. 이렇게 입력/출력이 구분되지 않는 단순한 “데이터들의 관계”에서 특정한 규칙을 찾아내는 것을 **비지도학습(unsupervised learning)**이라고 한다. 비지도학습에서는 입력/출력 데이터를 구분짓지 않고 단순히 데이터를 입력하면 이 데이터들간의 규칙을 찾아내거나 미리 지정한 규칙(모형)에 맞는 데이터인지를 구분해 낸다.
클러스터링#
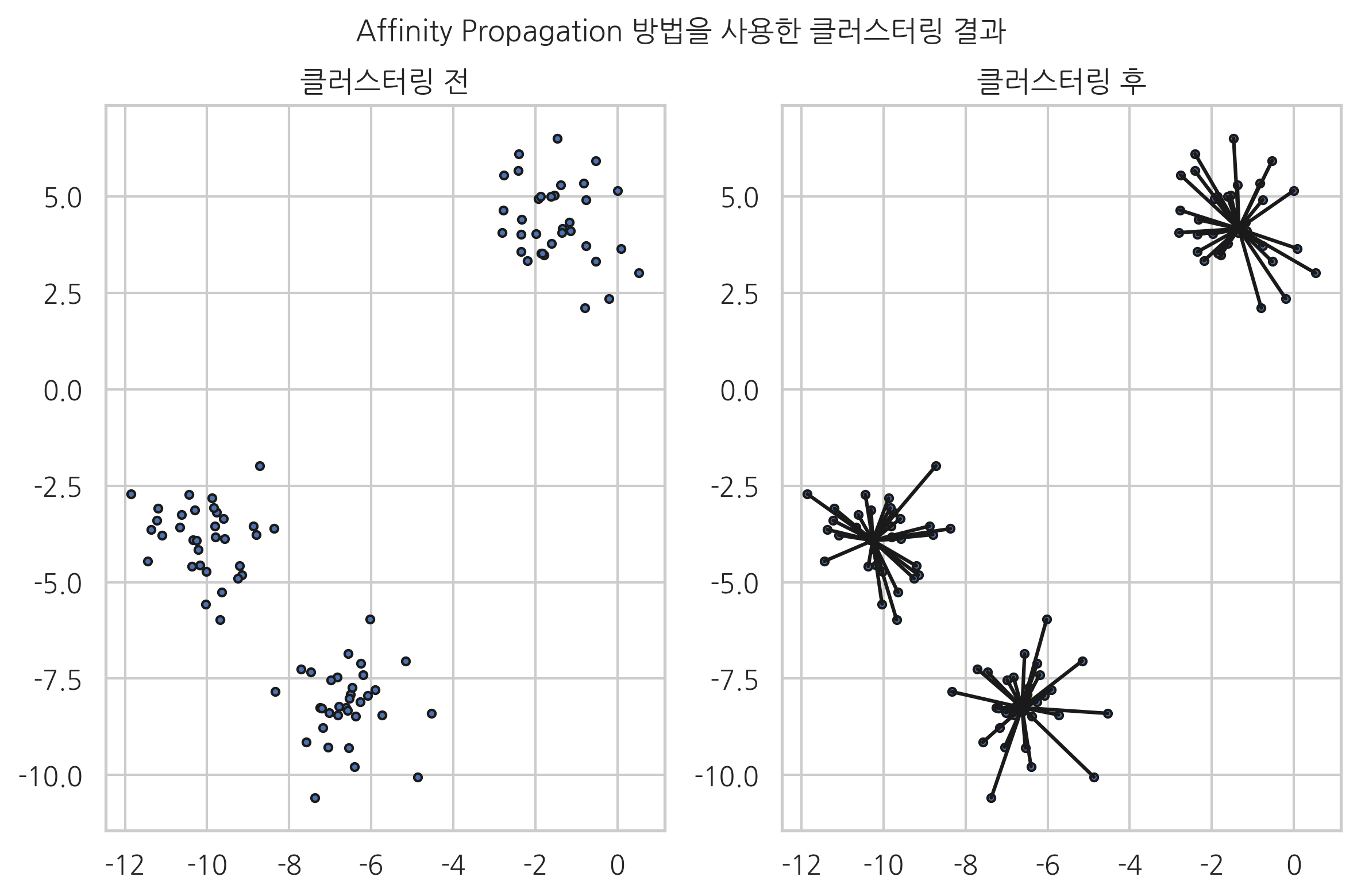
대표적인 비지도학습 방법 중 하나는 데이터들을 유사한 데이터까지 같은 그룹으로 모으는 클러스터링(clustering) 방법이다. 다음 예제는 100개의 2차원 데이터들을 affinity propagation이라는 방법으로 클러스터링한 결과이다. 왼쪽 그림은 클러스터링을 하기 전의 데이터들을 나타낸 것이고 오른쪽 그림은 클러스터링으로 모아진 데이터를 나타낸 것이다. 전체 데이터를 3개의 그룹으로 분리할 수 있다는 것을 알 수 있다.
클러스터링 예제
from sklearn.datasets import make_blobs
from sklearn.cluster import AffinityPropagation
X, _ = make_blobs(n_features=2, centers=3, random_state=1)
model = AffinityPropagation().fit(X)
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], marker='o', s=10, edgecolor="k")
plt.title("클러스터링 전")
plt.subplot(122)
plt.scatter(X[:, 0], X[:, 1], marker='o', s=10, edgecolor="k")
plt.title("클러스터링 후")
for k in range(3):
cluster_center = X[model.cluster_centers_indices_[k]]
for x in X[model.labels_ == k]:
plt.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], c="k")
plt.suptitle("Affinity Propagation 방법을 사용한 클러스터링 결과", y=1.03)
plt.tight_layout()
plt.show()