5.3 레버리지와 아웃라이어#
레버리지#
개별적인 데이터 표본 하나하나가 회귀분석 결과에 미치는 영향력은 레버리지 분석이나 아웃라이어 분석을 통해 알 수 있다.
**레버리지(leverage)**는 실제 종속변수값 \(y\)가 예측치(predicted target) \(\hat{y}\)에 미치는 영향을 나타낸 값이다. self-influence, self-sensitivity 라고도 한다.
가중치 벡터의 결과값을 예측식에 대입하여 \(y\) 와 \(\hat{y}\)의 관계를 다음과 같다는 것을 보였었다.
이 행렬 \(H\)를 영향도 행렬(influence matrix) 또는 hat 행렬(hat matrix)이라고 한다고 하였다.
행렬 \(H\)의 \(i\)번째 행, \(j\)번째 열 성분을 \(h_{ij}\)라고 하면 실제 결과값 \(y_i\)과 예측값 \(\hat{y}_i\)은 다음과 같은 관계를 가진다.
레버리지는 수학적으로 **영향도 행렬의 대각성분 \(h_{ii}\)**으로 정의된다. 즉, 레버리지는 실제의 결과값 \(y_i\)이 예측값 \(\hat{y}_i\)에 미치는 영향, 즉 예측점을 자기 자신의 위치로 끌어 당기는 정도를 나타낸 것이다.
만약 \(h_{ii}\) 값이 1이 되고 나머지 성분들이 모두 0이 될 수만 있다면 모든 표본 데이터에 대해 실제 결과값과 예측값이 일치하게 될 것이다.
하지만 곧 알 수 있듯이 이러한 일은 발생하지 않는다. 레버리지값은 다음과 같은 특성을 가진다는 것을 수학적으로 증명할 수 있다.
1보다 같거나 작은 양수 혹은 0이다.
\[ 0 \leq h_{ii} \leq 1 \]레버리지의 합은 모형에 사용된 모수의 갯수 \(K\)와 같다. 모수에는 상수항도 포함되므로 상수항이 있는 1차원 모형에서는 \(K = 2\)가 된다.
\[ \text{tr}(H) = \sum_i^N h_{ii} = K \]
이 두가지 성질로부터 레버리지 값은 \(N\)개의 데이터에 대한 레버리지값은 양수이고 그 합이 \(K\)가 된다는 것을 알 수 있다. 즉 \(K\)라고 하는 값을 \(N\)개의 변수가 나누어 가지는 것과 같다. 현실적으로 데이터의 갯수 \(N\)는 모수의 갯수 \(K\)보다 훨씬 많기 때문에 위에서 말한 특성을 적용하면 모든 레버리지 값이 동시에 1이 되는 것은 불가능하다.
위 식을 이용하면 레버리지의 평균값도 구할 수 있다.
보통 이 평균값의 2 ~ 4배보다 레버리지 값이 크면 레버리지가 크다고 이야기한다.
statsmodels를 이용한 레버리지 계산#
레버리지 값은 RegressionResults 클래스의 get_influence 메서드로 다음과 같이 구할 수 있다. 우선 다음과 같은 가상의 1차 데이터로 회귀분석 예제를 풀어보자.
from sklearn.datasets import make_regression
# 100개의 데이터 생성
X0, y, coef = make_regression(n_samples=100, n_features=1, noise=20,
coef=True, random_state=1)
# 레버리지가 높은 가상의 데이터를 추가
data_100 = (4, 300)
data_101 = (3, 150)
X0 = np.vstack([X0, np.array([data_100[:1], data_101[:1]])])
X = sm.add_constant(X0)
y = np.hstack([y, [data_100[1], data_101[1]]])
plt.scatter(X0, y)
plt.xlabel("x")
plt.ylabel("y")
plt.title("가상의 회귀분석용 데이터")
plt.show()
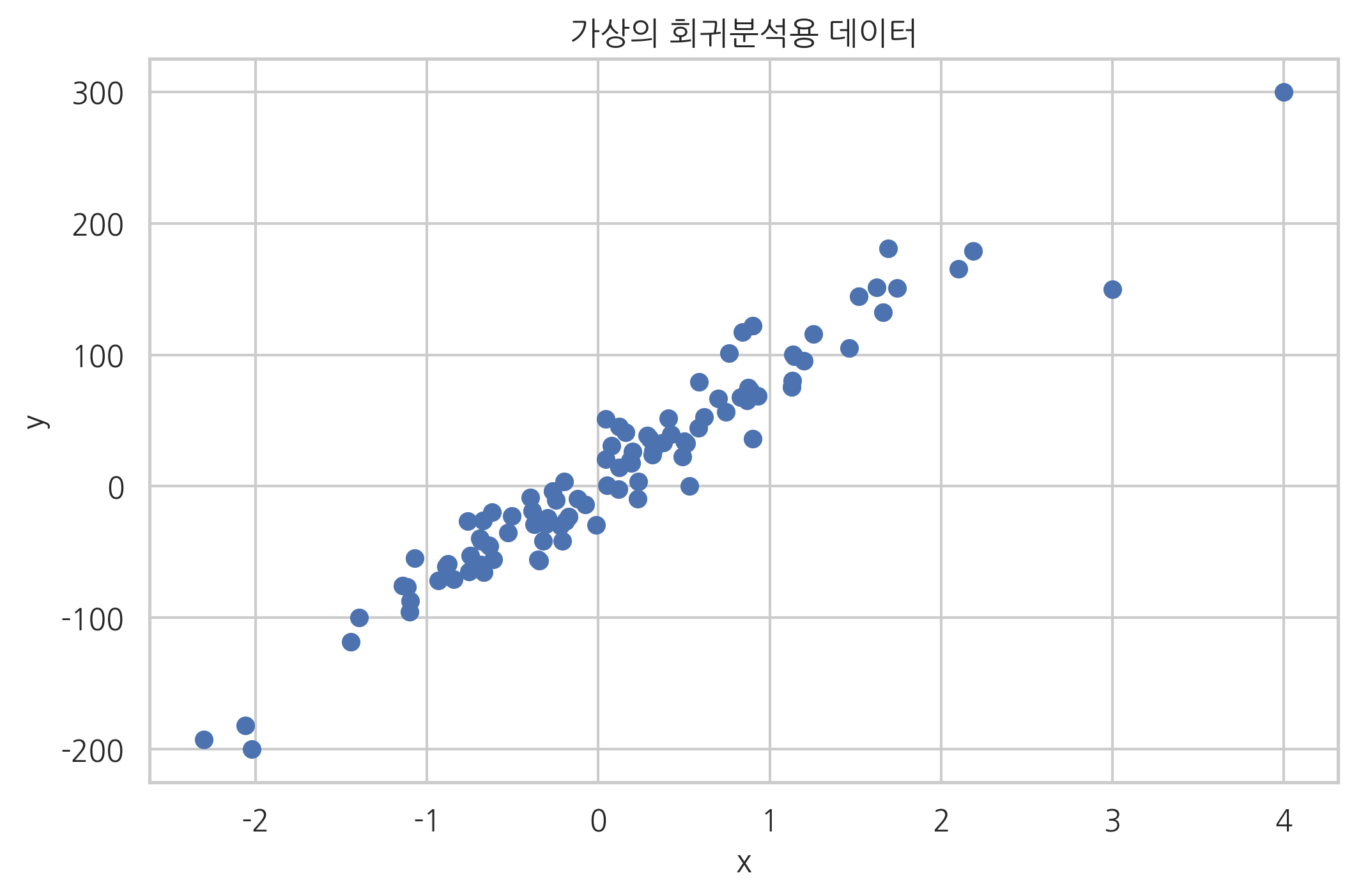
이 데이터를 이용하여 선형회귀를 한 결과는 다음과 같다.
model = sm.OLS(pd.DataFrame(y), pd.DataFrame(X))
result = model.fit()
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: 0 R-squared: 0.936
Model: OLS Adj. R-squared: 0.935
Method: Least Squares F-statistic: 1464.
Date: Fri, 19 Apr 2019 Prob (F-statistic): 1.61e-61
Time: 09:35:48 Log-Likelihood: -452.71
No. Observations: 102 AIC: 909.4
Df Residuals: 100 BIC: 914.7
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
0 3.2565 2.065 1.577 0.118 -0.840 7.353
1 78.3379 2.048 38.260 0.000 74.276 82.400
==============================================================================
Omnibus: 16.191 Durbin-Watson: 1.885
Prob(Omnibus): 0.000 Jarque-Bera (JB): 36.807
Skew: -0.534 Prob(JB): 1.02e-08
Kurtosis: 5.742 Cond. No. 1.14
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
선형회귀 결과에서 get_influence 메서드를 호출하면 영향도 정보 객체를 구할 수 있다. 이 객체는 hat_matrix_diag 속성으로 레버리지 벡터의 값을 가지고 있다.
influence = result.get_influence()
hat = influence.hat_matrix_diag
plt.figure(figsize=(10, 2))
plt.stem(hat)
plt.axhline(0.02, c="g", ls="--")
plt.title("각 데이터의 레버리지 값")
plt.show()
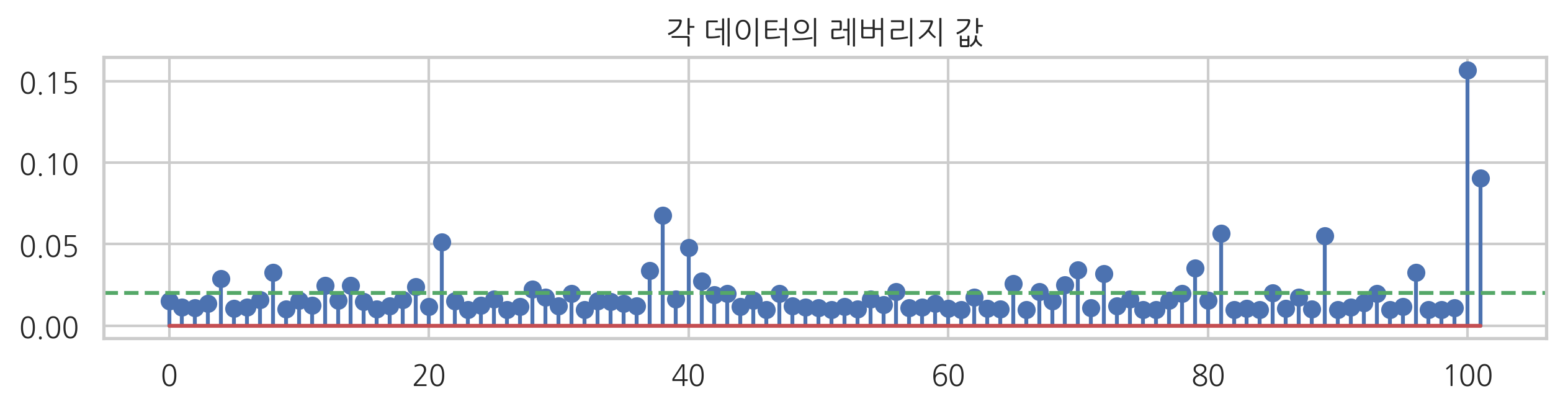
수동으로 추가한 마지막 두 개의 데이터를 제외하면 대부분의 데이터는 레버리지 값이 0.02 근처의 낮은 값을 가진다.
레버리지의 합이 2와 같아진다는 것도 다음과 같이 확인할 수 있다.
hat.sum()
2.0000000000000004
위 결과를 이용하여 레버리지가 큰 데이터만 표시하면 아래와 같다. 여기에서는 레버리지 값이 0.05를 넘는 데이터만 큰 원으로 표시하였다.
ax = plt.subplot()
plt.scatter(X0, y)
sm.graphics.abline_plot(model_results=result, ax=ax)
idx = hat > 0.05
plt.scatter(X0[idx], y[idx], s=300, c="r", alpha=0.5)
plt.title("회귀분석 결과와 레버리지 포인트")
plt.show()
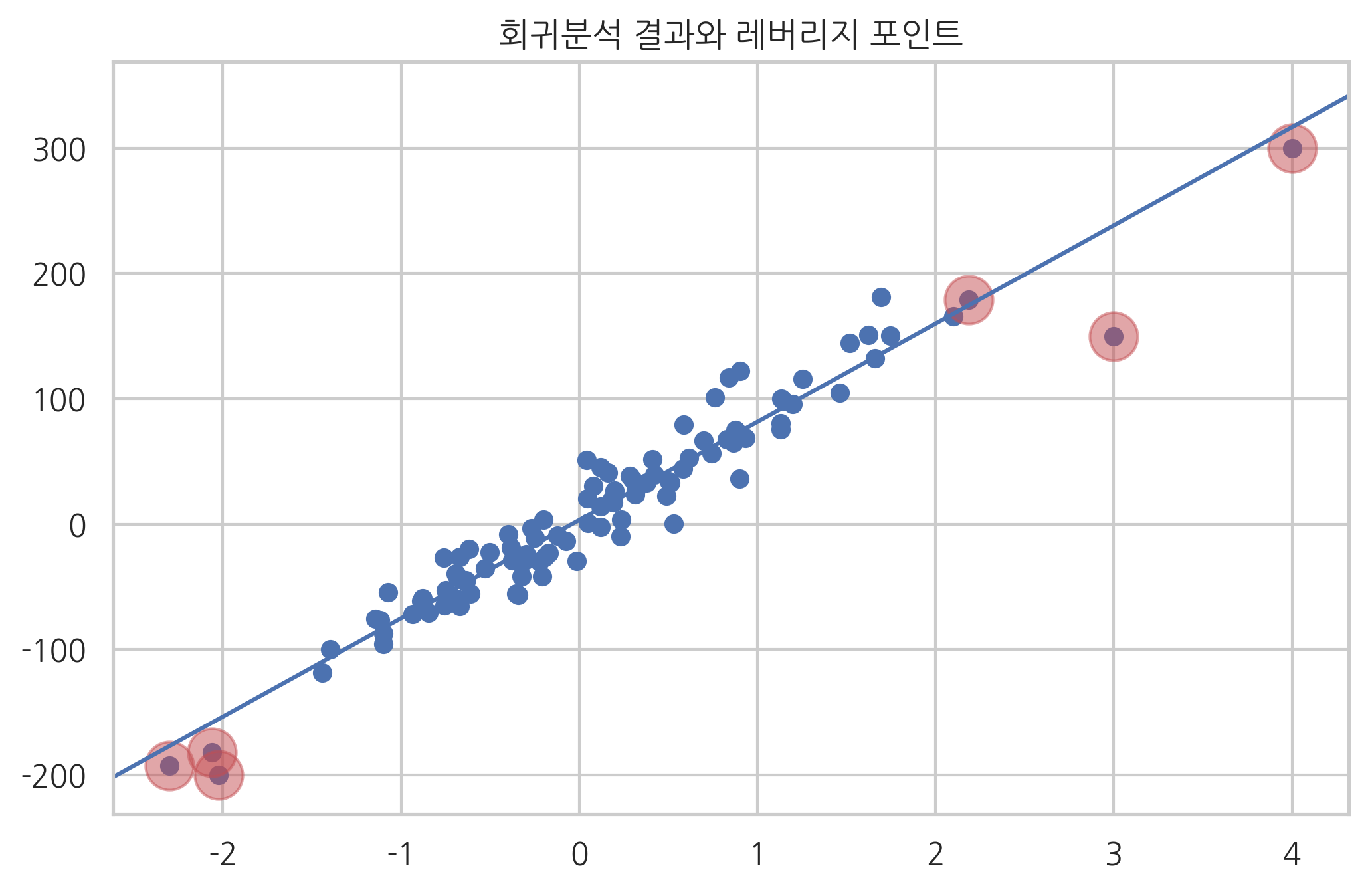
위 그림에서 데이터가 무리지어 있지 않고 단독으로 존재할수록 레버리지가 커짐을 알 수 있다.
레버리지의 영향#
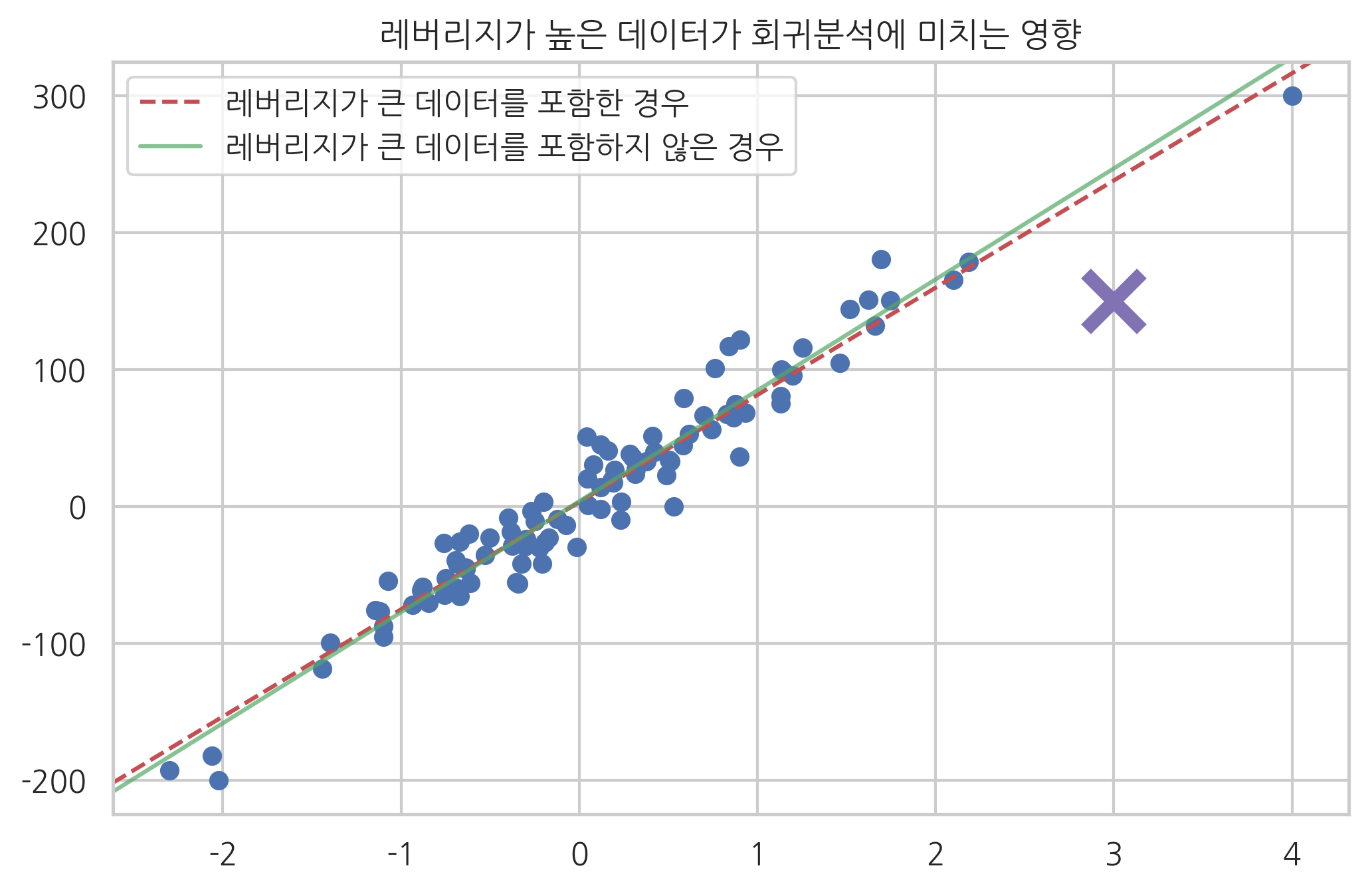
레버리지가 큰 데이터가 모형에 주는 영향을 보기 위해 이 데이터가 포함된 경우의 모형과 포함되지 않은 경우의 모형을 아래에 비교하였다. 레버리지가 큰 데이터는 포함되거나 포함되지 않는가에 따라 모형에 주는 영향이 큰 것을 알 수 있다.
model2 = sm.OLS(y[:-1], X[:-1])
result2 = model2.fit()
ax = plt.subplot()
plt.scatter(X0, y)
sm.graphics.abline_plot(model_results=result,
c="r", linestyle="--", ax=ax)
sm.graphics.abline_plot(model_results=result2,
c="g", alpha=0.7, ax=ax)
plt.plot(X0[-1], y[-1], marker='x', c="m", ms=20, mew=5)
plt.legend([u"레버리지가 큰 데이터를 포함한 경우", u"레버리지가 큰 데이터를 포함하지 않은 경우"],
loc="upper left")
plt.title("레버리지가 높은 데이터가 회귀분석에 미치는 영향")
plt.show()
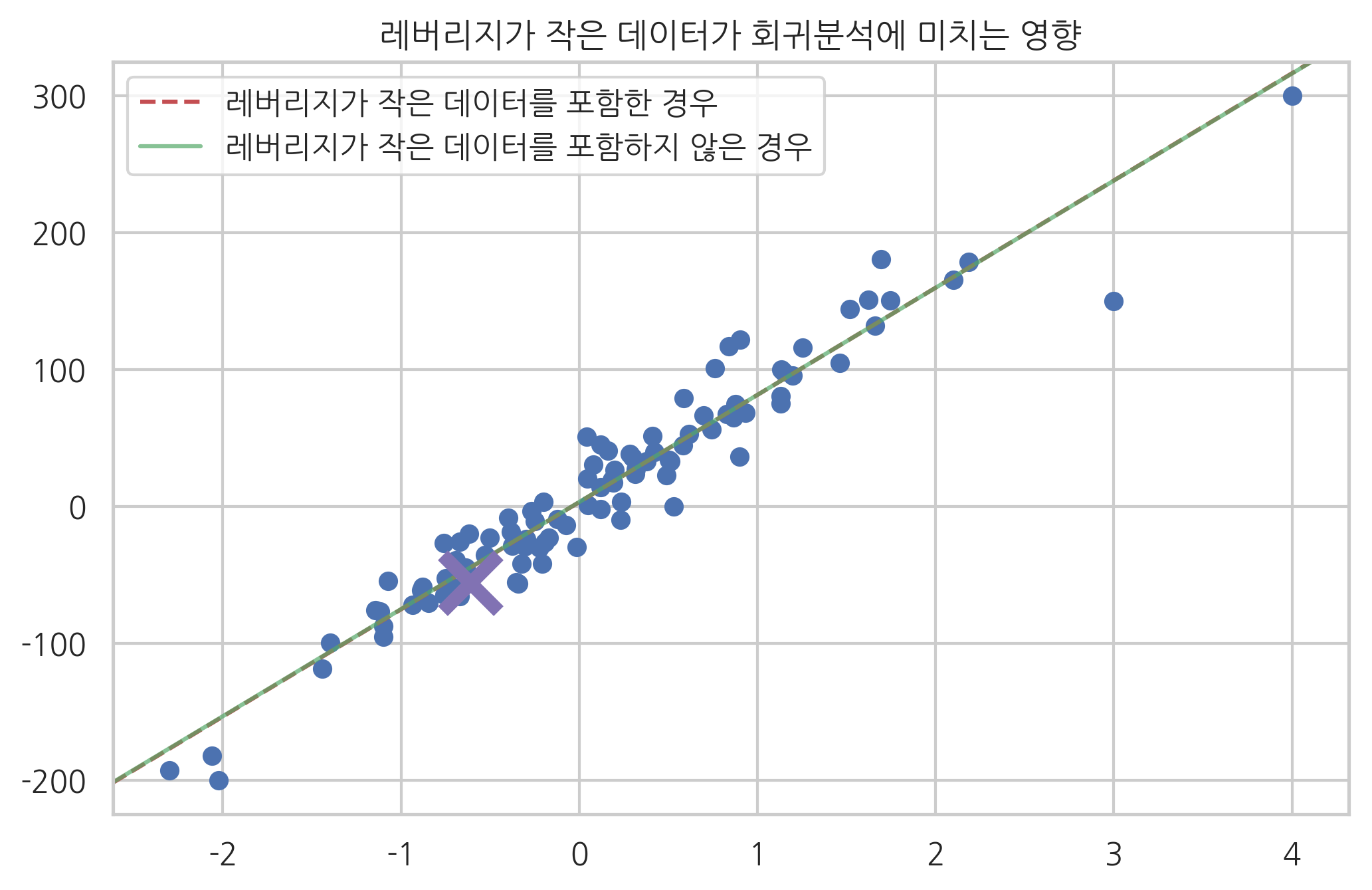
반대로 레버리지가 작은 데이터는 포함되거나 포함되지 않거나 모형이 별로 달라지지 않는 것을 알 수 있다.
model3 = sm.OLS(y[1:], X[1:])
result3 = model3.fit()
ax = plt.subplot()
plt.scatter(X0, y)
sm.graphics.abline_plot(model_results=result,
c="r", linestyle="--", ax=ax)
sm.graphics.abline_plot(model_results=result3,
c="g", alpha=0.7, ax=ax)
plt.plot(X0[0], y[0], marker='x', c="m", ms=20, mew=5)
plt.legend([u"레버리지가 작은 데이터를 포함한 경우", u"레버리지가 작은 데이터를 포함하지 않은 경우"],
loc="upper left")
plt.title("레버리지가 작은 데이터가 회귀분석에 미치는 영향")
plt.show()
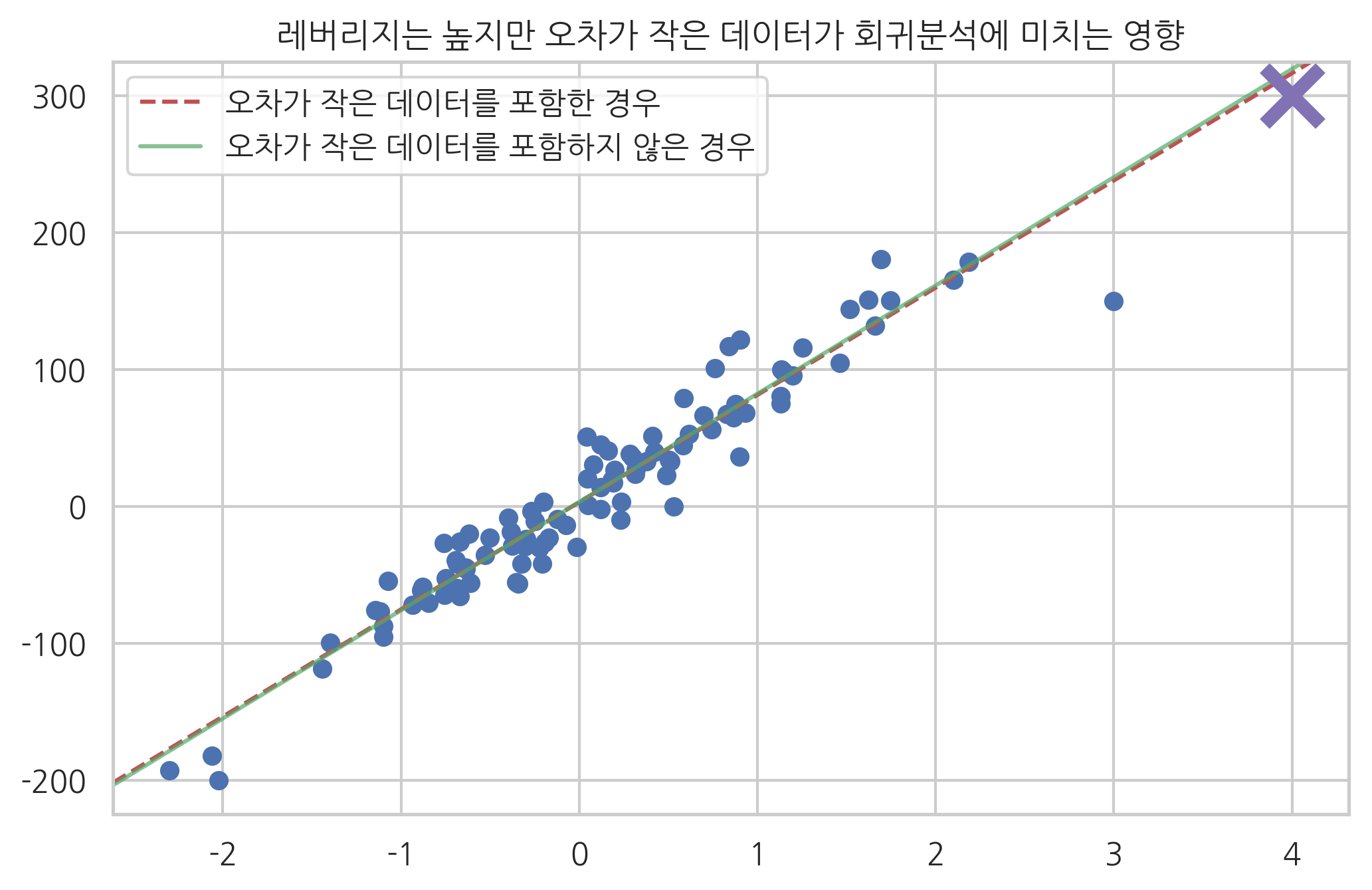
혹은 레버리지가 크더라도 오차가 작은 데이터는 포함되거나 포함되지 않거나 모형이 별로 달라지지 않는다.
idx = np.array(list(range(100)) + [101])
model4 = sm.OLS(y[idx], X[idx, :])
result4 = model4.fit()
ax = plt.subplot()
plt.scatter(X0, y)
sm.graphics.abline_plot(model_results=result,
c="r", linestyle="--", ax=ax)
sm.graphics.abline_plot(model_results=result4,
c="g", alpha=0.7, ax=ax)
plt.plot(X0[-2], y[-2], marker='x', c="m", ms=20, mew=5)
plt.legend([u"오차가 작은 데이터를 포함한 경우", u"오차가 작은 데이터를 포함하지 않은 경우"],
loc="upper left")
plt.title("레버리지는 높지만 오차가 작은 데이터가 회귀분석에 미치는 영향")
plt.show()
아웃라이어#
모형에서 설명하고 있는 데이터와 동떨어진 값을 가지는 데이터, 즉 잔차가 큰 데이터를 **아웃라이어(outlier)**라고 한다. 그런데 잔차의 크기는 독립 변수의 영향을 받으므로 아웃라이어를 찾으러면 이 영향을 제거한 표준화된 잔차를 계산해야 한다.
표준화 잔차#
개별적인 잔차의 표준편차를 구하면 다음과 같다.
위 식에서는 \(M\)이 대칭 행렬이고 \(M^2=M\)라는 사실을 이용하었다.
대각 성분만 보면 개별적인 잔차의 표준편차는 다음과 같다.
즉, 오차의 표준 편차는 모든 표본에 대해 같지만 개별적인 잔차의 표준편차는 레버리지에 따라 달라지는 것을 알 수 있다.
오차의 분산은 알지 못하므로 잔차 분산으로부터 추정한다.
이 식에서 \(s\)는 다음과 같이 구한 오차의 표준편차 추정값이다.
잔차를 레버리지와 잔차의 표준 편차로 나누어 동일한 표준 편차를 가지도록 스케일링한 것을 표준화 잔차(standardized residual 또는 normalized residual 또는 studentized residual)라고 한다.
statsmodels를 이용한 표준화 잔차 계산#
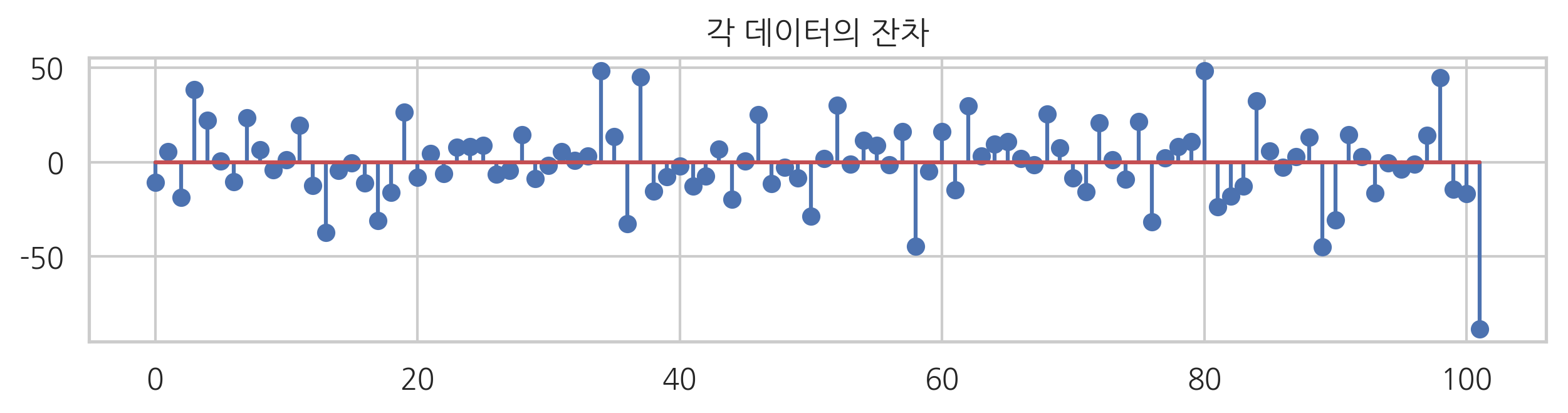
아래에서는 각 데이터의 잔차를 표시하였다. 잔차는 RegressionResult 객체의 resid 속성에 있다.
plt.figure(figsize=(10, 2))
plt.stem(result.resid)
plt.title("각 데이터의 잔차")
plt.show()
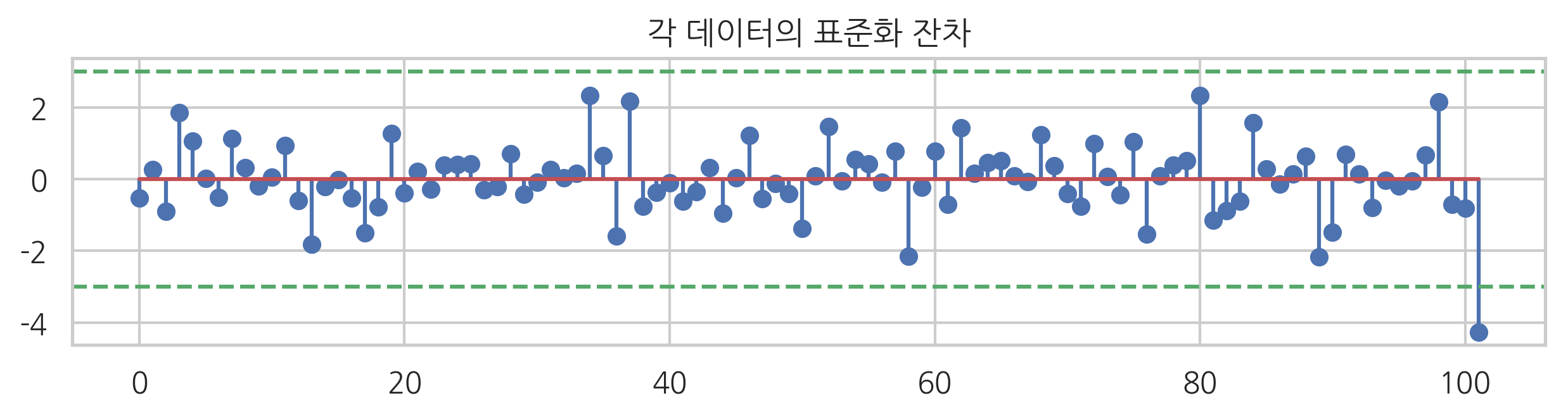
표준화 잔차는 resid_pearson 속성에 있다. 보통 표준화 잔차가 2~4보다 크면 아웃라이어로 본다.
plt.figure(figsize=(10, 2))
plt.stem(result.resid_pearson)
plt.axhline(3, c="g", ls="--")
plt.axhline(-3, c="g", ls="--")
plt.title("각 데이터의 표준화 잔차")
plt.show()
Cook’s Distance#
회귀 분석에는 잔차의 크기가 큰 데이터가 아웃라이어가 되는데 이 중에서도 주로 관심을 가지는 것은 레버리지와 잔차의 크기가 모두 큰 데이터들이다. 잔차와 레버리지를 동시에 보기위한 기준으로는 Cook’s Distance가 있다. 다음과 같이 정의되는 값으로 레버리지가 커지거나 잔차의 크기가 커지면 Cook’s Distance 값이 커진다.
Fox’ Outlier Recommendation 은 Cook’s Distance가 다음과 같은 기준값보다 클 때 아웃라이어로 판단하자는 것이다.
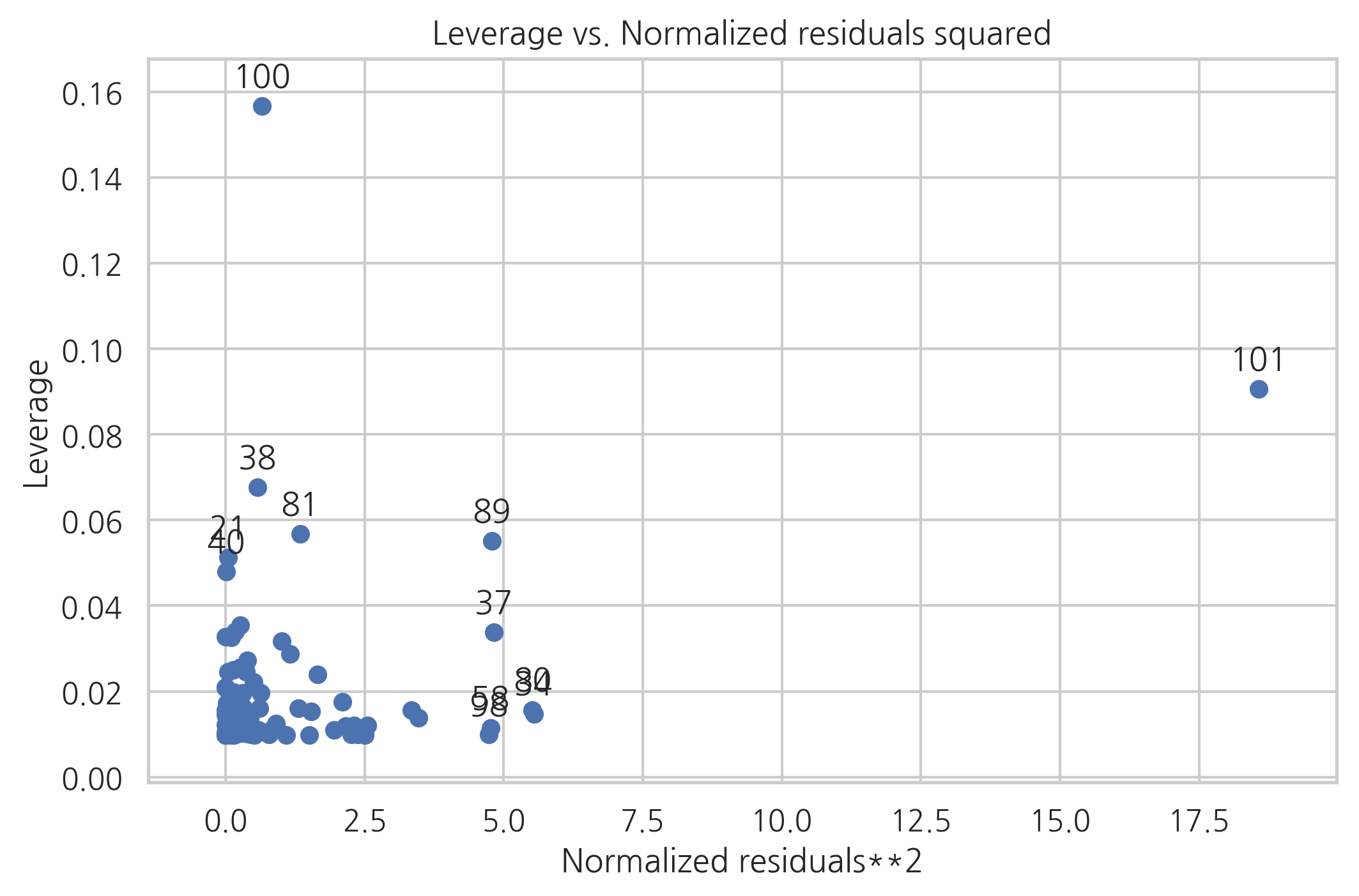
모든 데이터의 레버리지와 잔차를 동시에 보려면 plot_leverage_resid2 명령을 사용한다. 이 명령은 x축으로 표준화 잔차의 제곱을 표시하고 y축으로 레버리지값을 표시한다. 데이터 아이디가 표시된 데이터들이 레버리지가 큰 아웃라이어이다.
sm.graphics.plot_leverage_resid2(result)
plt.show()
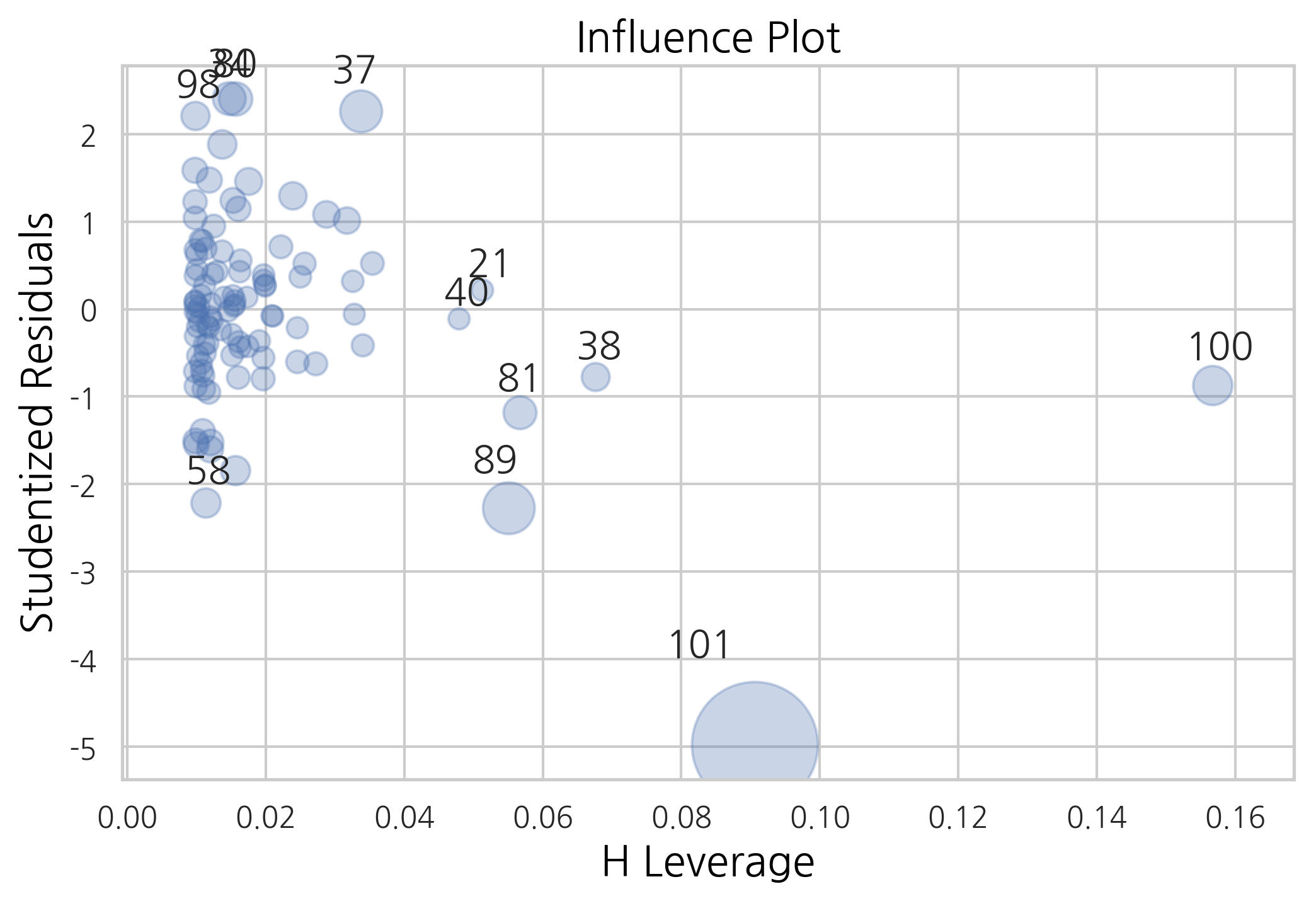
influence_plot 명령을 사용하면 Cook’s distance를 버블 크기로 표시한다.
sm.graphics.influence_plot(result, plot_alpha=0.3)
plt.show()
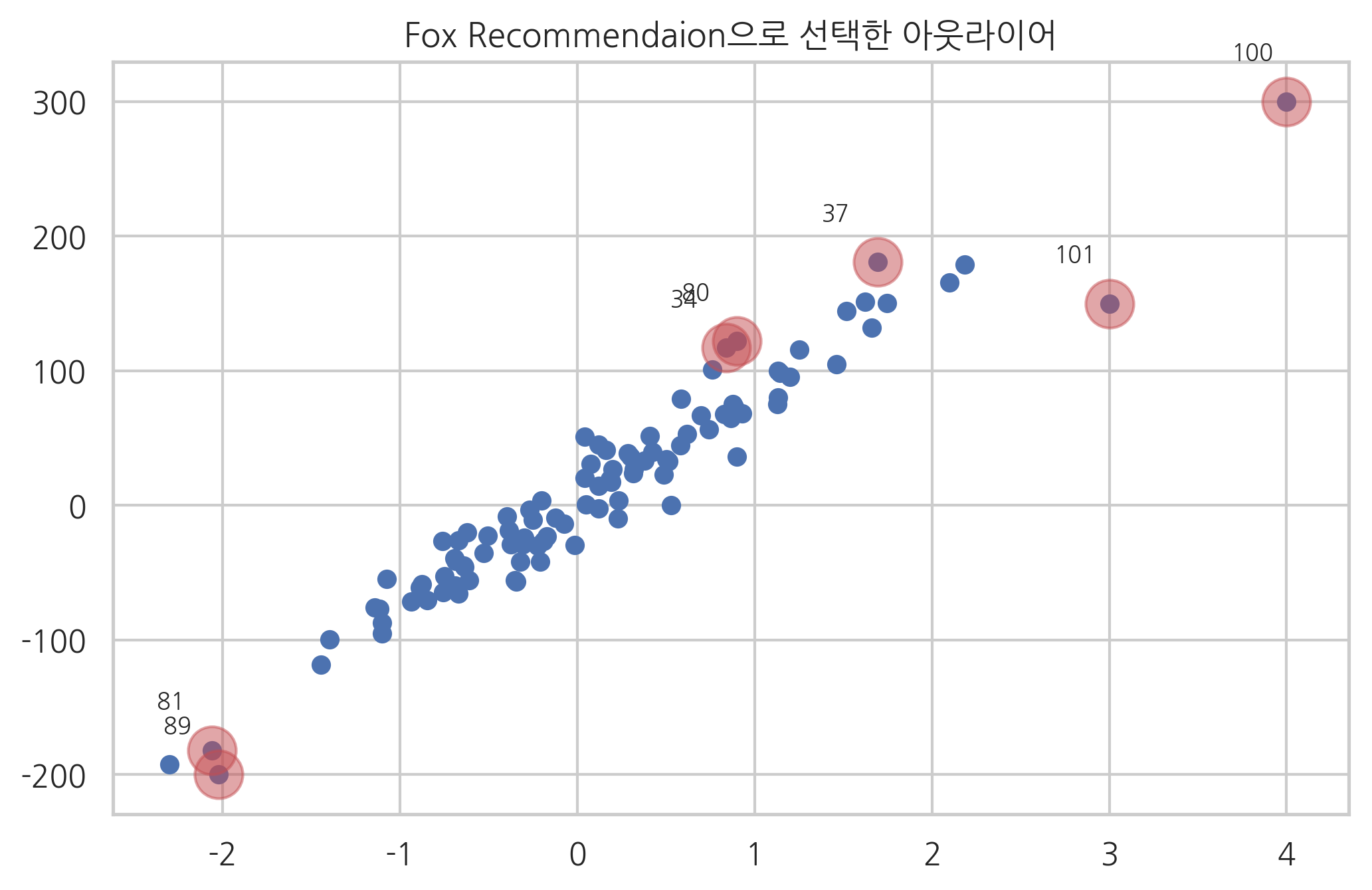
다음 그림은 위에서 사용한 데이터에서 Fox recommentation 기준으로 아웃라이어를 선택한 결과이다.
from statsmodels.graphics import utils
cooks_d2, pvals = influence.cooks_distance
K = influence.k_vars
fox_cr = 4 / (len(y) - K - 1)
idx = np.where(cooks_d2 > fox_cr)[0]
ax = plt.subplot()
plt.scatter(X0, y)
plt.scatter(X0[idx], y[idx], s=300, c="r", alpha=0.5)
utils.annotate_axes(range(len(idx)), idx,
list(zip(X0[idx], y[idx])), [(-20, 15)] * len(idx), size="small", ax=ax)
plt.title("Fox Recommendaion으로 선택한 아웃라이어")
plt.show()
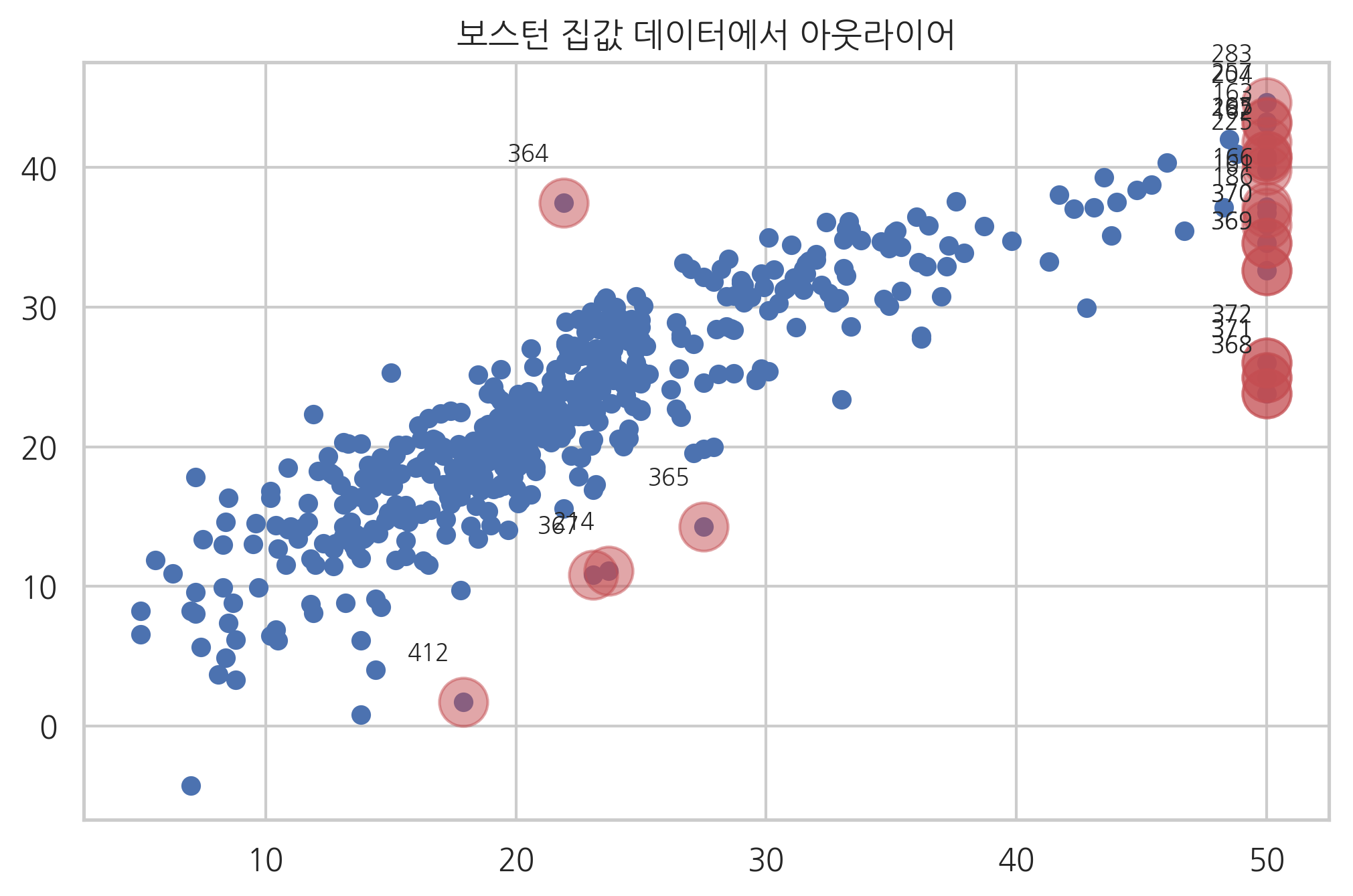
보스턴 집값 예측 문제#
보스턴 집값 문제에 아웃라이어를 적용해 보자. MEDV가 50인 데이터는 상식적으로 생각해도 이상한 데이터이므로 아웃라이어라고 판단할 수 있다. 나머지 데이터 중에서 폭스 추천공식을 사용하여 아웃라이어를 제외한 결과는 다음과 같다.
from sklearn.datasets import load_boston
boston = load_boston()
dfX0 = pd.DataFrame(boston.data, columns=boston.feature_names)
dfX = sm.add_constant(dfX0)
dfy = pd.DataFrame(boston.target, columns=["MEDV"])
model_boston = sm.OLS(dfy, dfX)
result_boston = model_boston.fit()
pred = result_boston.predict(dfX)
influence_boston = result_boston.get_influence()
cooks_d2, pvals = influence_boston.cooks_distance
K = influence.k_vars
fox_cr = 4 / (len(y) - K - 1)
idx = np.where(cooks_d2 > fox_cr)[0]
# MEDV = 50 제거
idx = np.hstack([idx, np.where(boston.target == 50)[0]])
ax = plt.subplot()
plt.scatter(dfy, pred)
plt.scatter(dfy.MEDV[idx], pred[idx], s=300, c="r", alpha=0.5)
utils.annotate_axes(range(len(idx)), idx,
list(zip(dfy.MEDV[idx], pred[idx])), [(-20, 15)] * len(idx), size="small", ax=ax)
plt.title("보스턴 집값 데이터에서 아웃라이어")
plt.show()
다음은 이렇게 아웃라이어를 제외한 후에 다시 회귀분석을 한 결과이다.
idx2 = list(set(range(len(dfX))).difference(idx))
dfX = dfX.iloc[idx2, :].reset_index(drop=True)
dfy = dfy.iloc[idx2, :].reset_index(drop=True)
model_boston2 = sm.OLS(dfy, dfX)
result_boston2 = model_boston2.fit()
print(result_boston2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.812
Model: OLS Adj. R-squared: 0.806
Method: Least Squares F-statistic: 156.1
Date: Fri, 19 Apr 2019 Prob (F-statistic): 2.41e-161
Time: 09:35:52 Log-Likelihood: -1285.2
No. Observations: 485 AIC: 2598.
Df Residuals: 471 BIC: 2657.
Df Model: 13
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 18.8999 4.107 4.602 0.000 10.830 26.969
CRIM -0.0973 0.024 -4.025 0.000 -0.145 -0.050
ZN 0.0278 0.010 2.651 0.008 0.007 0.048
INDUS -0.0274 0.046 -0.595 0.552 -0.118 0.063
CHAS 0.9228 0.697 1.324 0.186 -0.447 2.292
NOX -9.4922 2.856 -3.323 0.001 -15.105 -3.879
RM 5.0921 0.371 13.735 0.000 4.364 5.821
AGE -0.0305 0.010 -2.986 0.003 -0.051 -0.010
DIS -1.0562 0.150 -7.057 0.000 -1.350 -0.762
RAD 0.1990 0.049 4.022 0.000 0.102 0.296
TAX -0.0125 0.003 -4.511 0.000 -0.018 -0.007
PTRATIO -0.7777 0.098 -7.955 0.000 -0.970 -0.586
B 0.0107 0.002 5.348 0.000 0.007 0.015
LSTAT -0.2846 0.043 -6.639 0.000 -0.369 -0.200
==============================================================================
Omnibus: 45.944 Durbin-Watson: 1.184
Prob(Omnibus): 0.000 Jarque-Bera (JB): 65.791
Skew: 0.679 Prob(JB): 5.17e-15
Kurtosis: 4.188 Cond. No. 1.59e+04
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.59e+04. This might indicate that there are
strong multicollinearity or other numerical problems.