4.3 스케일링#
이 절에서는 회귀분석에 있어 필수적인 스케일링의 목적과 방법에 대해 공부한다.
조건수#
보스턴 집값 데이터 예측문제를 statsmodels 패키지로 풀어 summary 리포트를 출력해보자.
from sklearn.datasets import load_boston
boston = load_boston()
dfX = pd.DataFrame(boston.data, columns=boston.feature_names)
dfy = pd.DataFrame(boston.target, columns=["MEDV"])
df = pd.concat([dfX, dfy], axis=1)
model1 = sm.OLS.from_formula("MEDV ~ " + "+".join(boston.feature_names), data=df)
result1 = model1.fit()
print(result1.summary())
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.741
Model: OLS Adj. R-squared: 0.734
Method: Least Squares F-statistic: 108.1
Date: Sun, 05 Jul 2020 Prob (F-statistic): 6.72e-135
Time: 13:20:08 Log-Likelihood: -1498.8
No. Observations: 506 AIC: 3026.
Df Residuals: 492 BIC: 3085.
Df Model: 13
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 36.4595 5.103 7.144 0.000 26.432 46.487
CRIM -0.1080 0.033 -3.287 0.001 -0.173 -0.043
ZN 0.0464 0.014 3.382 0.001 0.019 0.073
INDUS 0.0206 0.061 0.334 0.738 -0.100 0.141
CHAS 2.6867 0.862 3.118 0.002 0.994 4.380
NOX -17.7666 3.820 -4.651 0.000 -25.272 -10.262
RM 3.8099 0.418 9.116 0.000 2.989 4.631
AGE 0.0007 0.013 0.052 0.958 -0.025 0.027
DIS -1.4756 0.199 -7.398 0.000 -1.867 -1.084
RAD 0.3060 0.066 4.613 0.000 0.176 0.436
TAX -0.0123 0.004 -3.280 0.001 -0.020 -0.005
PTRATIO -0.9527 0.131 -7.283 0.000 -1.210 -0.696
B 0.0093 0.003 3.467 0.001 0.004 0.015
LSTAT -0.5248 0.051 -10.347 0.000 -0.624 -0.425
==============================================================================
Omnibus: 178.041 Durbin-Watson: 1.078
Prob(Omnibus): 0.000 Jarque-Bera (JB): 783.126
Skew: 1.521 Prob(JB): 8.84e-171
Kurtosis: 8.281 Cond. No. 1.51e+04
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.51e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
가장 하단에 다음과 같은 경고 메세지를 볼 수 있다.
[2] The condition number is large, 1.51e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
해석하면 다음과 같다.
조건수(conditiona number)가 15100으로 너무 큽니다.
강한 다중공선성(multicollinearity)이나 다른 수치적 문제가 있을 수 있습니다.
행렬의 조건수(conditional number)는 가장 큰 고유치와 가장 작은 고유치의 비율을 뜻한다. 회귀분석에서는 공분산행렬 \(X^TX\)의 가장 큰 고유치와 가장 작은 고유치의 비율이 된다.
여기에서는 다음 연립방정식을 예로 들어 설명을 하겠다.
이런 연립방정식이 있을 때 행렬 \(A\)의 조건수가 크면 계수행렬 \(A\)와 상수벡터 \(b\)에 대한 해 \(x\)의 민감도가 커지고 따라서 계수행렬이나 상수벡터에 존재하는 오차가 해에 미치는 영향이 커진다.
조건수는 가장 작은 경우의 예는 행렬 \(A\)가 단위 행렬인 경우다. 이 때 조건수의 값은 1이다.
A = np.eye(4)
이 행렬 \(A\)와 곱해져서 상수 벡터 \(b\)가 되는 벡터 \(x\)를 역행렬 \(A^{-1}\)을 사용하여 계산할 수 있다. 이 예에서는 상수 벡터 \(b\)가 1-벡터이다.
b = np.ones(4)
x = sp.linalg.solve(A, b)
x
array([1., 1., 1., 1.])
만약 상수 벡터에 약간의 오차가 있었다면 연립방정식의 해에도 동일한 수준의 오차가 발행한다. 다음 코드과 실행결과는 행렬 \(A\)에 1/10000 오차가 있으면 해 \(x\)에도 유사한 정도의 오차가 생기는 것을 보이고 있다.
x_error = sp.linalg.solve(A + 0.0001 * np.eye(4), b)
x_error
array([0.99990001, 0.99990001, 0.99990001, 0.99990001])
이번에는 다음과 같은 행렬을 생각하자.
A = sp.linalg.hilbert(4)
A
array([[1. , 0.5 , 0.33333333, 0.25 ],
[0.5 , 0.33333333, 0.25 , 0.2 ],
[0.33333333, 0.25 , 0.2 , 0.16666667],
[0.25 , 0.2 , 0.16666667, 0.14285714]])
이 행렬은 4차 힐버트 행렬(Hilbert matrix)이라는 행렬로 조건수가 15000이 넘는다.
np.linalg.cond(A)
15513.738738929038
이렇게 연립방정식을 이루는 행렬의 조건수가 커지면 상수항 오차가 작은 경우에도 해의 오차가 커지게 된다. 오차가 없는 경우의 해 \(x\)는 다음과 같다.
sp.linalg.solve(A, b)
array([ -4., 60., -180., 140.])
하지만 이 경우에는 계수행렬이나 상수벡터에 약간의 오차만 있어도 해가 전혀 다른 값을 가진다. 다음 코드는 계수행렬에 1/10000의 오차가 있을 때 해의 값이 전혀 달라지는 것을 보인다.
sp.linalg.solve(A + 0.0001 * np.eye(4), b)
array([ -0.58897672, 21.1225671 , -85.75912499, 78.45650825])
따라서 공분산행렬 \(X^TX\)의 조건수가 크면 회귀분석을 사용한 예측값도 오차가 커진다.
회귀분석과 조건수#
회귀분석에서 조건수가 커지는 경우는 크게 두 가지가 있다.
변수들의 단위 차이로 인해 숫자의 스케일이 크게 달라지는 경우. 이 경우에는 스케일링(scaling)으로 해결한다.
다중 공선성 즉, 상관관계가 큰 독립 변수들이 있는 경우, 이 경우에는 변수 선택이나 PCA를 사용한 차원 축소 등으로 해결한다.
이를 독립변수의 분포모양으로 설명하면 다음 그림과 같다.
%load_ext tikzmagic
%%tikz -p kotex,pgfplots -l arrows.meta,calc -s 2000,1200 -f png
\coordinate (leftbottom) at (0,0);
\coordinate (righttop) at (17,7);
\fill[white,use as bounding box] (leftbottom) rectangle (righttop);
\draw[help lines, white] (leftbottom) grid (righttop);
\tikzset{
>=stealth,font={\ttfamily\large}
}
\node at (4.5,6.5) {(1) 스케일링이 안된 경우};
\draw[->] (0.5,1) -- (8,1);
\draw[->] (1,0.5) -- (1,5);
\node at (8,0.7) {$x_1$};
\node at (0.7,5) {$x_2$};
\draw (4.5,3) circle (1cm and 0.1cm);
\draw (4.5,3) circle (2cm and 0.2cm);
\draw (4.5,3) circle (3cm and 0.3cm);
\draw (4.5,3) circle (4cm and 0.4cm);
\draw[->, line width=2pt] (4.5,3) -- (8,3);
\draw[->, line width=2pt] (4.5,3) -- (4.5,3.4);
\node at (8,3.5) {$\lambda_{max}$};
\node at (4.5,3.8) {$\lambda_{min}$};
\node at (12.5,6.5) {(2) 다중공선성이 있는 경우};
\draw[->] (8.5,1) -- (16,1);
\draw[->] (9,0.5) -- (9,5);
\node at (16,0.7) {$x_1$};
\node at (8.7,5) {$x_2$};
\begin{scope}[shift={(12.5,3)},rotate=30]
\draw (0,0) circle (1cm and 0.1cm);
\draw (0,0) circle (2cm and 0.2cm);
\draw (0,0) circle (3cm and 0.3cm);
\draw (0,0) circle (4cm and 0.4cm);
\draw[->, line width=2pt] (0,0) -- (3.5,0);
\draw[->, line width=2pt] (0,0) -- (0,0.4);
\end{scope}
\node at (15,5.2) {$\lambda_{max}$};
\node at (12,3.7) {$\lambda_{min}$};
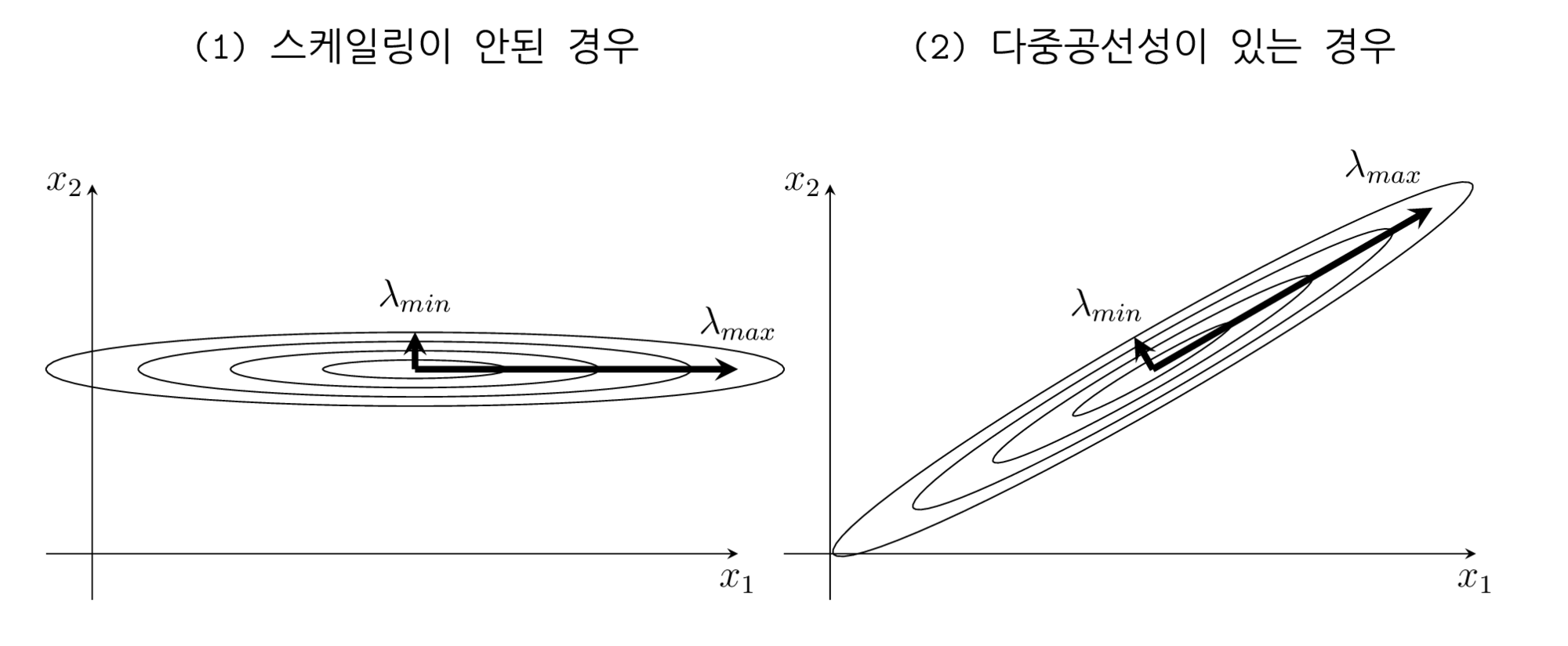
보스턴 집값 문제의 경우 각 독립변수들이 0.1 수준부터 100 수준까지 제각각의 크기를 가지고 있기 때문이다.
dfX.describe().loc["std"]
CRIM 8.601545
ZN 23.322453
INDUS 6.860353
CHAS 0.253994
NOX 0.115878
RM 0.702617
AGE 28.148861
DIS 2.105710
RAD 8.707259
TAX 168.537116
PTRATIO 2.164946
B 91.294864
LSTAT 7.141062
Name: std, dtype: float64
이렇게 독립변수가 스케일링 안되면 조건수가 커져서 예측 오차가 증폭될 가능성이 커진다. 이 효과를 확실하게 보기 위하여 일부러 다음처럼 TAX 변수를 크게 만들어 조건수를 증폭시켜 보았다.
dfX2 = dfX.copy()
dfX2["TAX"] *= 1e13
df2 = pd.concat([dfX2, dfy], axis=1)
model2 = sm.OLS.from_formula("MEDV ~ " + "+".join(boston.feature_names), data=df2)
result2 = model2.fit()
print(result2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.333
Model: OLS Adj. R-squared: 0.329
Method: Least Squares F-statistic: 83.39
Date: Sun, 05 Jul 2020 Prob (F-statistic): 8.62e-44
Time: 13:20:18 Log-Likelihood: -1737.9
No. Observations: 506 AIC: 3484.
Df Residuals: 502 BIC: 3501.
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.0038 0.000 -8.543 0.000 -0.005 -0.003
CRIM -0.1567 0.046 -3.376 0.001 -0.248 -0.066
ZN 0.1273 0.016 7.752 0.000 0.095 0.160
INDUS -0.1971 0.019 -10.433 0.000 -0.234 -0.160
CHAS 0.0034 0.000 12.430 0.000 0.003 0.004
NOX -0.0023 0.000 -9.285 0.000 -0.003 -0.002
RM 0.0267 0.002 14.132 0.000 0.023 0.030
AGE 0.1410 0.017 8.443 0.000 0.108 0.174
DIS -0.0286 0.004 -7.531 0.000 -0.036 -0.021
RAD 0.1094 0.018 6.163 0.000 0.075 0.144
TAX 1.077e-15 2.66e-16 4.051 0.000 5.55e-16 1.6e-15
PTRATIO -0.1124 0.011 -10.390 0.000 -0.134 -0.091
B 0.0516 0.003 19.916 0.000 0.046 0.057
LSTAT -0.6569 0.056 -11.790 0.000 -0.766 -0.547
==============================================================================
Omnibus: 39.447 Durbin-Watson: 0.863
Prob(Omnibus): 0.000 Jarque-Bera (JB): 46.611
Skew: 0.704 Prob(JB): 7.56e-11
Kurtosis: 3.479 Cond. No. 1.19e+17
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.19e+17. This might indicate that there are
strong multicollinearity or other numerical problems.
조건수가 1000조 수준으로 증가한 것을 볼 수 있다. R-squared로 표시되는 성능지표도 크게 감소하였다. 이 성능지표에 대해서는 추후 분산분석에서 자세히 다룬다.
statsmodels에서는 모형지정 문자열에서 scale() 명령을 사용하여 스케일링을 할 수 있다. 이 방식으로 스케일을 하면 스케일링에 사용된 평균과 표준편차를 저장하였다가 나중에 predict() 명령을 사용할 때도 같은 스케일을 사용하기 때문에 편리하다. 카테고리 더미변수인 CHAS는 스케일을 하지 않는다는 점에 주의한다.
feature_names = list(boston.feature_names)
feature_names.remove("CHAS")
feature_names = ["scale({})".format(name) for name in feature_names] + ["CHAS"]
model3 = sm.OLS.from_formula("MEDV ~ " + "+".join(feature_names), data=df2)
result3 = model3.fit()
print(result3.summary())
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.741
Model: OLS Adj. R-squared: 0.734
Method: Least Squares F-statistic: 108.1
Date: Sun, 05 Jul 2020 Prob (F-statistic): 6.72e-135
Time: 13:20:19 Log-Likelihood: -1498.8
No. Observations: 506 AIC: 3026.
Df Residuals: 492 BIC: 3085.
Df Model: 13
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept 22.3470 0.219 101.943 0.000 21.916 22.778
scale(CRIM) -0.9281 0.282 -3.287 0.001 -1.483 -0.373
scale(ZN) 1.0816 0.320 3.382 0.001 0.453 1.710
scale(INDUS) 0.1409 0.421 0.334 0.738 -0.687 0.969
scale(NOX) -2.0567 0.442 -4.651 0.000 -2.926 -1.188
scale(RM) 2.6742 0.293 9.116 0.000 2.098 3.251
scale(AGE) 0.0195 0.371 0.052 0.958 -0.710 0.749
scale(DIS) -3.1040 0.420 -7.398 0.000 -3.928 -2.280
scale(RAD) 2.6622 0.577 4.613 0.000 1.528 3.796
scale(TAX) -2.0768 0.633 -3.280 0.001 -3.321 -0.833
scale(PTRATIO) -2.0606 0.283 -7.283 0.000 -2.617 -1.505
scale(B) 0.8493 0.245 3.467 0.001 0.368 1.331
scale(LSTAT) -3.7436 0.362 -10.347 0.000 -4.454 -3.033
CHAS 2.6867 0.862 3.118 0.002 0.994 4.380
==============================================================================
Omnibus: 178.041 Durbin-Watson: 1.078
Prob(Omnibus): 0.000 Jarque-Bera (JB): 783.126
Skew: 1.521 Prob(JB): 8.84e-171
Kurtosis: 8.281 Cond. No. 10.6
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
스케일링만으로 조건수가 10.6이 된 것을 확인할 수 있다.