9.1 확률분포의 추정¶

‘분석하고자 하는 데이터가 어떤 확률변수로부터 실현된 표본이다’는 데이터 분석의 첫 번째 가정이다. 이 말은 우리가 정말 관심이 있는 것이 지금 손에 가지고 있는 데이터 즉, 하나의 실현체에 불과한 표본이 아니라 그 뒤에서 이 데이터를 만들어내는 확률변수의 분포라는 뜻이다. 확률론적인 관점에서 볼 때 데이터는 이 확률변수의 분포를 알아내기 위한 일련의 참고 자료일 뿐이다. 따라서 우리는 데이터 즉 표본으로부터 확률변수의 분포를 알아내야 한다.

확률분포의 결정¶

확률분포를 알아내는 일은 다음처럼 두 작업으로 나뉜다.

확률변수가 우리가 배운 베르누이분포, 이항분포, 정규분포 등의 기본 분포 중 어떤 확률분포를 따르는지 알아낸다.
데이터로부터 해당 확률분포의 모수의 값을 구한다.

첫 번째 작업 즉, 확률변수가 어떤 확률분포를 따르는가는 데이터가 생성되는 원리를 알거나 데이터의 특성을 알면 추측할 수 있다. 히스토그램을 그려서 확률분포의 모양을 살펴보고 힌트를 얻을 수도 있다.

데이터는 0 또는 1 뿐이다. \(\rightarrow\) 베르누이분포
데이터는 카테고리 값이어야 한다. \(\rightarrow\) 카테고리분포
데이터는 0과 1 사이의 실수 값이어야 한다. \(\rightarrow\) 베타분포
데이터는 항상 0 또는 양수이어야 한다. \(\rightarrow\) 로그정규분포, 감마분포, F분포, 카이제곱분포, 지수분포, 하프코시분포 등
데이터가 크기 제한이 없는 실수다. \(\rightarrow\) 정규분포 또는 스튜던트 t분포, 코시분포, 라플라스분포 등

이 규칙에는 예외가 있을 수 있다. 예를 들어 항상 양수인 데이터인 경우에도 정규분포로 모형화가 가능하다면 정규분포를 사용할 수 있다 정규분포와 스튜던트 t분포와 같이 둘 중 어느 것인지 구분하기 힘든 경우에는 뒤에서 설명할 정규성 검정이나 KS검정을 사용한다.

연습 문제 9.1.1¶

다음 코드로 사이킷런 패키지가 제공하는 보스턴 집값 데이터를 살펴보고 각각의 데이터의 확률분포 특성을 설명하라. 각 데이터에 적합한 확률분포가 존재한다면 어떤 확률분포인지도 설명하라.

from sklearn.datasets import load_boston
boston = load_boston()
dfX = pd.DataFrame(boston.data, columns=boston.feature_names)
dfy = pd.DataFrame(boston.target, columns=["MEDV"])
df = pd.concat([dfX, dfy], axis=1)

모수 추정 방법론¶

두번째 작업 즉, **모수의 값으로 가장 가능성이 높은 하나의 숫자를 찾아내는 작업을 모수 추정(parameter estimation)**이라고 한다. 모수 추정 방법에는 다음과 같은 방법들이 있다. 이 절에서는 우선 모멘트 방법을 공부한다. 최대가능도 추정법과 베이즈 추정법은 다음 절에서 공부한다.

모멘트 방법
최대가능도 추정법
베이즈 추정법

모멘트 방법¶

모멘트 방법(method of moment)은 표본자료에 대한 표본모멘트가 확률분포의 이론적 모멘트와 같다고 가정하여 모수를 구한다.

\[ \begin{align} \mu = \text{E}[X] \triangleq \bar{x} = \dfrac{1}{N} \sum_{i=1}^N x_i \tag{9.1.1} \end{align} \]

위 식에서 \(N\)은 데이터의 개수, \(x_i\)는 표본 데이터다.

2차 모멘트(분산)의 경우에는 다음과 같다.

\[ \begin{align} \sigma^2 = \text{E}[(X-\mu)^2] \triangleq \bar{s}^2 = \dfrac{1}{N-1} \sum_{i=1}^N (x_i - \bar{x})^2 \tag{9.1.2} \end{align} \]

예제: 베르누이분포의 모수 추정¶

모멘트 방법으로 베르누이 확률변수의 모수 \(\mu\)를 구하면 다음과 같다. 이 식에서 \(N_1\)은 1의 개수이다.

\[ \begin{align} \text{E}[X] = \mu \triangleq \bar{x} = \dfrac{1}{N} \sum_{i=1}^N x_i = \dfrac{N_1}{N} \tag{9.1.3} \end{align} \]

예제: 정규분포의 모수 추정¶

모멘트 방법으로 정규분포의 모수 \(\mu\), \(\sigma^2\)를 구하면 다음과 같다.

\[ \begin{align} \text{E}[X] = \mu \triangleq \bar{x} = \dfrac{1}{N} \sum_{i=1}^N x_i \tag{9.1.4} \end{align} \]

\[ \begin{align} \text{E}[(X-\mu)^2] = \sigma^2 \triangleq s^2 = \dfrac{1}{N-1} \sum_{i=1}^N (x_i - \bar{x})^2 \tag{9.1.5} \end{align} \]

정규분포는 모수가 아예 모멘트로 정의되어 있기 때문에 모멘트 방법을 사용하면 아주 쉽게 모수를 추정할 수 있다.

예제: 베타 분포의 모수 추정¶

모멘트 방법으로 베타 분포의 모수 \(a\), \(b\)를 구하면 다음과 같다. 이 경우에는 모수와 모멘트 간의 관계를 이용하여 비선형 연립 방정식을 풀어야 한다.

\[ \begin{align} \text{E}[X] = \dfrac{a}{a+b} \triangleq \bar{x} \tag{9.1.6} \end{align} \]

\[ \begin{align} \text{E}[(X-\mu)^2] = \dfrac{ab}{(a+b)^2(a+b+1)} \triangleq s^2 \tag{9.1.7} \end{align} \]

이 비선형 연립방정식을 풀어 해를 구하면 다음과 같다.

\[ \begin{align} a = \bar{x} \left( \frac{\bar{x} (1 - \bar{x})}{s^2} - 1 \right) \tag{9.1.8} \end{align} \]

\[ \begin{align} b = (1 - \bar{x}) \left( \frac{\bar{x} (1 - \bar{x})}{s^2} - 1 \right) \tag{9.1.9} \end{align} \]

예를 들어 다음과 같은 데이터 100개가 있다고 하자. 값이 항상 0과 1사이에 있으므로 베타분포를 따른다고 가정하다. 사실 이 데이터는 \(a=15, b=12\)인 베타분포에서 생성한 것이다.

np.random.seed(0)
x = sp.stats.beta(15, 12).rvs(10000)

sns.distplot(x, kde=False, norm_hist=True)
plt.title("베타 분포를 따르는 표본의 히스토그램")
plt.show()

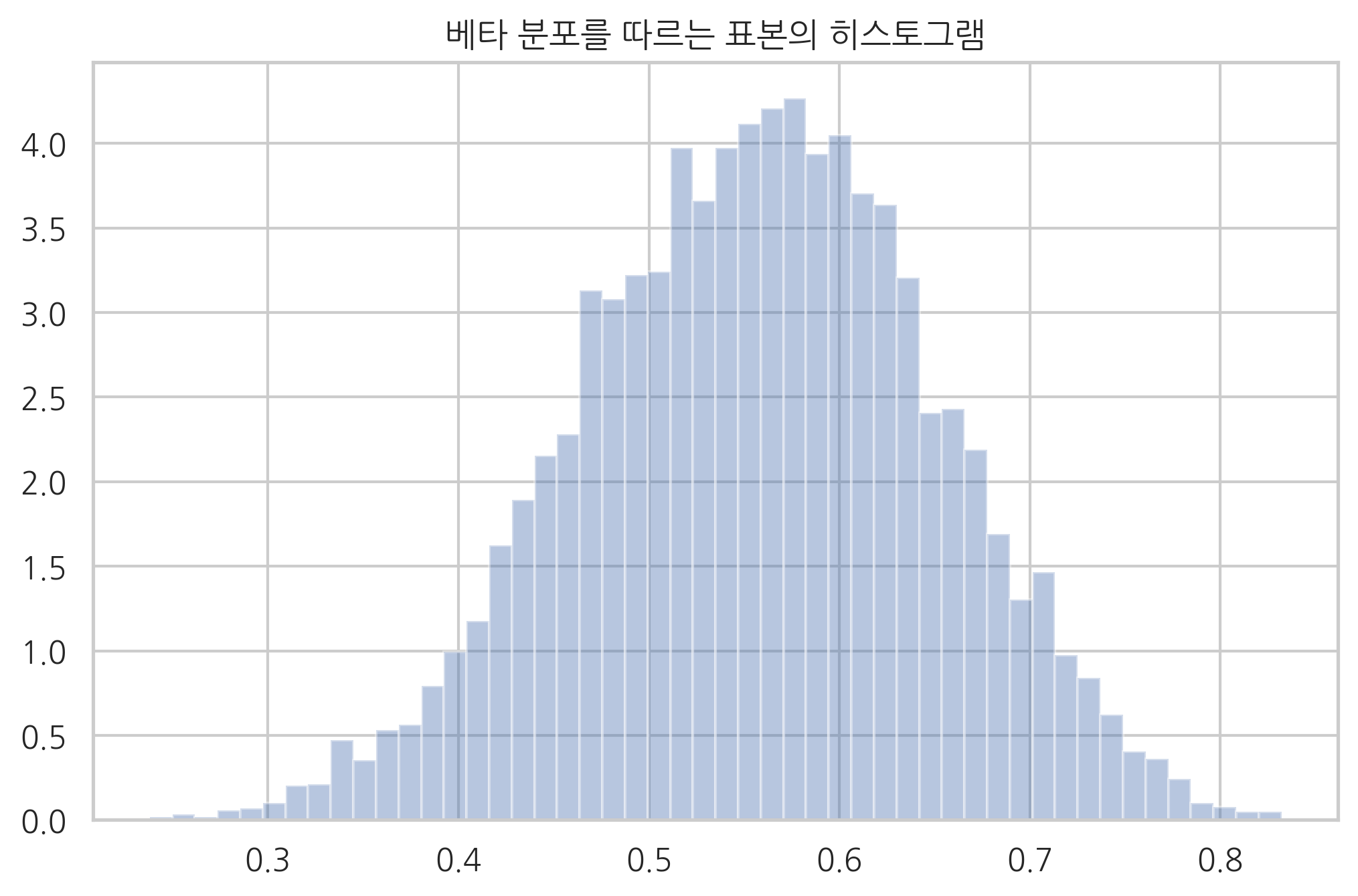
모멘트 방법으로 모수를 계산하면 원래의 모수와 비슷한 값을 구할 수 있다.

def estimate_beta(x):
    x_bar = x.mean()
    s2 = x.var()
    a = x_bar * (x_bar * (1 - x_bar) / s2 - 1)
    b = (1 - x_bar) * (x_bar * (1 - x_bar) / s2 - 1)
    return a, b


params = estimate_beta(x)
print(params)

(15.346682046700685, 12.2121537049535)

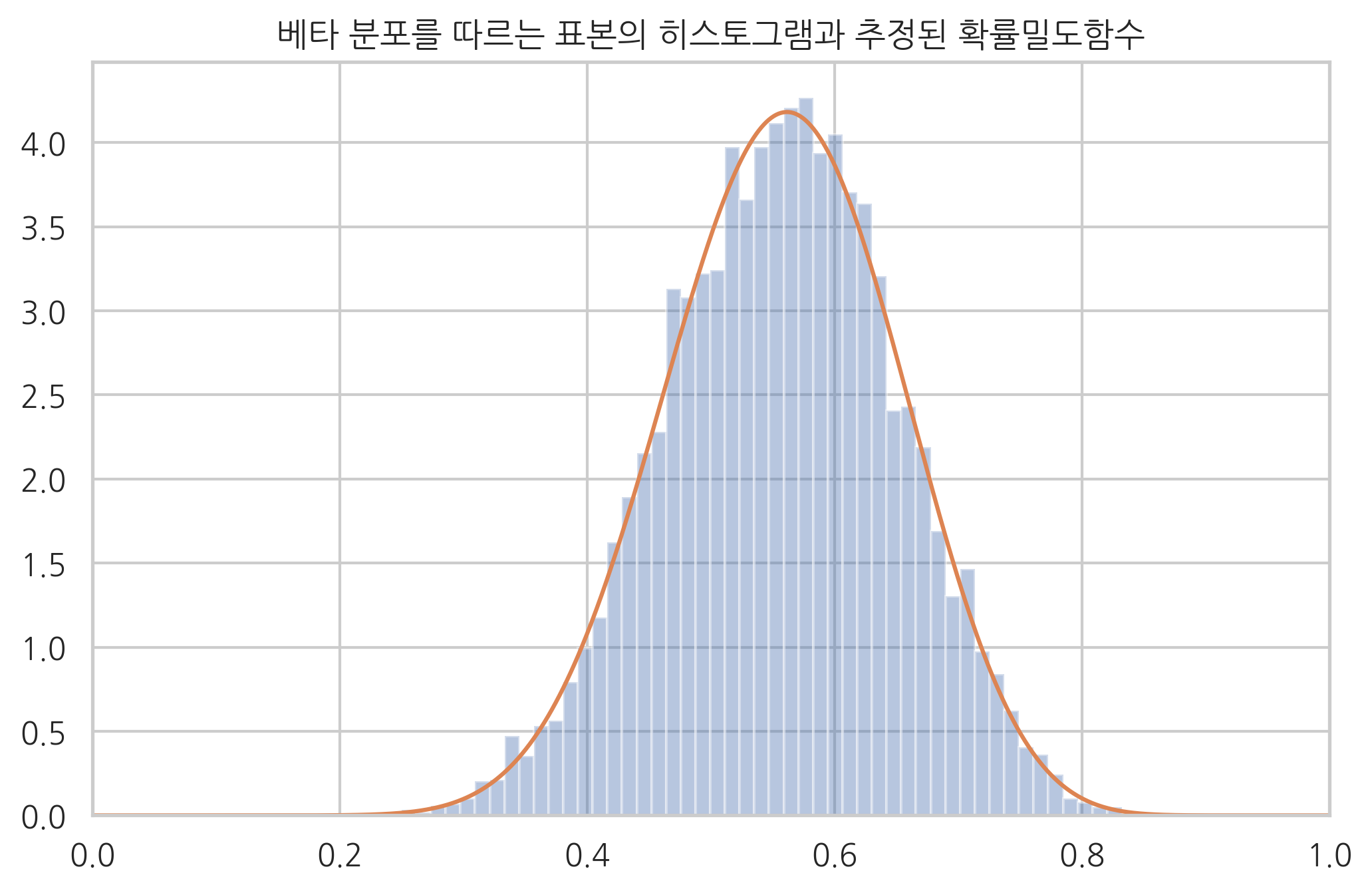
추정된 모수값으로 확률밀도분포를 그리면 히스토그램과 일치하는 것을 볼 수 있다.

xx = np.linspace(0, 1, 1000)
sns.distplot(x, kde=False, norm_hist=True)
plt.plot(xx, sp.stats.beta(params[0], params[1]).pdf(xx))
plt.xlim(0, 1)
plt.title("베타 분포를 따르는 표본의 히스토그램과 추정된 확률밀도함수")
plt.show()

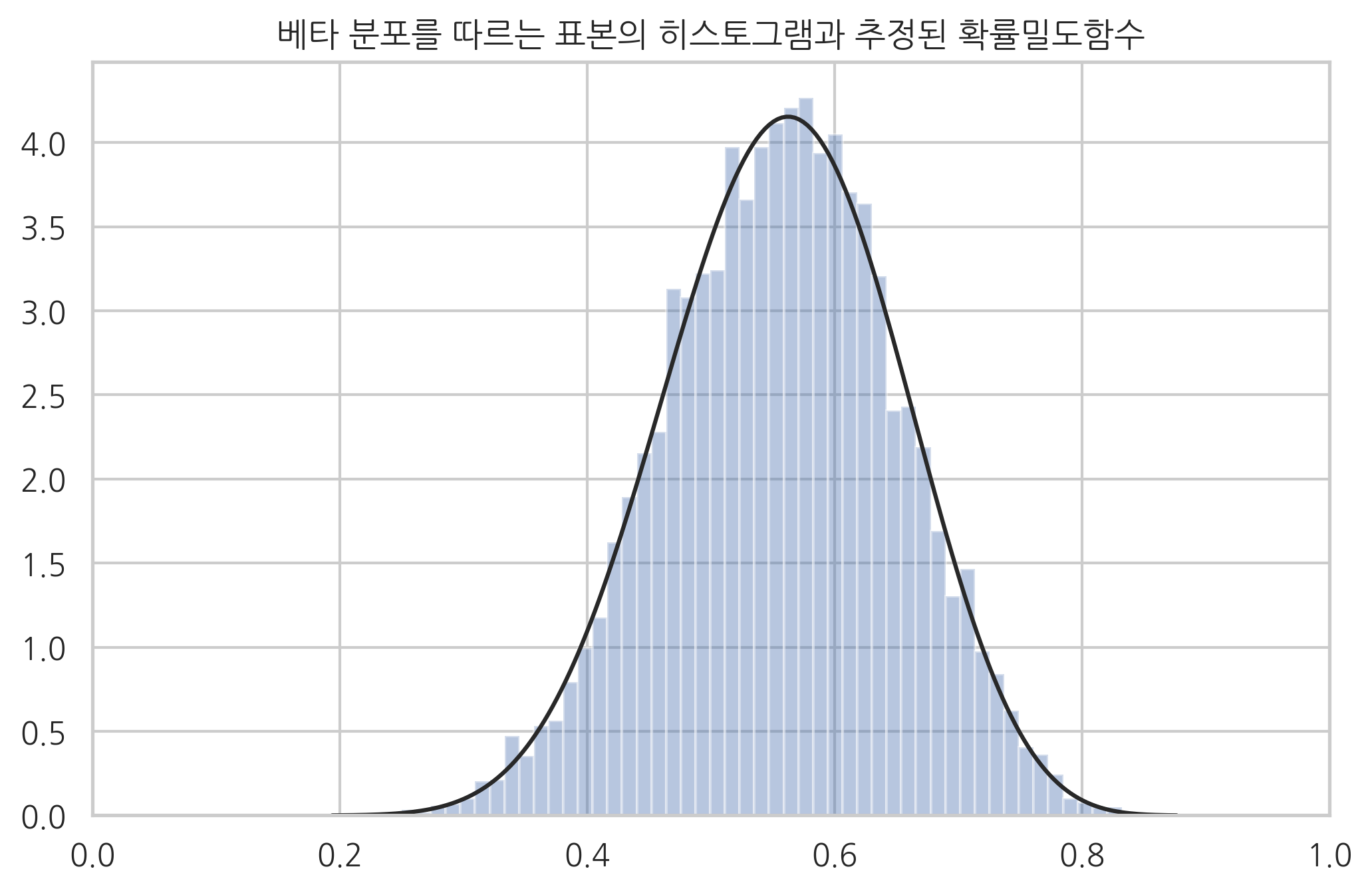
연속확률분포의 히스토그램을 그릴 수 있는 시본의 distplot() 함수에는 사실 모수 추정기능이 포함되어 있다. fit인수로 사이파이의 확률변수 명령을 넣으면 이 명령을 사용하여 모수를 추정한 뒤에 해당 확률밀도함수 그래프를 히스토그램과 함께 보여준다.

sns.distplot(x, kde=False, norm_hist=True, fit=sp.stats.beta)
plt.xlim(0, 1)
plt.title("베타 분포를 따르는 표본의 히스토그램과 추정된 확률밀도함수")
plt.show()

연습 문제 9.1.2¶

위 연습 문제에서 나온 보스턴 집값 데이터 각각에 대해 시본의 distplot() 함수로 히스토그램을 그려라. 그리고 distplot() 함수의 모수 추정 기능을 사용하여 각각의 데이터에 적합한 확률분포의 확률밀도함수를 그려라. (범주형 데이터는 제외한다.)

데이터 사이언스 스쿨