사운드 프로세싱 기초#
소리는 공기를 구성하는 입자들이 진동하는 현상이다. 공기의 진동을 측정하는 양적 기준을 음압(sound pressure)라고 한다. 사운드 데이터란 이 음압의 변화를 기록한 시계열 데이터이다.
사인 함수#
음압의 변화를 나타내는 시계열 데이터 중 가장 단순한 형태가 사인 함수(sine function)이다. 우선 사인 함수에 대해 알아보자. 삼각 함수 중 하나인 사인 함수는 다음과 같은 3가지 특징을 가진다.
진폭(amplitude) \(A\): 위 아래로 움직이는 폭. 소리의 크기로 인식된다.
주파수(frequency) \(\omega\) 또는 \(f\): 진동 속도. 주파수가 높으면 빠르게 진동한다. 소리의 높낮이로 인식된다.
위상(phase) \(\phi\): 사인 함수의 시작 시점. 위상 만큼 출발이 늦어진다. 위상의 차이는 소리의 시간차로 인식된다.
사인 함수를 수식으로 표현하면 다음과 같다.
또는
여기에서 \(t\)는 시간을 나타내며 보통은 초(second) 단위다.
주파수(frequency)는 초당 진동의 횟수를 나타낸다. 1회전의 각도가 \(360^{\circ} = 2\pi\) 라디안(radian)이므로 보통은 초당 라디안(radian per second) 단위로 표시하지만 이 값을 \(2\pi\)로 나누어 헤르쯔(Hz)라는 단위로 표시할 수도 있다. 1 Hz는 1초에 한 번 진동하는 주파수이다. 위 식에서 \(\omega\)는 초당 라디안 단위의 주파수이고 \(f\)는 헤르쯔 단위의 주파수이다.
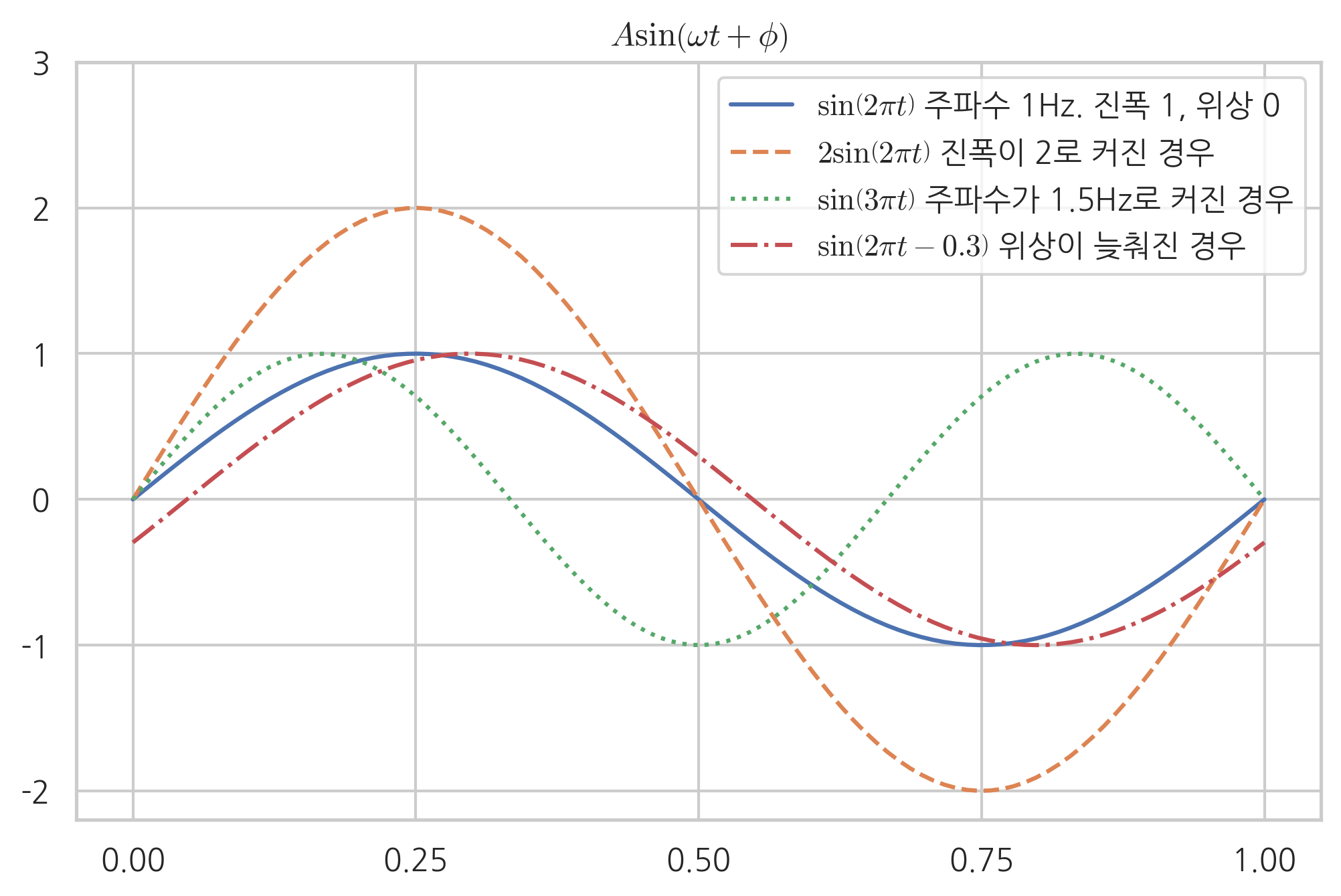
다음은 여러가지 사인 함수를 보여주는 코드이다. 이 코드에서 A는 진폭, w는 주파수 p는 위상을 나타낸다.
t = np.linspace(0, 1, 100)
plt.plot(t, 1 * np.sin(2 * np.pi * t + 0), ls="-", label=r"$\sin\left(2\pi{t}\right)$ 주파수 1Hz. 진폭 1, 위상 0")
plt.plot(t, 2 * np.sin(2 * np.pi * t + 0), ls="--", label=r"$2\sin\left(2\pi{t}\right)$ 진폭이 2로 커진 경우 ")
plt.plot(t, 1 * np.sin(3 * np.pi * t + 0), ls=":", label=r"$\sin\left(3\pi{t}\right)$ 주파수가 1.5Hz로 커진 경우")
plt.plot(t, 1 * np.sin(2 * np.pi * t - 0.3), ls="-.", label=r"$\sin\left(2\pi{t} - 0.3\right)$ 위상이 늦춰진 경우")
plt.ylim(-2.2, 3)
plt.xticks(np.linspace(0, 1, 5))
plt.legend()
plt.title(r"$A\sin\left(\omega{t}+\phi\right)$")
plt.show()
코사인 함수는 사인 함수와 위상이 90도 =\(\frac{\pi}{2}\) 라디안 차이가 있으므로 사인 함수의 일종으로 볼 수 있다.
주기와 주파수의 관계#
주파수 \(f\)의 역수를 주기 \(T\)라고 한다. 주기는 1번의 진동에 필요한 시간을 뜻한다.
또는
따라서 사인 함수는 다음처럼 쓸 수도 있다.
싱글 톤#
주파수는 사람에게 음의 높이(tone)로 인식된다. 사인파처럼 주파수가 일정한 음압 시계열은 사람에게 음높이가 일정한 “삐-“하는 기계음으로 들리기 때문에 하나의 사인파로 이루어진 소리를 싱글 톤(single tone)이라고도 한다. 전화를 걸 때 수신자가 전화를 받기 전까지 재생되는 통화연결음(ring tone)은 보통 400Hz~450Hz의 싱글 톤을 사용한다.
def single_tone(frequecy, sampling_rate=44100, duration=1):
# frequency: 주파수
# sampling_rate: 초당 샘플링 데이터 수. 디폴트 44100
# duration: 지속 시간. 단위 초. 디폴트 1초
t = np.linspace(0, duration, int(sampling_rate))
y = np.sin(2 * np.pi * frequecy * t)
return y
y = single_tone(400)
plt.plot(y[:400])
plt.show()
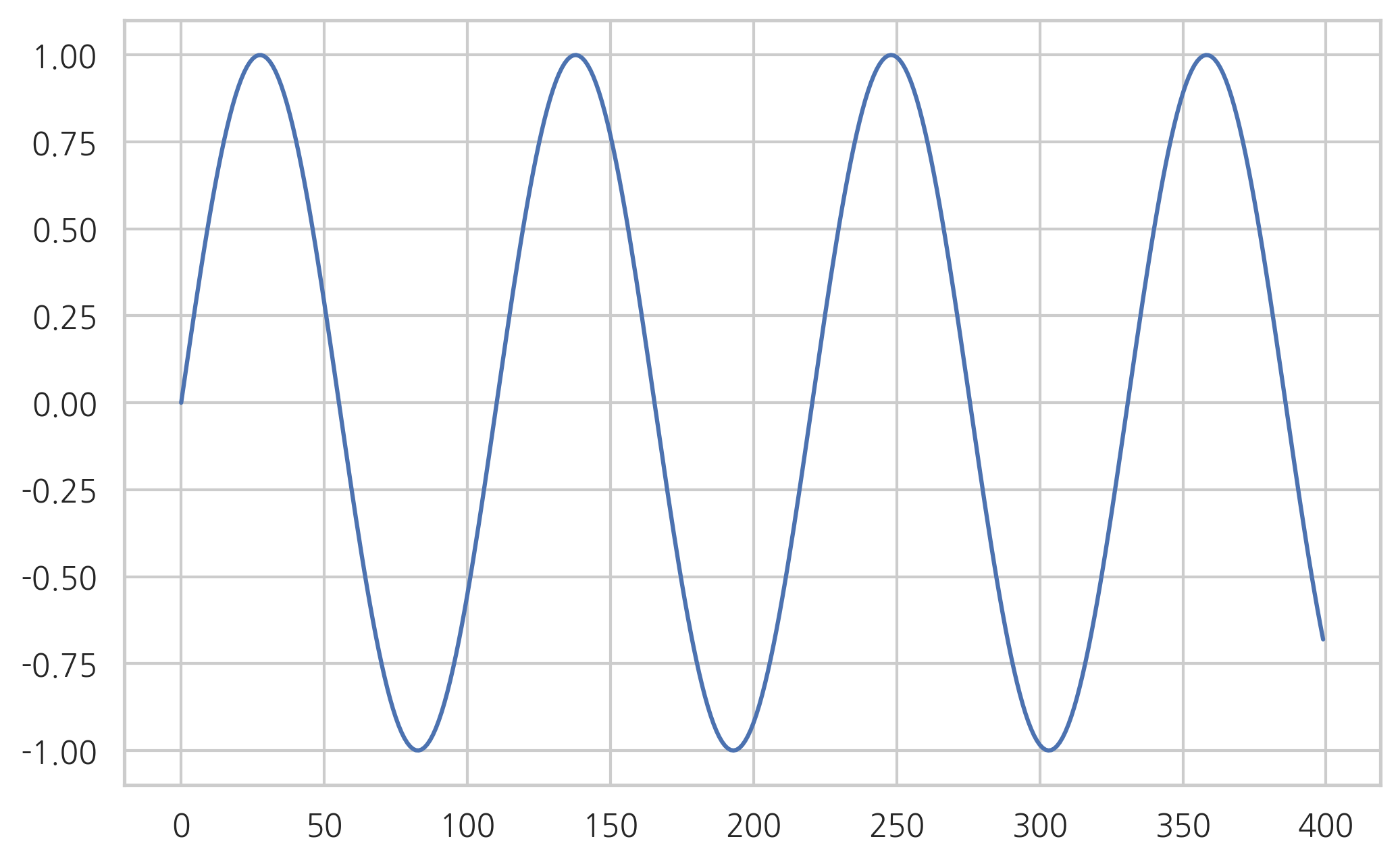
주피터 노트북에서는 다음 코드로 사운드 데이터를 표시할 수 있다.
from IPython.display import Audio, display
display(Audio(y, rate=44100))
음계에서 기준이 되는 가온다(middle C)음은 261.62Hz의 싱글 톤이다. 반음(semitone, half tone, half step)이 올라갈 때마다 \(2^{\frac{1}{12}}\)배만큼 주파수가 높아지고 12반음 즉, 1옥타브(octave)가 올라가면 주파수는 2배가 된다.
다음 코드는 가온다로부터 한 옥타브의 음에 대해 계산한 주파수이다.
notes = 'C,C#,D,D#,E,F,F#,G,G#,A,A#,B,C'.split(',')
freqs = 261.62 * 2**(np.arange(0, len(notes)) / 12.)
notes = list(zip(notes, freqs))
notes
[('C', 261.62),
('C#', 277.17673474627884),
('D', 293.6585210786982),
('D#', 311.1203654270119),
('E', 329.6205450734967),
('F', 349.2208026479644),
('F#', 369.98655218804913),
('G', 391.9870974524774),
('G#', 415.29586321592035),
('A', 439.9906403173536),
('A#', 466.1538452797511),
('B', 493.87279536756927),
('C', 523.24)]
octave = np.hstack([single_tone(f) for f in freqs])
display(Audio(octave, rate=44100))
복수의 싱글톤을 더하여 한번에 소리를 내면 화음이 된다. 예를 들어 도(C) 미(E) 솔(G) 3도 화음은 다음과 같다.
tone_C = single_tone(261.62)
tone_E = single_tone(329.62)
tone_G = single_tone(392)
harmony = tone_C + tone_E + tone_G
plt.plot(harmony[:10000])
plt.show()
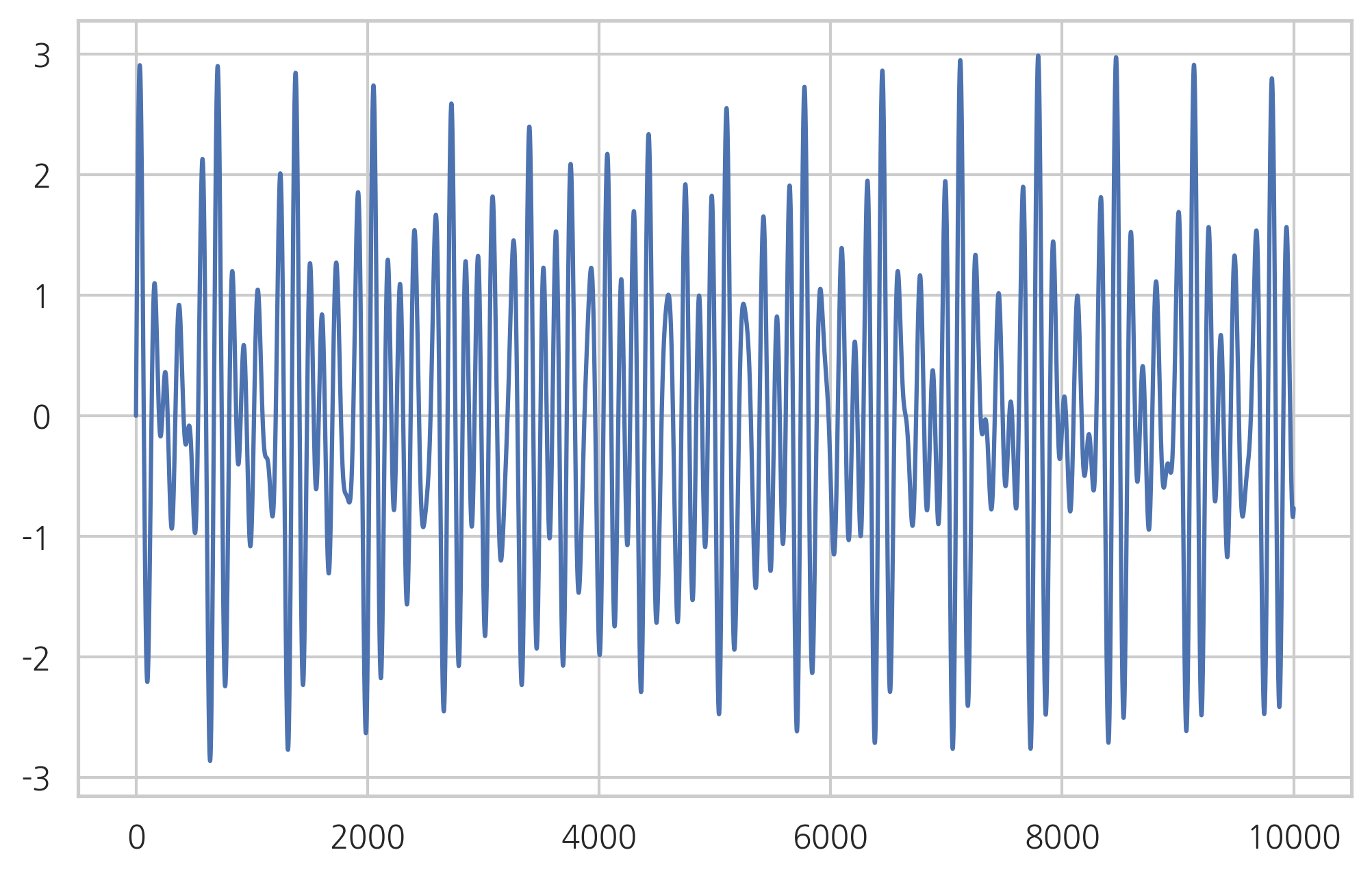
display(Audio(harmony, rate=44100))
wave 형식 파일#
wave 파일은 음압 시계열 데이터를 저장하는 가장 기본적인 파일 형식으로 .wav 확장자로 표시한다. wave 파일은 보통 초당 44100번 음압을 측정하고 \(-32768 \sim 32767(=2^{15})\)까지의 2바이트(bytes) 숫자로 기록한다.
파이썬에서 wave 파일을 쓰거나 읽기 위해서는 scipy 패키지의 io.wavfile 서브패키지에서 제공하는 read, write 명령을 사용한다.
import scipy.io.wavfile
# 초당 샘플링 데이터 수
sampling_rate = 44100
sp.io.wavfile.write("octave.wav", sampling_rate, octave)
sr, y_read = sp.io.wavfile.read("octave.wav")
# sr == sampling_rate
plt.plot(y_read[40000:50000])
plt.show()
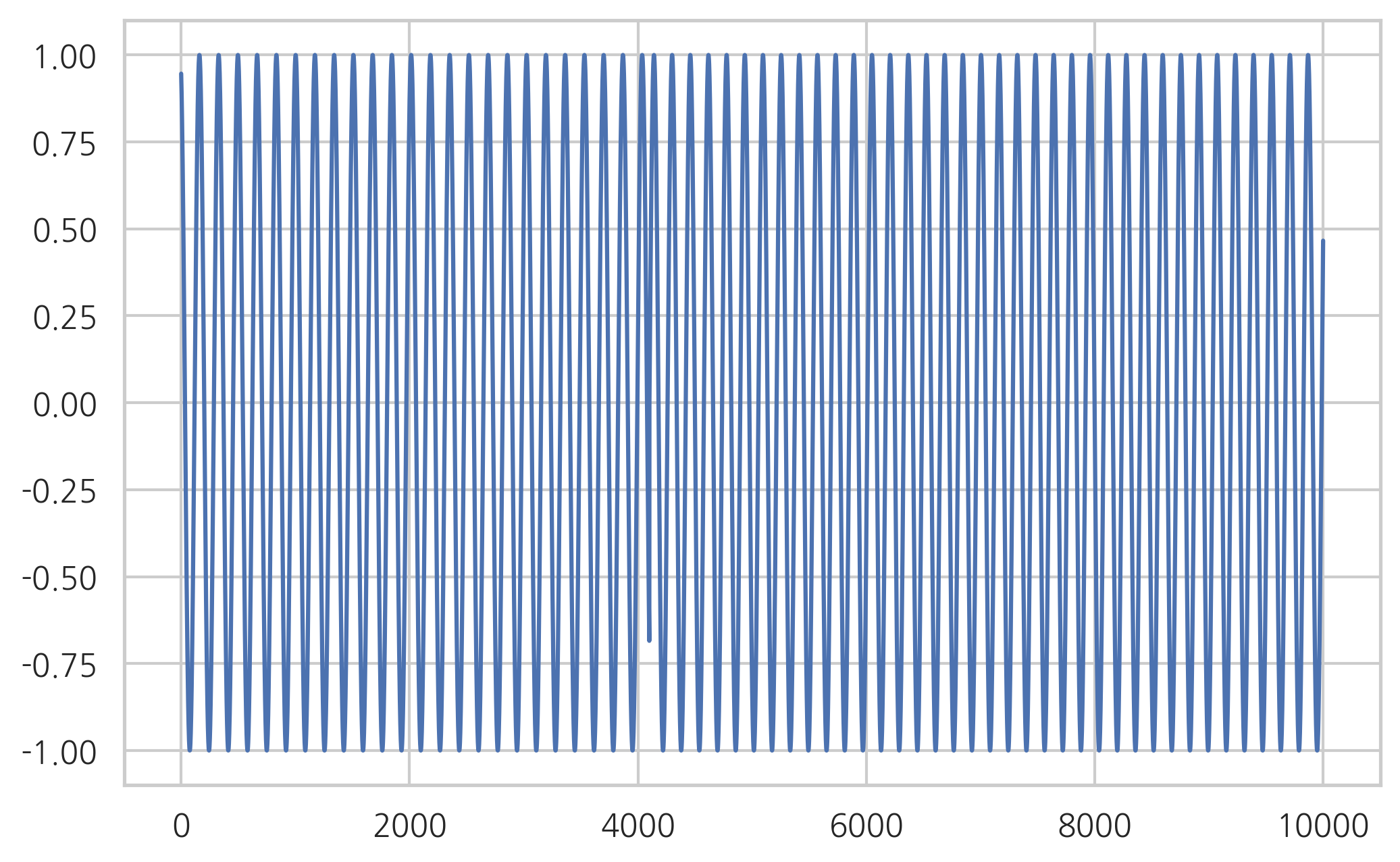
Audio(y_read, rate=sr)
Dual-tone multi-frequency signaling#
전화는 DTMF(Dual-tone multi-frequency) 방식이라는 두 싱글톤 조합의 음향 신호로 전화번호를 입력받는다.
| 1209 Hz | 1336 Hz | 1477 Hz | 1633 Hz | |
|---|---|---|---|---|
| 697 Hz | 1 | 2 | 3 | A |
| 770 Hz | 4 | 5 | 6 | B |
| 852 Hz | 7 | 8 | 9 | C |
| 941 Hz | * | 0 | # | D |
연습 문제 1#
DTMF를 사용하여 자신의 전화번호를 호출하는 음향 신호를 생성하라.