히든 마코프 모형¶

독립 혼합 모형(Independent Mixuture Model)¶

독립 혼합 모형(Independent Mixuture Model)은 연속 확률 변수이지만 단일한 확률 분포를 가지지 않고 복수의 연속 확률 분포 중 하나를 확률적으로 선택하는 모형을 말한다. 이 때 연속 확률 분포의 선택은 독립적인 이산 확률분포를 사용한다.

\[\begin{split} \begin{eqnarray*} p(x) &=& \sum_{i=1}^m {P}(C=i)\cdot {P}(X=x|C=i) \\ &=& \sum_{i=1}^m \delta_i p_i(x) \end{eqnarray*} \end{split}\]

\(p(x)\) : 전체 Independent Mixuture 분포
\(p_i(x)\) : Independent Mixuture의 각 성분(component)이 되는 개별적인 연속 확률분포
\(\delta_i\) : mixing parameter. 특정시간에 대해 모든 성분 중 특정한 \(p_i(x)\)가 선택될 확률. 이산 확률 분포
\(\sum\delta_i = 1\) : mixing parameter에 대한 확률 제한 조건

독립 혼합 모형의 예: 베르누이-정규 혼합 모형¶

베르누이-정규 혼합 모형(Bernoulli Normal-Mixuture Model)은 베르누이 확률 변수의 값에 따라 두 개의 서로 다른 연속 정규 분포 중 하나를 선택하는 확률 분포이다.

마코프 체인(Markov Chain)¶

마코프 체인은 다음과 같은 마코프(Markov) 특성을 가지는 이산시간 확률 프로세스를 말한다.

\[ P(C_{t+1} \mid C_t, \cdots, C_1) = P(C_{t+1} \mid C_t) \]

이 때 특정 시간 \(t\) 동안 특정한 한 상태 \(i\) 에서 특정한 다른 상태 \(j\) 로 전이할 확률을 ** 전이 확률(Transition Probability)** 이라고 한다.

\[ \gamma_{ij}(t) = P(C_{s+t}=j|C_{s}=i) \]

또한 모든 상태 조합에 대한 전이 확률을 나타낸 것이 전이 확률 행렬(Transition Probability Matirx)이다.

\[ \Gamma(t) = \{ \gamma_{ij}(t) \}, \;\;\; \Gamma = \Gamma(1) \]

체프먼-콜모고로프 방정식(Chapman-Kolmogorov Equation에 의하면 시간 \(t+u\) 의 전이확률행렬은 시간 \(t\) 의 전이확률행렬과 시간 \(u\) 의 전이확률행렬의 곱으로 나타난다.

\[ \Gamma(t+u) = \Gamma(t)\Gamma(u) \]

히든 마코프 모형(Hidden Markov Model)¶

히든 마코프 모형(Hidden Markov Model)은 독립 혼합 모형에서 연속 확률 분포를 선택하는 이산 확률 과정 \(C_t\)가 마코프 체인이고 연속 확률 분포\(X_t\) 가 그 시점의 이산 확률 과정의 값에만 의존하는 모형을 말한다. 그러나 연속 확률 분포의 값 \(X_t\) 만 측정 가능하고 이산 확률 과정의 값 \(C_t\) 는 측정할 수 없다.

\[ P(C_t \mid |C_{t-1}, \cdots, C_1) = P(C_t \mid C_{t-1}) \]

\[ P(X_t \mid X_t, \cdots, X_1, C_t, \cdots, C_1) = P(X_t \mid C_t) \]

hmmlearn 패키지¶

Python에는 다양한 HMM 시뮬레이션 및 추정용 패키지가 제공된다. 여기에서는 그 중 하나인 hmmlearn 패키지를 사용해보자.

hmmlearn의 hmm 서브 패키지에서는 다음과 같은 세가지 HMM 모형 클래스를 제공한다.

GaussianHMM
Hidden Markov Model with Gaussian emissions.
GMMHMM
Hidden Markov Model with Gaussian mixture emissions.
MultinomialHMM
Hidden Markov Model with multinomial (discrete) emissions

GaussianHMM 클래스를 사용하면 카테고리-다변수 정규분포 혼합 모형을 시뮬레이션 할 수 있다.

이 때 다음과 같은 속성을 설정할 수 있다.

startprob_: 초기 확률 벡터
transmat_: 전이 확률 행렬
means_: 정규 분포의 기댓값 벡터
covars_: 정규 분포의 공분산 행렬

가장 간단한 베르누이-정규 분포를 시험해보자.

from hmmlearn import hmm
np.random.seed(3)

model = hmm.GaussianHMM(n_components=2, covariance_type="diag")
model.startprob_ = np.array([0.9, 0.1])
model.transmat_ = np.array([[0.95, 0.05], [0.15, 0.85]])
model.means_ = np.array([[1.0], [-3.0]])
model.covars_ = np.array([[15.0], [40.0]])
X, Z = model.sample(500)

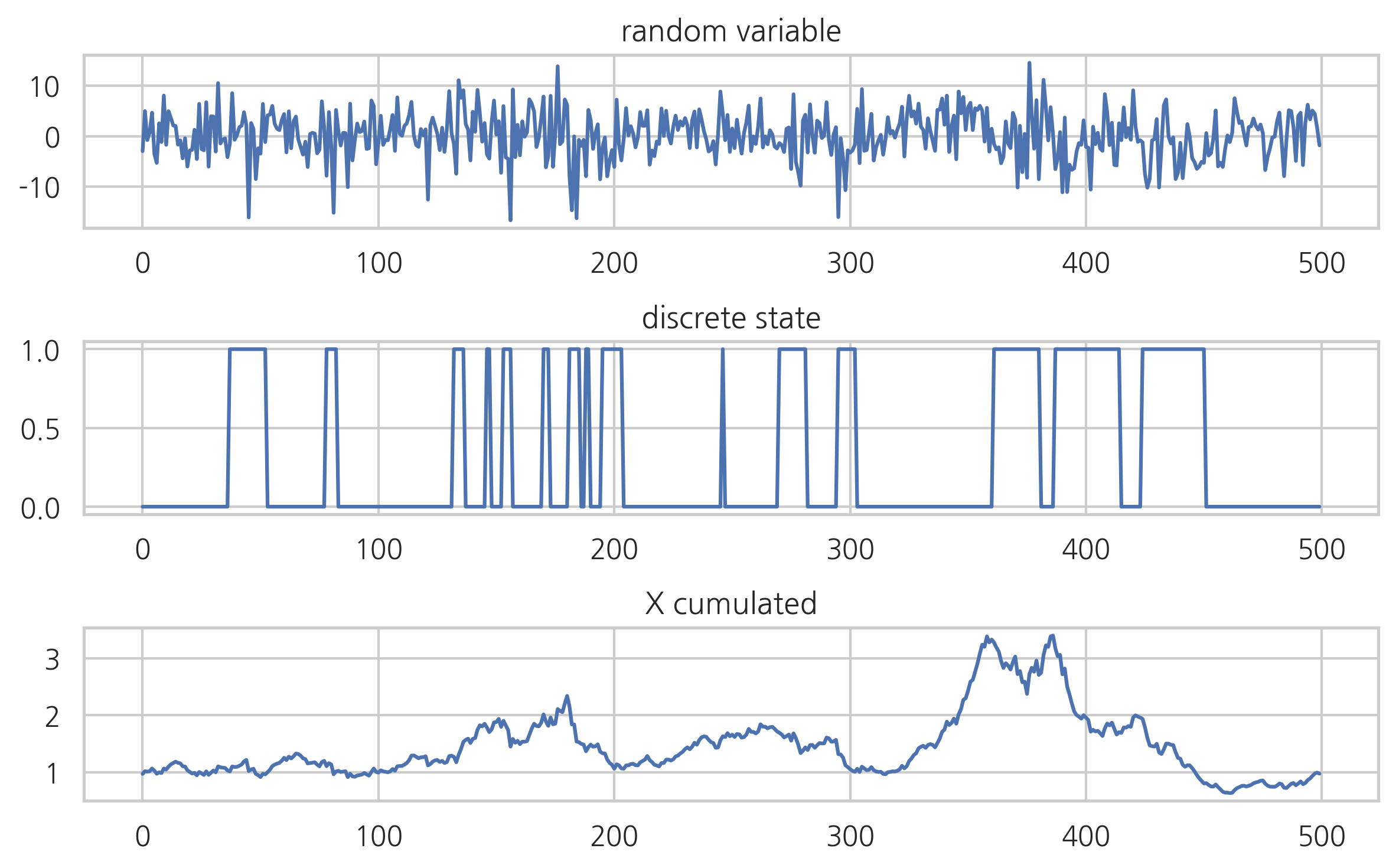
plt.subplot(311)
plt.plot(X)
plt.title("random variable")
plt.subplot(312)
plt.plot(Z)
plt.title("discrete state")
plt.subplot(313)
plt.plot((1 + 0.01*X).cumprod())
plt.title("X cumulated")
plt.tight_layout()
plt.show()

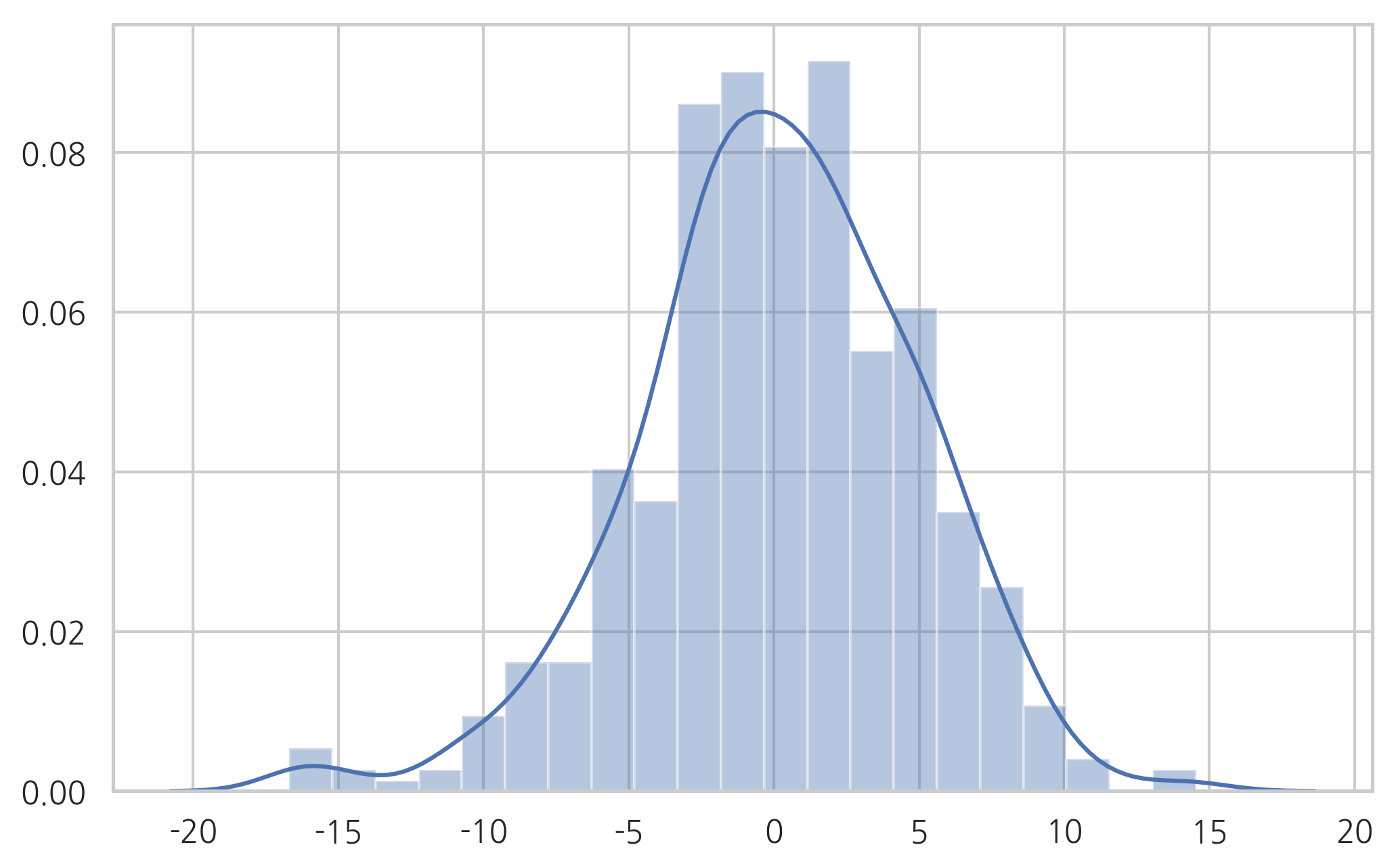
sns.distplot(X)
plt.show()

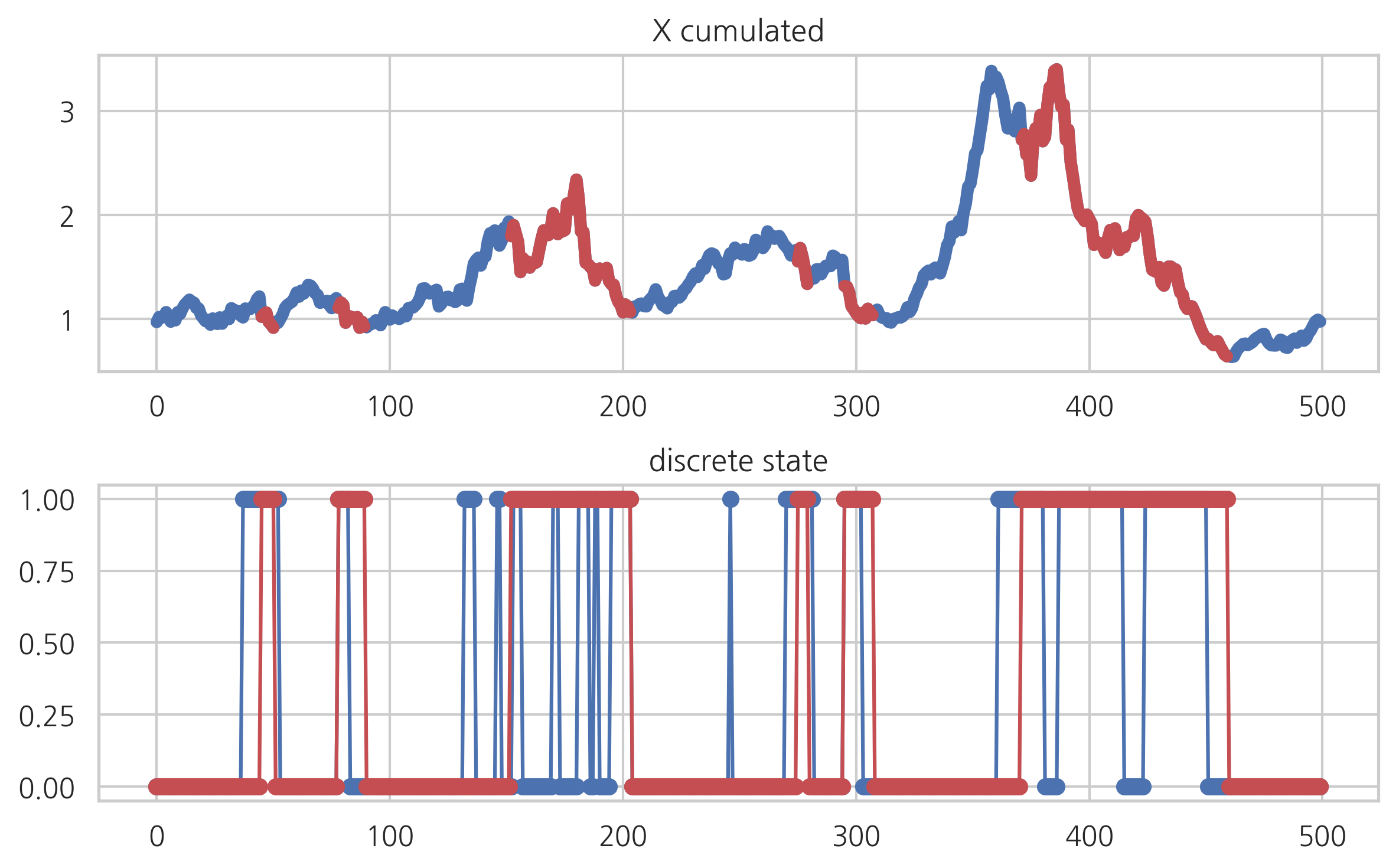
디코드¶

관측된 히든 마코프 모형의 연속 확률 변수 값으로부터 내부의 이산 확률 변수 값을 추정하는 과정을 디코드(decode)라고 한다. 디코드 알고리즘 중 가장 많이 사용되는 것은 Viterbi 알고리즘이다.

hmmlearn 패키지의 HMM 클래스들은 모형 추정을 위한 fit 메서드와 디코딩을 위한 decode 메서드를 제공한다. 다음은 위에서 시뮬레이션한 결과를 디코딩한 예이다.

model2 = hmm.GaussianHMM(n_components=2, n_iter=len(X)).fit(X)
model2

GaussianHMM(algorithm='viterbi', covariance_type='diag', covars_prior=0.01,
            covars_weight=1, init_params='stmc', means_prior=0, means_weight=0,
            min_covar=0.001, n_components=2, n_iter=500, params='stmc',
            random_state=None, startprob_prior=1.0, tol=0.01,
            transmat_prior=1.0, verbose=False)

Z_hat = model2.decode(X)[1]
X_cum = (1 + 0.01*X).cumprod()
X_cum_hat = X_cum.copy()
X_cum_hat[Z_hat == 0] = np.nan

plt.subplot(211)
plt.plot(X_cum, lw=5)
plt.plot(X_cum_hat, 'r-', lw=5)
plt.title("X cumulated")
plt.subplot(212)
plt.plot(Z, 'bo-')
plt.plot(Z_hat, 'ro-')
plt.title("discrete state")
plt.tight_layout()
plt.show()