7.4 다변수 확률변수¶

카테고리 값을 가질 수 있는 이산확률변수가 두 개 이상 있는 경우에는 각각의 확률변수에 대한 확률분포 이외에도 확률분포 쌍이 가지는 복합적인 확률분포를 살펴보아야 한다. 이 절에서는 이러한 다변수 확률변수의 확률분포를 표현하기 위한 결합확률분포함수를 알아본다. 두 확률변수 값의 쌍이 어떤 확률분포를 가지는지 안다면 둘 중 하나의 확률분포의 값을 알고 있을 때 다른 확률분포가 어떻게 되는지도 알 수 있다. 이러한 정보를 나타내는 것인 조건부확률분포에 대해서도 공부한다.

결합확률질량함수¶

주사위처럼 1부터 6까지의 값을 가지는 카테고리 분포 확률변수 \(X\)와 \(Y\)를 생각하자. 확률변수 각각의 확률적 특성은 확률질량함수 \( p_X(x), p_Y(y) \)로 나타낼 수 있다. 확률변수가 여러 개 있을 때는 확률질량함수의 아랫 첨자로 확률변수 이름을 지정하여 어떤 확률변수의 확률질량함수인지 표시한다. 만약 공정한 주사위처럼 모든 값이 나올 확률이 같다면 각각의 확률질량함수는 다음과 같을 것이다.

\[ \begin{align} p_X(1) = \dfrac{1}{6}, \ldots p_X(6) = \dfrac{1}{6} \tag{7.4.1} \end{align} \]

\[ \begin{align} p_Y(1) = \dfrac{1}{6}, \ldots p_Y(6) = \dfrac{1}{6} \tag{7.4.2} \end{align} \]

이번에는 하나의 값이 아닌 두 개의 값, 즉 특정한 숫자 쌍이 나타나는 경우를 생각하자. 단변수 이산확률변수와 같이 단순사건에 대한 확률만 알고 있으면 임의의 숫자 쌍 집합 즉, 임의의 사건에 대해서도 확률을 계산할 수 있으므로 하나 하나의 숫자 쌍에 대해 확률을 알려주는 확률질량함수만 있으면 전체 확률분포를 알 수 있다. 이러한 확률질량함수를 **결합확률질량함수(joint probability mass function)**이라고 하며 다음과 같이 표시한다.

\[ \begin{align} p_{XY}(x, y) \tag{7.4.3} \end{align} \]

이 때는 나타날 수 있는 숫자가 두 숫자로 이루어진 쌍이므로 독립변수가 \(x,y\) 두 개가 된다. 종속변수는 그 숫자 쌍이 나타날 확률이다. 즉, \(p_{XY}(2, 3)\)은 \(\{x=2, y=3\}\)이라는 특정한 숫자 쌍으로만 이루어진 사건의 확률이다. 만약 공정한 주사위 두 개를 던지는 경우라면 결합확률질량함수는 다음과 같을 것이다.

\[ \begin{align} p_{XY}(1,1) = \dfrac{1}{36}, p_{XY}(1,2) = \dfrac{1}{36}, \ldots, p_{XY}(6,6) = \dfrac{1}{36} \tag{7.4.4} \end{align} \]

예제¶

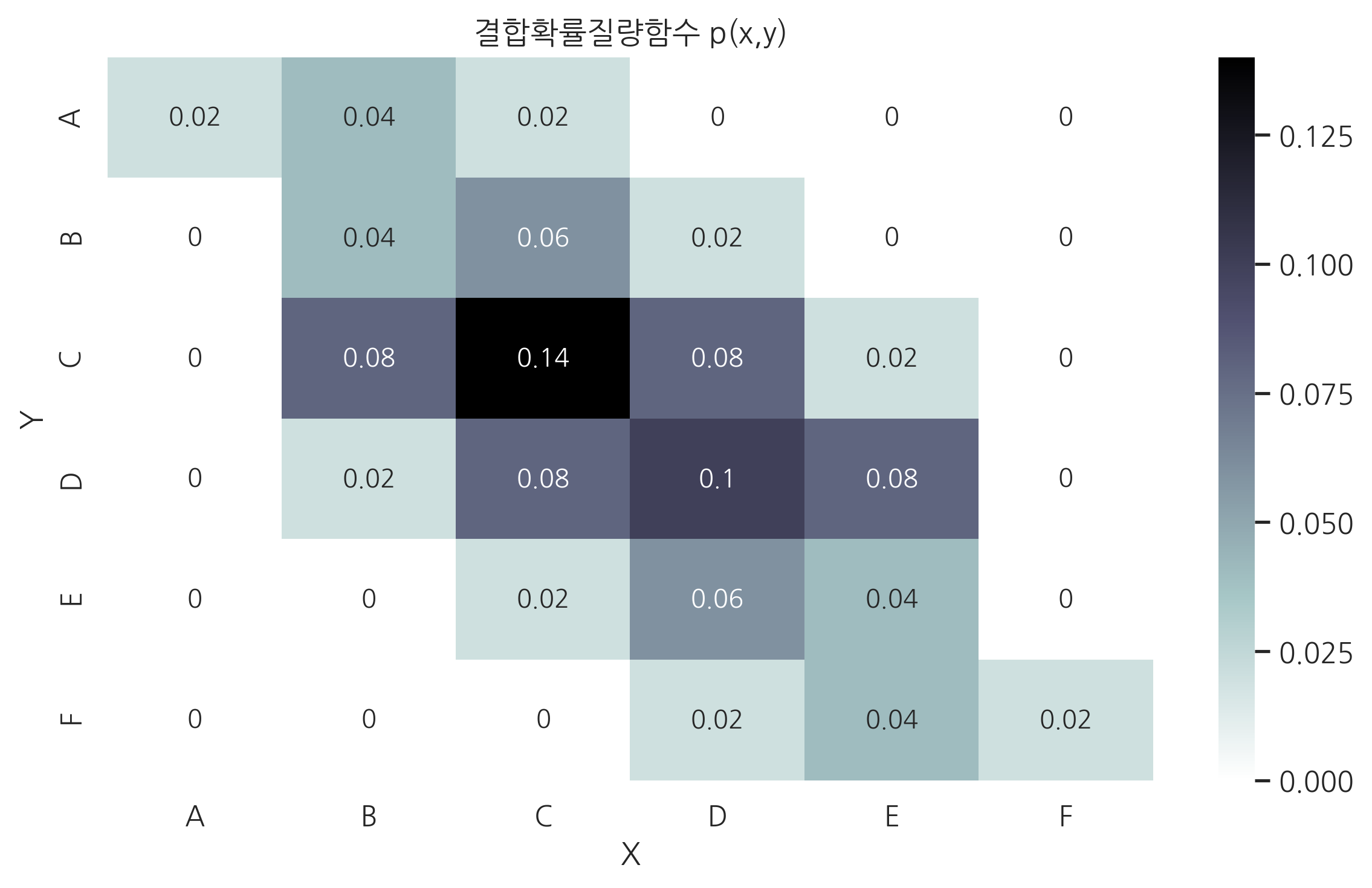
어느 대학교에서 50명의 학생이 X, Y 두 과목에 대해 시험을 보고 그 결과가 다음과 같이 A, B, C, D, E, F 학점으로 나왔다고 가정하자. 각 열은 X과목의 학점, 각 행은 Y과목의 학점을 나타내고 행렬의 숫자는 해당 학점 조합을 받은 학생의 수다. 예를 들어 X과목을 B학점, Y과목을 C학점 받은 학생은 4명이다.

grades = ["A", "B", "C", "D", "E", "F"]
scores = pd.DataFrame(
    [[1, 2, 1, 0, 0, 0],
     [0, 2, 3, 1, 0, 0],
     [0, 4, 7, 4, 1, 0],
     [0, 1, 4, 5, 4, 0],
     [0, 0, 1, 3, 2, 0],
     [0, 0, 0, 1, 2, 1]], 
    columns=grades, index=grades)
scores.index.name = "Y"
scores.columns.name = "X"
scores

X	A	B	C	D	E	F
Y
A	1	2	1	0	0	0
B	0	2	3	1	0	0
C	0	4	7	4	1	0
D	0	1	4	5	4	0
E	0	0	1	3	2	0
F	0	0	0	1	2	1

결합확률질량함수는 다음과 같다.

pmf = scores / scores.values.sum()
pmf

X	A	B	C	D	E	F
Y
A	0.02	0.04	0.02	0.00	0.00	0.00
B	0.00	0.04	0.06	0.02	0.00	0.00
C	0.00	0.08	0.14	0.08	0.02	0.00
D	0.00	0.02	0.08	0.10	0.08	0.00
E	0.00	0.00	0.02	0.06	0.04	0.00
F	0.00	0.00	0.00	0.02	0.04	0.02

이 확률질량함수를 히트맵(heat map)으로 나타내면 다음과 같다.

sns.heatmap(pmf, cmap=mpl.cm.bone_r, annot=True,
            xticklabels=['A', 'B', 'C', 'D', 'E', 'F'],
            yticklabels=['A', 'B', 'C', 'D', 'E', 'F'])
plt.title("결합확률질량함수 p(x,y)")
plt.tight_layout()
plt.show()

연습 문제 7.4.1¶

위에서 구한 데이터를 기준으로 다음 질문에 답하라.

이 확률변수의 표본 값이 (D,F)일 확률을 구하라.
이 확률변수의 표본 값이 (F,A)일 확률을 구하라.
확률변수의 값을 모른다고 할 때 어떤 값이 나올 가능성이 가장 높은가.

주변확률질량함수¶

**주변확률질량함수(marginal probability mass function)**는 두 확률변수 중 하나의 확률변수 값에 대해서만 확률분포를 표시한 함수이다. 즉 다변수가 되기 이전의 단변수 확률질량함수를 말한다.

결합확률질량함수에서 주변확률질량함수를 구하려면 전체 확률의 법칙에 의해 다른 변수가 가질 수 있는 모든 값의 결합확률질량함수를 합한 확률이 된다.

\[ \begin{align} p_X(x) = \sum_{y_i} p_{XY}(x,y_i) \tag{7.4.5} \end{align} \]

\[ \begin{align} p_Y(y) = \sum_{x_i} p_{XY}(x_i,y) \tag{7.4.6} \end{align} \]

위에서 예로 든 이산 확률변수의 경우에 과목 X만 관심이 있다면 결합확률질량함수 \(p_{XY}(x, y)\)로부터 X에 대한 주변확률질량함수 \(p_X(x)\)를 구해야 한다.

주변확률질량함수를 계산한 값은 다음과 같다.

\[\begin{split} \begin{align} \begin{aligned} p_X(A) &= p_{XY}(A,A) + p_{XY}(A,B) + p_{XY}(A,C) \\ &+ p_{XY}(A,D) + p_{XY}(A,E) + p_{XY}(A,F) \\ &= 0.02 \end{aligned} \tag{7.4.7} \end{align} \end{split}\]

pmf_marginal_x = pmf.sum(axis=0)
pmf_marginal_x

X
A    0.02
B    0.18
C    0.32
D    0.28
E    0.18
F    0.02
dtype: float64

pmf_marginal_y = pmf.sum(axis=1)
pmf_marginal_y[:, np.newaxis]

array([[0.08],
       [0.12],
       [0.32],
       [0.28],
       [0.12],
       [0.08]])

연습 문제 7.4.2¶

위에서 구한 데이터를 기준으로 다음 질문에 답하라.

확률변수 \(Y\)의 표본 값이 A일 확률을 구하라.
확률변수 \(X\)의 표본 값이 B일 확률을 구하라.

조건부확률질량함수¶

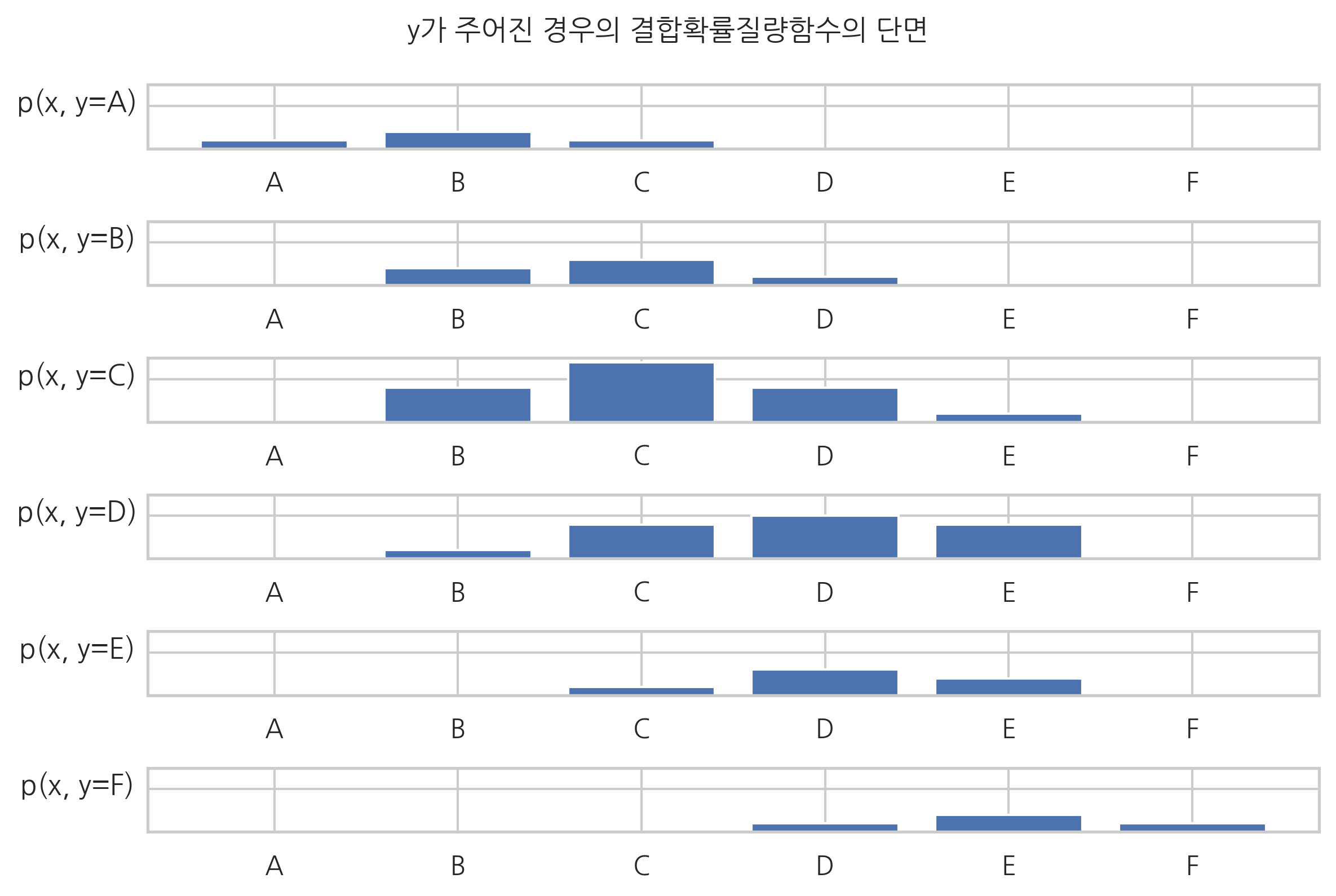
만약 \(y\)값이 특정한 값으로 고정되었다면 확률질량함수의 단면을 이용하여 다음과 같이 그릴 수도 있다.

import string

x = np.arange(6)
for i, y in enumerate(string.ascii_uppercase[:6]):
    ax = plt.subplot(6, 1, i + 1)
    ax.tick_params(labelleft=False)
    plt.bar(x, pmf.iloc[i, :])
    plt.ylabel("p(x, y={})".format(y), rotation=0, labelpad=30)
    plt.ylim(0, 0.15)
    plt.xticks(range(6), ['A', 'B', 'C', 'D', 'E', 'F'])

plt.suptitle("y가 주어진 경우의 결합확률질량함수의 단면", y=1.05)
plt.tight_layout()
plt.show()

연습 문제 7.4.3¶

위에서 구한 데이터를 기준으로 다음 질문에 답하라.

만약 확률변수 \(Y\)의 값이 A가 나왔다면 확률변수 \(X\)의 값은 어떤 값이 나올 가능성이 가장 높은가.
만약 확률변수 \(Y\)의 값이 C가 나왔다면 확률변수 \(X\)의 값은 어떤 값이 나올 가능성이 가장 높은가.

**조건부확률질량함수(conditional probability mass function)**는 다변수 확률변수 중 하나의 값이 특정 값으로 고정되어 상수가 되어 버린 경우, 나머지 변수에 대한 확률질량함수를 말한다. 조건부확률질량함수는 다음과 같이 정의된다.

\[ \begin{align} p_{X \mid Y}(x \mid y) = \dfrac{p_{XY}(x, y)}{p_{Y}(y)} \tag{7.4.8} \end{align} \]

\[ \begin{align} p_{Y \mid X}(y \mid x) = \dfrac{p_{XY}(x, y)}{p_{X}(x)} \tag{7.4.9} \end{align} \]

조건부확률질량함수의 모양은 결합질량함수 \(p_{XY}(x, y)\)에서 \(y\)값이 고정된 함수, 즉, 결합질량함수의 단면과 같아진다. 다만 조건부확률질량함수의 합은 1이 된다.

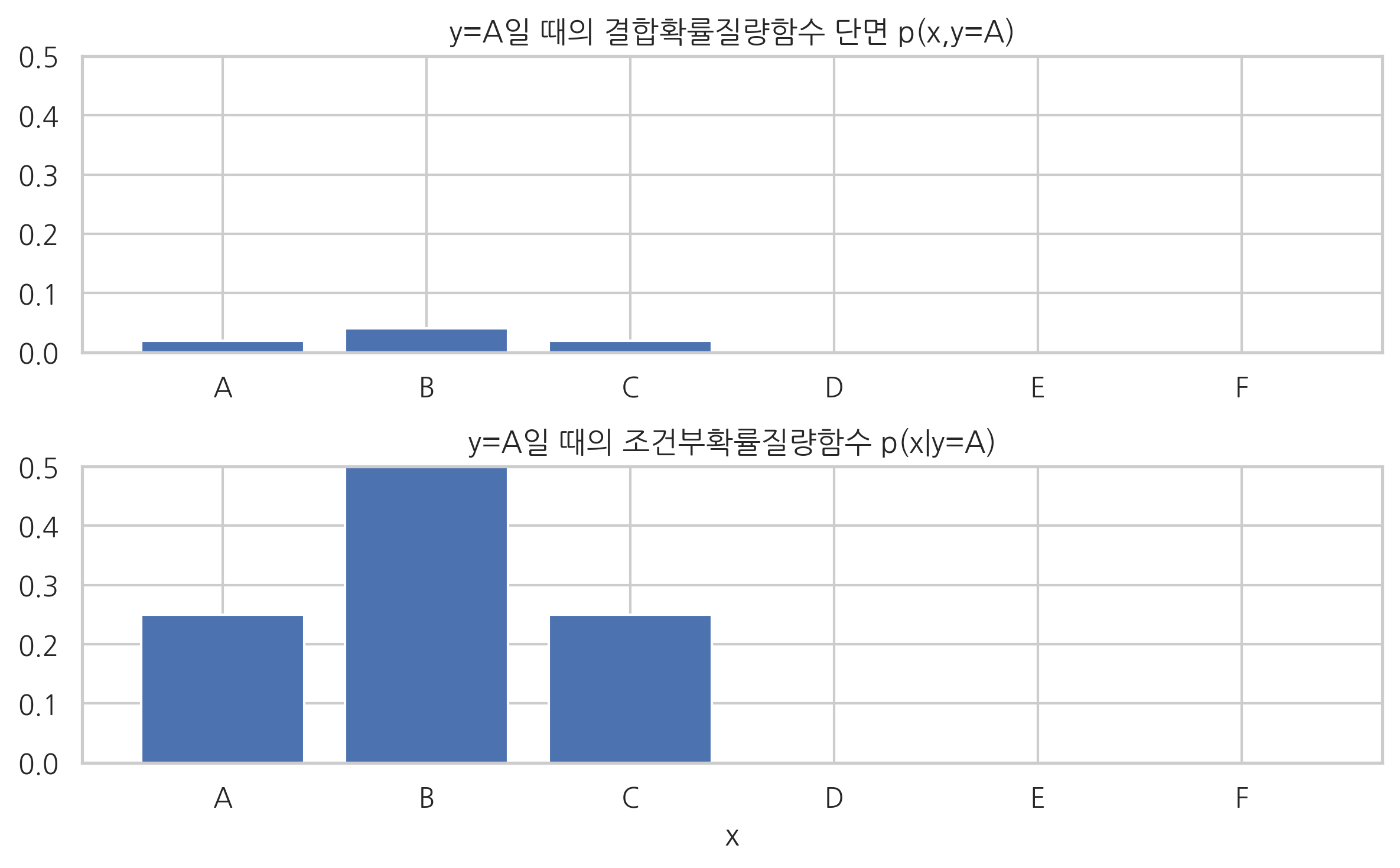
\(y=A\)일 때의 결합확률질량함수의 단면과 확률의 합은 다음과 같다.

pmf.iloc[0, :]

X
A    0.02
B    0.04
C    0.02
D    0.00
E    0.00
F    0.00
Name: A, dtype: float64

np.sum(pmf.iloc[0, :])

0.08

\(y=A\)일 때의 조건부확률질량함수와 확률의 합은 다음과 같다.

cond_y0 = pmf.iloc[0, :]/pmf_marginal_y[0]
cond_y0

X
A    0.25
B    0.50
C    0.25
D    0.00
E    0.00
F    0.00
Name: A, dtype: float64

np.sum(cond_y0)

1.0

plt.subplot(211)
plt.bar(x, pmf.iloc[0, :])
plt.ylim(0, 0.5)
plt.xticks(range(6), ['A', 'B', 'C', 'D', 'E', 'F'])
plt.title("y=A일 때의 결합확률질량함수 단면 p(x,y=A)")
plt.subplot(212)
plt.bar(x, cond_y0)
plt.ylim(0, 0.5)
plt.xticks(range(6), ['A', 'B', 'C', 'D', 'E', 'F'])
plt.title("y=A일 때의 조건부확률질량함수 p(x|y=A)")
plt.xlabel("x")
plt.tight_layout()
plt.show()

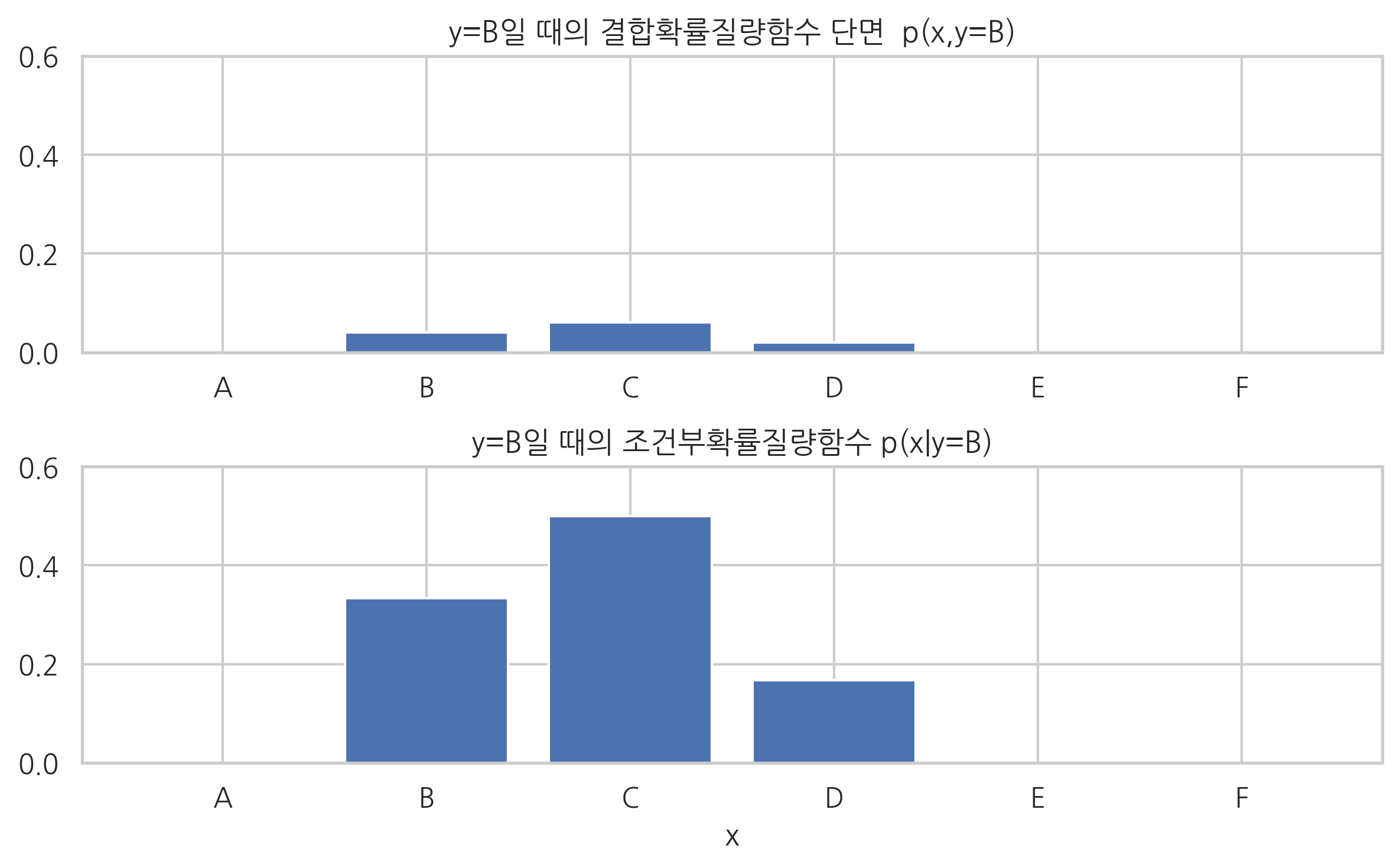
\(y=B\)일 때의 결합확률질량함수의 단면과 확률의 합은 다음과 같다.

pmf.iloc[1, :]

X
A    0.00
B    0.04
C    0.06
D    0.02
E    0.00
F    0.00
Name: B, dtype: float64

np.sum(pmf.iloc[1, :])

0.12000000000000001

\(y=B\)일 때의 조건부확률질량함수와 확률의 합은 다음과 같다.

cond_y1 = pmf.iloc[1, :]/pmf_marginal_y[1]
cond_y1

X
A    0.000000
B    0.333333
C    0.500000
D    0.166667
E    0.000000
F    0.000000
Name: B, dtype: float64

np.sum(cond_y1)

0.9999999999999999

y = np.arange(6)
plt.subplot(211)
plt.bar(y, pmf.iloc[1, :])
plt.ylim(0, 0.6)
plt.xticks(range(6), ['A', 'B', 'C', 'D', 'E', 'F'])
plt.title("y=B일 때의 결합확률질량함수 단면  p(x,y=B)")
plt.subplot(212)
plt.bar(y, cond_y1)
plt.ylim(0, 0.6)
plt.xticks(range(6), ['A', 'B', 'C', 'D', 'E', 'F'])
plt.title("y=B일 때의 조건부확률질량함수 p(x|y=B)")
plt.xlabel("x")
plt.tight_layout()
plt.show()

다변수 연속확률변수¶

연속확률분포에서는 이산확률분포와 같이 단순사건을 이용하여 확률을 정의할 수 없으므로 단변수 연속확률변수처럼 누적확률분포함수를 먼저 정의한 후 이를 미분하여 확률밀도함수를 정의하는 방법을 사용한다.

결합누적확률분포함수¶

두 연속 확률변수 \(X\), \(Y\)에 대한 결합누적확률분포함수 \(p_{XY}(x, y) \)는 다음과 같이 정의한다.

\[ \begin{align} F_{XY}(x, y) = P(\{ X < x \} \cap \{ Y < y \}) = P(\{X < x, Y < y\}) \tag{7.4.10} \end{align} \]

결합누적확률분포함수 \(p_{XY}(x, y) \)는 다음과 같은 특성을 가진다.

\[ \begin{align} F_{XY}(\infty, \infty)=1 \tag{7.4.11} \end{align} \]

\[ \begin{align} F_{XY}(-\infty, y)=F_{XY}(x,-\infty)=0 \tag{7.4.12} \end{align} \]

결합확률밀도함수¶

단변수 확률변수의 경우처럼 결합누적확률분포함수를 미분하여 **결합확률밀도함수(joint probability density function)**를 정의할 수 있다. 독립 변수가 2개이므로 각각에 대해 모두 편미분(partial differentication)해야 한다.

\[ \begin{align} p_{XY} = \dfrac{\partial^2 F_{XY}(x, y)}{\partial x \partial y} \tag{7.4.13} \end{align} \]

결합확률밀도함수를 특정 구간에 대해 적분하면 해당 구간에 대한 확률이 된다.

\[ \begin{align} \int_{x_1}^{x_2} \int_{y_1}^{y_2} p_{XY}(x,y)dxdy = P\big(\{ x_1 \leq X \leq x_2, \; y_1 \leq Y \leq y_2 \}\big) \tag{7.4.14} \end{align} \]

따라서 결합확률밀도함수를 모든 변수에 대해 \(-\infty\)에서 \(\infty\) 까지 적분하면 값이 1이 된다.

\[ \begin{align} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p_{XY}(x,y)dxdy=1 \tag{7.4.15} \end{align} \]

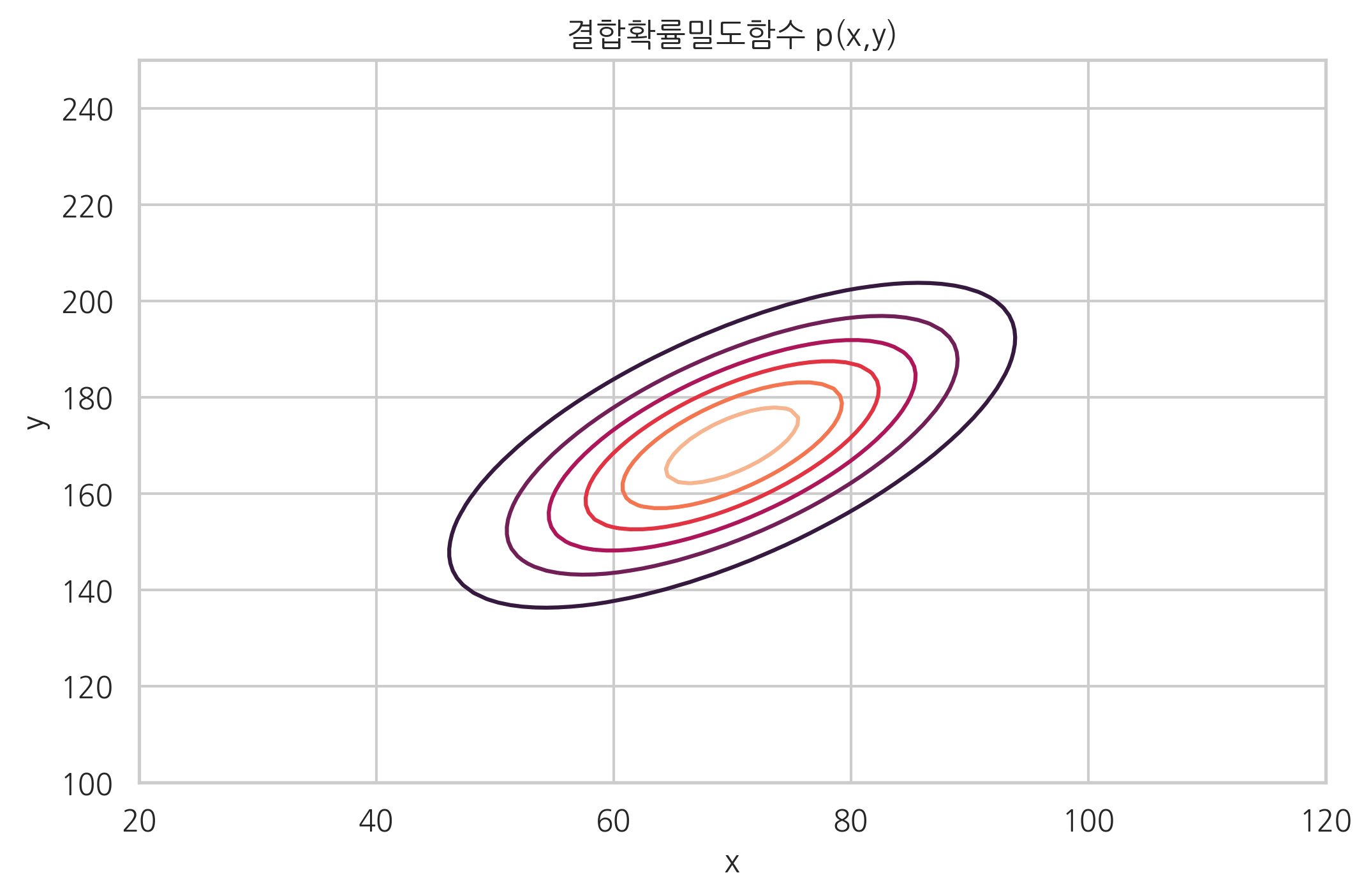
연속 확률변수의 결합확률밀도함수는 2차원 함수가 된다. 아래는 다변수정규분포의 결합확률밀도의 예를 그린 것이다. 어떤 집단에 대해 X는 몸무게, Y는 키를 나타내는 확률변수라고 하자.

mu = [70, 170]
cov = [[150, 140], [140, 300]]
rv = sp.stats.multivariate_normal(mu, cov)

xx = np.linspace(20, 120, 100)
yy = np.linspace(100, 250, 100)
XX, YY = np.meshgrid(xx, yy)
ZZ = rv.pdf(np.dstack([XX, YY]))
plt.contour(XX, YY, ZZ)
plt.xlabel("x")
plt.ylabel("y")
plt.title("결합확률밀도함수 p(x,y)")
plt.show()

주변확률밀도함수¶

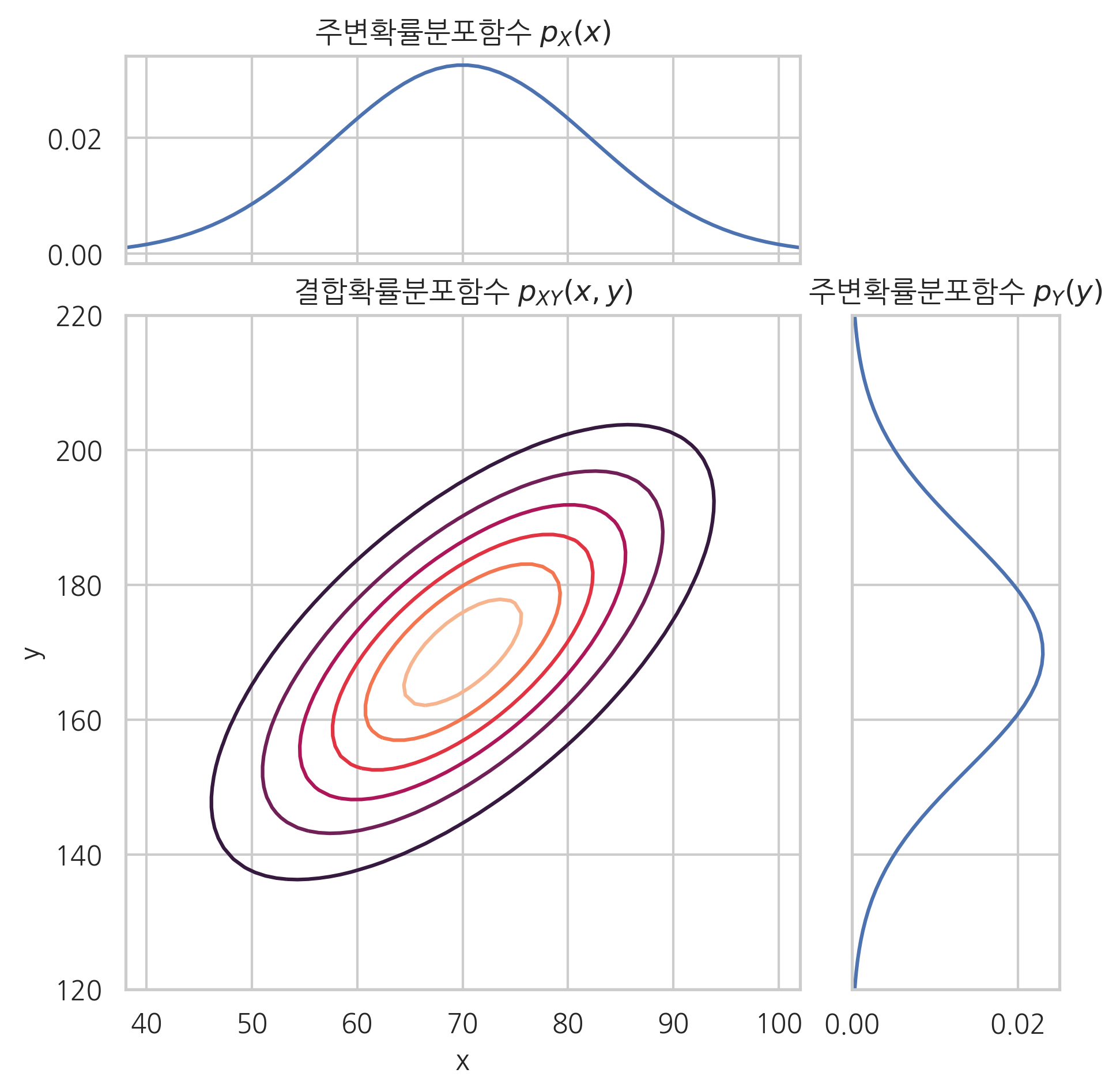
**주변확률밀도함수(marginal probability density function)**는 결합확률밀도함수를 특정한 하나의 변수에 대해 가중평균한 값을 말한다. 따라서 결합확률밀도함수를 하나의 확률변수에 대해서만 적분하여 구한다.

가중평균(적분)으로 인해 차원이 한 개 줄어들기 때문에 2차원 확률변수의 주변 확률 밀도 함수는 1차원 함수가 된다.

\[ \begin{align} p_X(x) = \int_{-\infty}^{\infty} p_{XY}(x,y)dy \tag{7.4.16} \end{align} \]

\[ \begin{align} p_Y(y) = \int_{-\infty}^{\infty} p_{XY}(x,y)dx \tag{7.4.17} \end{align} \]

from matplotlib.ticker import NullFormatter
from matplotlib import transforms
from scipy.integrate import simps  # 심슨법칙(Simpson's rule)을 사용한 적분 계산

xx = np.linspace(20, 120, 100)
yy = np.linspace(100, 250, 100)
XX, YY = np.meshgrid(xx, yy)
ZZ = rv.pdf(np.dstack([XX, YY]))
fx = [simps(Z, yy) for Z in ZZ.T]
fy = [simps(Z, xx) for Z in ZZ]

plt.figure(figsize=(6, 6))

left, width = 0.1, 0.65
bottom, height = 0.1, 0.65
bottom_h = left_h = left + width + 0.05

rect1 = [left, bottom, width, height]
rect2 = [left, bottom_h, width, 0.2]
rect3 = [left_h, bottom, 0.2, height]

ax1 = plt.axes(rect1)
ax2 = plt.axes(rect2)
ax3 = plt.axes(rect3)

ax2.xaxis.set_major_formatter(NullFormatter())
ax3.yaxis.set_major_formatter(NullFormatter())

ax1.contour(XX, YY, ZZ)
ax1.set_title("결합확률분포함수 $p_{XY}(x, y)$")
ax1.set_xlabel("x")
ax1.set_ylabel("y")

ax2.plot(xx, fx)
ax2.set_title("주변확률분포함수 $p_X(x)$")

base = ax3.transData
rot = transforms.Affine2D().rotate_deg(-90)
plt.plot(-yy, fy, transform=rot + base)
plt.title("주변확률분포함수 $p_Y(y)$")

ax1.set_xlim(38, 102)
ax1.set_ylim(120, 220)
ax2.set_xlim(38, 102)
ax3.set_xlim(0, 0.025)
ax3.set_ylim(120, 220)

plt.show()

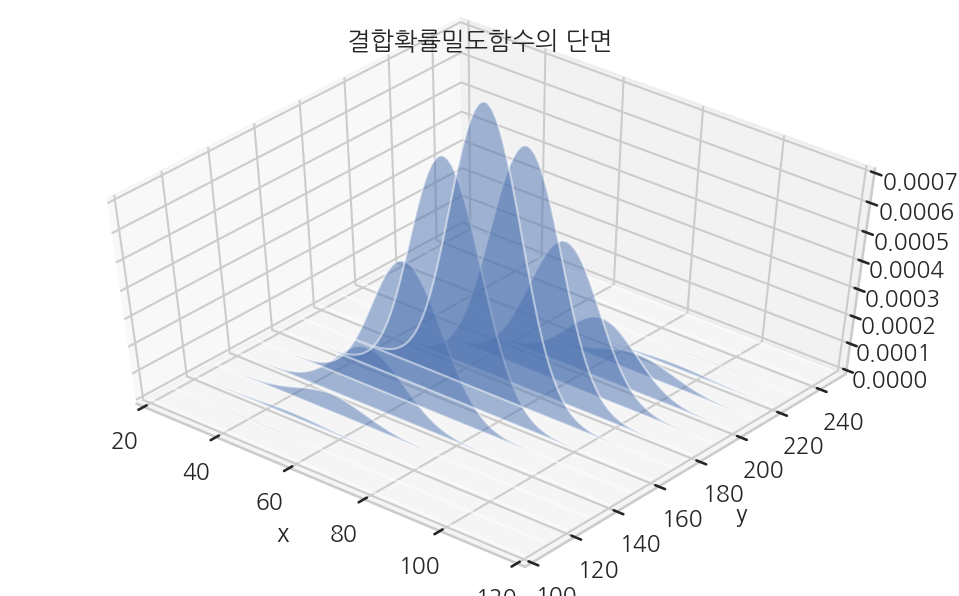
조건부확률밀도함수¶

고정된 y값에 대해 확률 밀도 함수의 단면을 표시하면 다음과 같다.

from matplotlib.collections import PolyCollection
from matplotlib import colors as mcolors

xx = np.linspace(20, 120, 100)
yy = np.linspace(100, 250, 16)
XX, YY = np.meshgrid(xx, yy)
ZZ = rv.pdf(np.dstack([XX, YY]))

fig = plt.figure(dpi=150)
ax = fig.gca(projection='3d')

xs = np.hstack([0, xx, 0])
zs = np.zeros_like(xs)
verts = []
for i, y in enumerate(yy):
    zs[1:-1] = ZZ[i]
    verts.append(list(zip(xx, zs)))

poly = PolyCollection(verts)
poly.set_alpha(0.5)
ax.add_collection3d(poly, zs=yy, zdir='y')

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(20, 120)
ax.set_ylim(100, 250)
ax.set_zlim3d(0, 0.0007)
ax.view_init(50, -50)
plt.title("결합확률밀도함수의 단면")
plt.show()

for i, j in enumerate(range(9, 3, -1)):
    ax = plt.subplot(6, 1, i + 1)
    ax.tick_params(labelleft=False)
    plt.plot(xx, ZZ[j, :])
    plt.ylim(0, 0.0012)
    if i < 5:
        ax.xaxis.set_ticklabels([])
    plt.ylabel("p(x, y={:.0f})".format(yy[j]), rotation=0, labelpad=40)
plt.xlabel("x")
plt.tight_layout()
plt.suptitle("결합확률밀도함수의 단면", y=1.05)
plt.show()

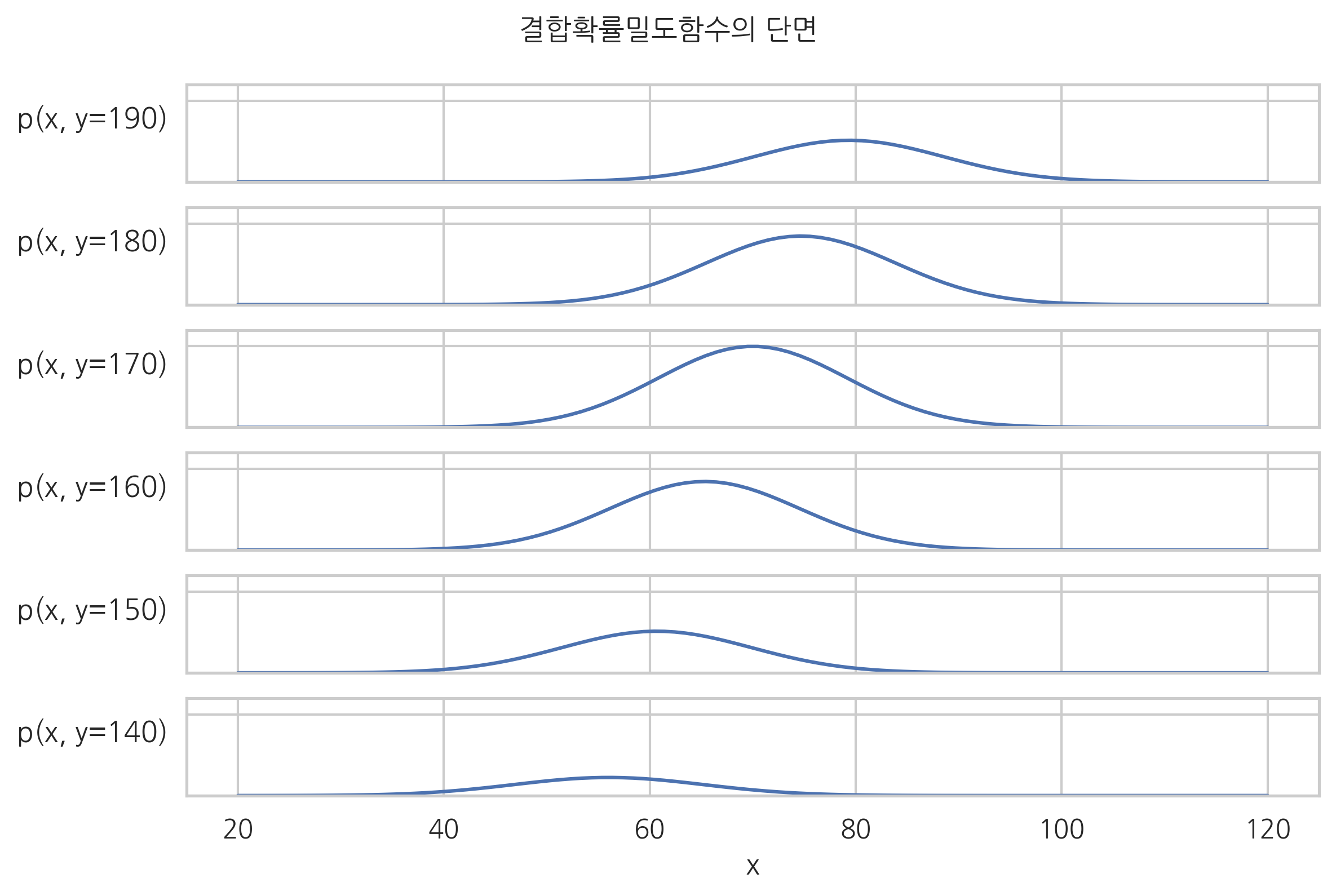
연습 문제 7.4.4¶

확률변수의 값을 모른다고 할 때 어떤 값이 나올 가능성이 가장 높은가.
만약 확률변수 Y 의 값이 170이 나왔다면 확률변수 X 의 값은 어떤 값이 나올 가능성이 가장 높은가.
만약 확률변수 Y 의 값이 150이 나왔다면 확률변수 X 의 값은 어떤 값이 나올 가능성이 가장 높은가.

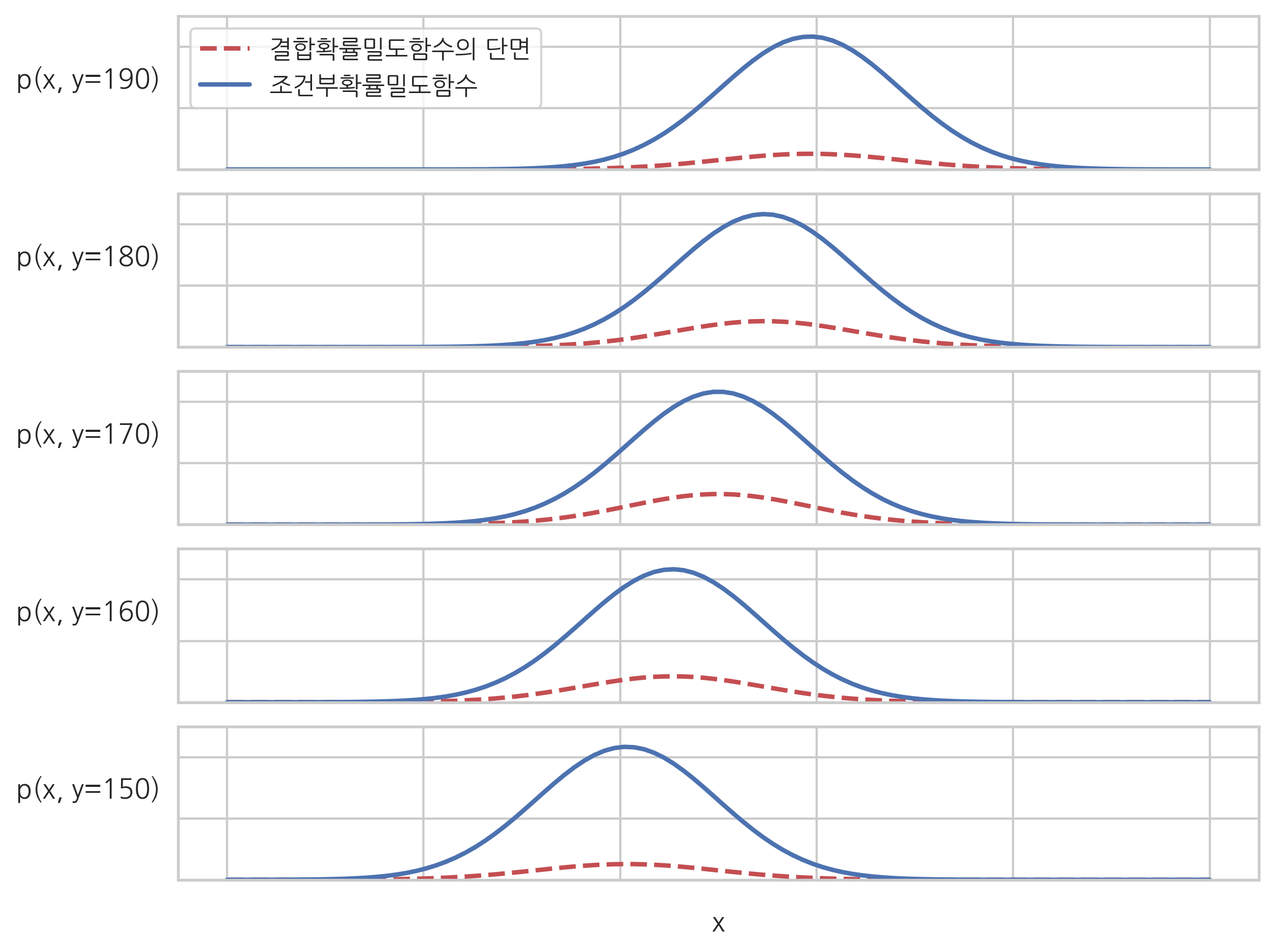
**조건부확률밀도함수(conditional probability density function)**는 다변수 확률변수 중 하나의 값이 특정 값이라는 사실이 알려진 경우, 이러한 조건(가정)에 의해 변화한 나머지 확률변수에 대한 확률밀도함수를 말한다.

\[ \begin{align} p_{X \mid Y}(x \mid y) = \dfrac{p_{XY}(x, y)}{p_{Y}(y)} \tag{7.4.18} \end{align} \]

\[ \begin{align} p_{Y \mid X}(y \mid x) = \dfrac{p_{XY}(x, y)}{p_{X}(x)} \tag{7.4.19} \end{align} \]

조건부확률밀도함수에서 조건이 되는 확률변수의 값은 특정한 값으로 고정되어 있으므로 변수가 아니라 모수로 생각할 수 있다. 예를 들어 \(p_{X \mid Y}(x \mid y)\)에서 \(y\)의 값은 고정되어 있으므로 이 값은 \(x\)의 함수가 된다.

from scipy.integrate import simps  # 심슨법칙(Simpson's rule)을 사용한 적분 계산

mag = 10 # 확대 비율
xx = np.linspace(20, 120, 100)
yy = np.linspace(100, 250, 16)
XX, YY = np.meshgrid(xx, yy)
ZZ = rv.pdf(np.dstack([XX, YY]))
plt.figure(figsize=(8, 6))
for i, j in enumerate(range(9, 4, -1)):
    ax = plt.subplot(5, 1, i + 1)
    ax.tick_params(labelleft=False)
    plt.plot(xx, ZZ[j, :] * mag, 'r--', lw=2, label="결합확률밀도함수의 단면")
    marginal = simps(ZZ[j, :], xx)
    plt.plot(xx, ZZ[j, :] / marginal, 'b-', lw=2, label="조건부확률밀도함수")
    plt.ylim(0, 0.05)
    ax.xaxis.set_ticklabels([])
    plt.ylabel("p(x, y={:.0f})".format(yy[j]), rotation=0, labelpad=40)
    if i == 0: 
        plt.legend(loc=2)
plt.xlabel("x")
plt.tight_layout()
plt.show()

독립과 상관¶

두 확률변수가 있을 때, 한 확률변수의 표본 값이 달라지면 다른 확률변수의 조건부 분포가 달라질 때 서로 상관 관계가 있다고 한다. 반대로 두 확률변수가 상관 관계가 아니면 서로 **독립(independent)**이라고 한다. 확률변수의 독립을 수학적으로 정의하면 다음과 같다.

두 확률변수 \(X\), \(Y\)의 결합확률밀도함수(joint pdf)가 주변확률밀도함수(marginal pdf)의 곱과 같으면 서로 독립(independent)이다.

\[ \begin{align} p_{XY}(x, y) = p_X(x)p_Y(y) \tag{7.4.20} \end{align} \]

이 정의는 확률변수가 두 개 보다 많을 때도 적용된다. 예를 들어 세 개의 확률변수 \(X\), \(Y\), \(Z\)의 결합확률밀도함수가 각각의 주변확률밀도함수(marginal pdf)의 곱과 같으면 세 확률변수는 서로 독립이다.

\[ \begin{align} p_{XYZ}(x, y, z) = p_X(x)p_Y(y)p_Z(z) \tag{7.4.21} \end{align} \]

이 때 \(X\), \(Y\), \(Z\) 중 어느 두 확률변수를 골라도 서로 독립이 된다.

\[\begin{split} \begin{align} \begin{aligned} p_{XY}(x, y) &= \sum_{z\in\Omega_z} p_{XY}(x, y, z) \\ &= \sum_{z\in\Omega_z} p_X(x)p_Y(y)p_Z(z) \\ &= p_X(x)p_Y(y) \sum_{z\in\Omega_z} p_Z(z) \\ &=p_X(x)p_Y(y) \end{aligned} \tag{7.4.22} \end{align} \end{split}\]

반복시행¶

같은 확률변수에서 복수의 표본 데이터를 취하는 경우에는 이 표본들은 서로 독립인 확률변수들에서 나온 표본으로 볼 수 있다. 따라서 확률밀도함수가 \(f(x)\)이고 표본 데이터가 \(\{x_1, x_2, x_3, \cdots, x_N \}\)이면 이 데이터, 즉 벡터 \((x_1, x_2, x_3, \cdots, x_N)\)가 나올 확률은 다음과 같다.

\[ \begin{align} p(x_1, x_2, x_3, \cdots, x_N ) = \prod_{i=1}^N p(x_i) \tag{7.4.23} \end{align} \]

조건부 확률분포¶

독립인 두 확률변수 \(X, Y\)의 조건부확률밀도함수는 주변확률밀도함수와 같다.

\[ \begin{align} p_{X \mid Y} (x | y) = \dfrac{p_{XY}(x, y)}{p_{Y}(y)} = \dfrac{p_{X}(x) p_{Y}(y)}{p_{Y}(y)} = p_{X}(x) \tag{7.4.24} \end{align} \]

\[ \begin{align} p_{Y \mid X} (y | x) = \dfrac{p_{XY}(x, y)}{p_{X}(x)} = \dfrac{p_{X}(x) p_{Y}(y)}{p_{X}(x)} = p_{Y}(y) \tag{7.4.25} \end{align} \]

확률변수 \(X\)가 다른 확률변수 \(Y\)에 독립이면 조건부 확률 분포가 조건이 되는 확률변수의 값에 영향을 받지 않는다. 즉, \(Y\) 값이 \(y_1\)일 때와 \(y_2\)일 때의 조건부 확률 분포 \(f(x \mid y_1)\)과 \(f(x \mid y_2)\)이 \(f(x)\)로 같다는 의미이다.

예를 들어 다음과 같은 두 이산 확률변수의 결합 확률 분포를 보자.

pmf1 = np.array([[1, 2,  4, 2, 1],
                 [2, 4,  8, 4, 2],
                 [4, 8, 16, 8, 4],
                 [2, 4,  8, 4, 2],
                 [1, 2,  4, 2, 1]])
pmf1 = pmf1/pmf1.sum()

pmf1_marginal_x = np.round(pmf1.sum(axis=0), 2)
pmf1_marginal_y = np.round(pmf1.sum(axis=1), 2)
pmf1x = pmf1_marginal_x * pmf1_marginal_y[:, np.newaxis]

plt.subplot(121)
sns.heatmap(pmf1, cmap=mpl.cm.bone_r, annot=True, square=True, linewidth=1, linecolor="k",
            cbar=False, xticklabels=pmf1_marginal_x, yticklabels=pmf1_marginal_y)
plt.title("독립인 두 확률변수의 결합확률질량함수")

plt.subplot(122)
pmf1x = pmf1_marginal_x * pmf1_marginal_y[:, np.newaxis]
sns.heatmap(pmf1x, cmap=mpl.cm.bone_r, annot=True, square=True, linewidth=1, linecolor="k",
            cbar=False, xticklabels=pmf1_marginal_x, yticklabels=pmf1_marginal_y)
plt.title("두 확률변수의 주변확률질량함수의 곱")

plt.show()

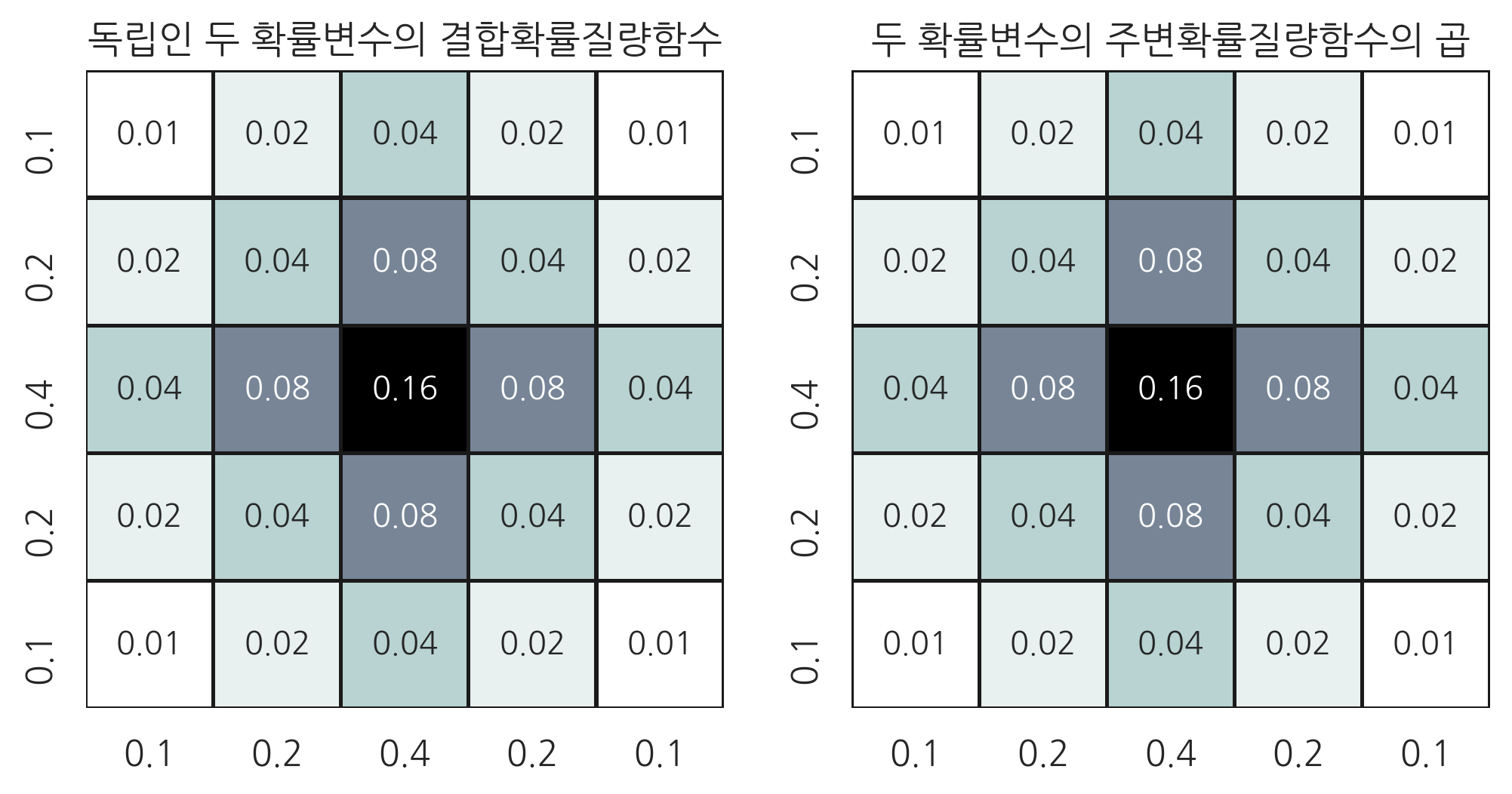
여러 가지 Y값을 바꾸어도 조건부 확률은 변하지 않는 것을 확인할 수 있다.

cond_x_y0 = pmf1[0, :]/pmf1_marginal_y[0]
cond_x_y0

array([0.1, 0.2, 0.4, 0.2, 0.1])

cond_x_y1 = pmf1[1, :]/pmf1_marginal_y[1]
cond_x_y1

array([0.1, 0.2, 0.4, 0.2, 0.1])

이번에는 다음과 같은 상관관계가 있는 두 확률변수를 보자.

pmf2 = np.array([[0, 0,  0, 5, 5],
                 [0, 5,  5, 5, 5],
                 [0, 5, 30, 5, 0],
                 [5, 5,  5, 5, 0],
                 [5, 5,  0, 0, 0]])
pmf2 = pmf2/pmf2.sum()

pmf2_marginal_x = np.round(pmf2.sum(axis=0), 2)
pmf2_marginal_y = np.round(pmf2.sum(axis=1), 2)

plt.subplot(121)
sns.heatmap(pmf2, cmap=mpl.cm.bone_r, annot=True, square=True, linewidth=1, linecolor="k",
            cbar=False, xticklabels=pmf2_marginal_x, yticklabels=pmf2_marginal_y)
plt.title("상관관계인 두 확률변수의 결합확률질량함수")

plt.subplot(122)
pmf2x = pmf2_marginal_x * pmf2_marginal_y[:, np.newaxis]
sns.heatmap(pmf2x, cmap=mpl.cm.bone_r, annot=True, square=True, linewidth=1, linecolor="k",
            cbar=False, xticklabels=pmf2_marginal_x, yticklabels=pmf2_marginal_y)
plt.title("두 확률변수의 주변확률질량함수의 곱")

plt.show()

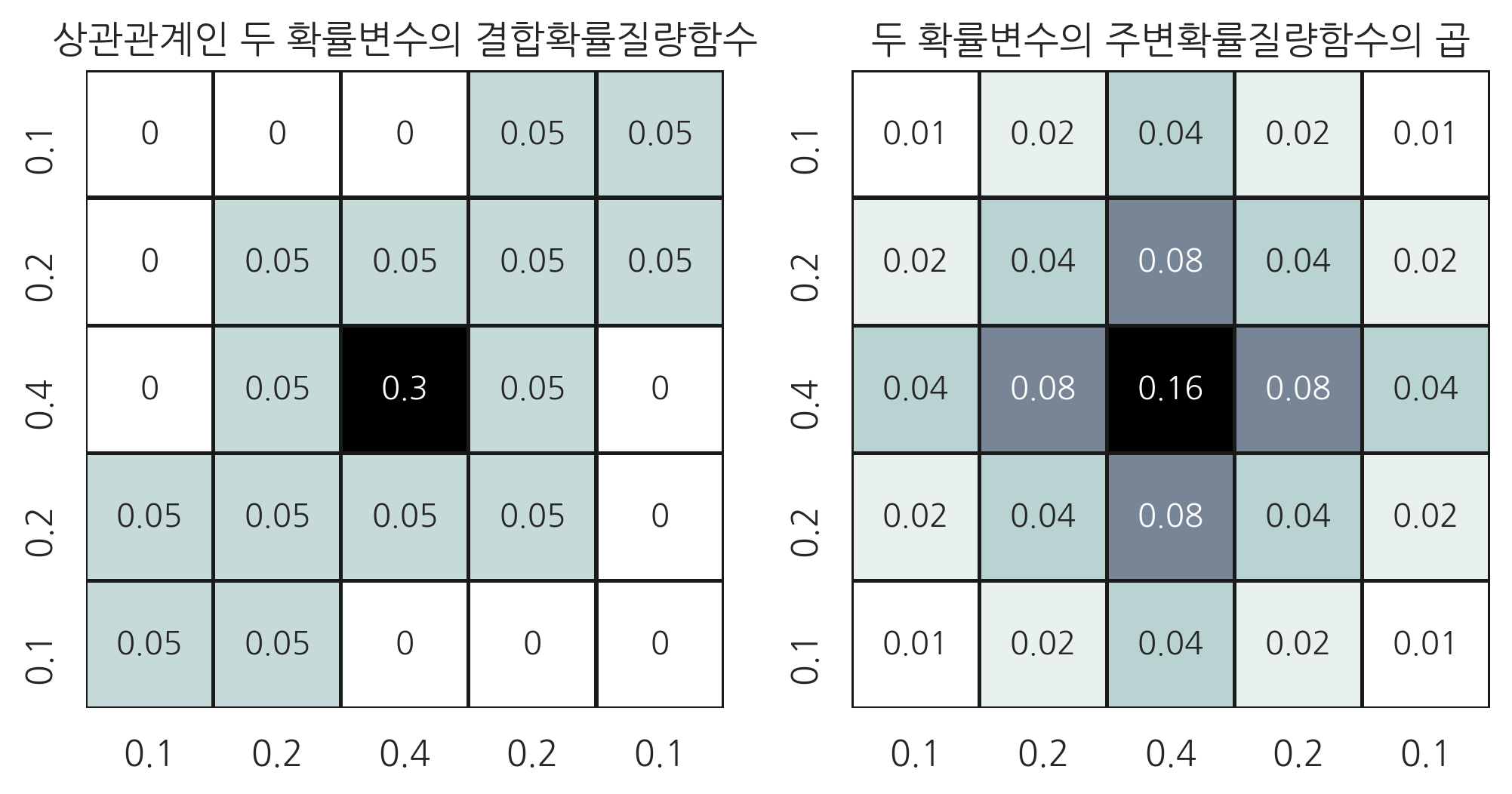
주변 확률분포는 앞의 예와 같지만 \(Y\)의 표본 값에 따라 \(X\)의 조건부 확률분포가 달라지는 것을 확인할 수 있다.

cond_x_y0 = pmf2[0, :]/pmf2_marginal_y[0]
cond_x_y0

array([0. , 0. , 0. , 0.5, 0.5])

cond_x_y1 = pmf2[1, :]/pmf2_marginal_y[1]
cond_x_y1

array([0.  , 0.25, 0.25, 0.25, 0.25])

독립 확률변수의 기댓값¶

독립인 두 확률변수 \(X, Y\)의 기댓값은 다음 성질을 만족한다.

\[ \begin{align} \text{E}[XY] = \text{E}[X]\text{E}[Y] \tag{7.4.26} \end{align} \]

\[ \begin{align} \text{E}[(X - \mu_X)(Y-\mu_Y)] = 0 \tag{7.4.27} \end{align} \]

(증명)

\[\begin{split} \begin{align} \begin{aligned} \text{E}[XY] &= \iint xy \;p_{XY}(x, y) \; dx dy \\ &= \iint xy \;p_{X}(x)p_{Y}(y) \; dx dy \\ \end{aligned} \tag{7.4.28} \end{align} \end{split}\]

다중적분의 값은 적분을 연속하여 한 값과 같다는 푸비니(Fubini)의 정리에 의해 다음처럼 증명할 수 있다.

\[\begin{split} \begin{align} \begin{aligned} \text{E}[XY] &= \int \left( \int xy \;p_{X}(x)p_{Y}(y) dx \right) dy \\ &= \int \left( y\; p_{Y}(y) \left( \int x\; p_{X}(x) \; dx \right) \right) dy \\ &= \left( \int x\;p_{X}(x) \; dx \right) \left( \int y\;p_{Y}(y) \; dy \right) \\ &= \text{E}[X] \text{E}[Y] \\ \end{aligned} \tag{7.4.29} \end{align} \end{split}\]

이 결과를 이용하여 두번째 등식도 다음처럼 증명한다.

\[\begin{split} \begin{align} \begin{aligned} \text{E}[(X - \mu_X)(Y-\mu_Y)] &= \text{E}\left[XY - \mu_XY-\mu_YX + \mu_X\mu_Y\right] \\ &= \text{E}[XY] - \mu_X\text{E}[Y]-\mu_Y\text{E}[X] + \mu_X\mu_Y \\ &= \text{E}[XY] - \mu_X\mu_Y \\ &= \text{E}[XY] - \text{E}[X]\text{E}[Y] = 0 \end{aligned} \tag{7.4.30} \end{align} \end{split}\]

독립 확률변수의 분산¶

독립인 두 확률변수 \(X, Y\)의 분산은 다음 성질을 만족한다. 바로 앞 절에서 설명한 내용이므로 증명은 생략한다.

\[ \begin{align} \text{Var}[X+Y] = \text{Var}[X] + \text{Var}[Y] \tag{7.4.31} \end{align} \]

데이터 사이언스 스쿨

7.4 다변수 확률변수¶

결합확률질량함수¶

예제¶

연습 문제 7.4.1¶

주변확률질량함수¶

연습 문제 7.4.2¶

조건부확률질량함수¶

연습 문제 7.4.3¶

다변수 연속확률변수¶

결합누적확률분포함수¶

결합확률밀도함수¶

주변확률밀도함수¶

조건부확률밀도함수¶

연습 문제 7.4.4¶

독립과 상관¶

반복시행¶

조건부 확률분포¶

독립 확률변수의 기댓값¶

독립 확률변수의 분산¶