5.3 분류모형¶

분류(classification)문제는 독립변수값이 주어졌을 때 그 값과 가장 연관성이 큰 종속변수값(클래스)을 예측하는 문제이다. 현실적인 문제로 바꾸어 말하면 어떤 표본에 대한 데이터가 주어졌을 때 그 표본이 어떤 카테고리 혹은 클래스에 속하는지를 알아내는 문제이기도 하다. 선택해야 할 카테고리 혹은 클래스가 미리 주어졌다는 점에서 보기가 주어진 객관식 시험 문제를 푸는 것과 비슷하다고 말할 수 있다.

분류모형의 종류¶

분류문제를 푸는 방법을 분류모형이라고 한다. 분류모형은 크게 두 가지 종류로 나눌 수 있다.

하나는 주어진 데이터에 대해(conditionally) 각 카테고리 혹은 클래스가 정답일 조건부확률(conditional probability)를 계산하는 확률적 모형이다. 확률적 모형은 조건부확률을 계산하는 방법에 따라 직접 조건부확률 함수의 모양을 추정하는 확률적 판별(discriminative)모형과 베이즈 정리를 사용하여 간접적으로 조건부확률을 구하는 확률적 생성(generative)모형으로 나누어진다.

다른 하나는 주어진 데이터를 카테고리에 따라 서로 다른 영역으로 나누는 경계면(decision boundary)을 찾아낸 다음 이 경계면으로부터 주어진 데이터가 어느 위치에 있는지를 계산하는 판별함수(discriminant function)를 이용하는 판별함수 모형이다.

아래 표에 여러가지 분류모형과 각 분류모형이 어떤 방법론에 속하는지를 나타내었다.

모형	방법론
LDA/QDA	확률적 생성모형
나이브 베이지안	확률적 생성모형
로지스틱 회귀	확률적 판별모형
의사결정나무	확률적 판별모형
퍼셉트론	판별함수 모형
서포트벡터머신	판별함수 모형
인공신경망	판별함수 모형

확률적 모형¶

출력변수 \(y\)가 \(K\)개의 클래스 \(1, \cdots, K\) 중의 하나의 값을 가진다고 가정하자. 확률적 모형은 다음과 같은 순서로 \(x\)에 대한 클래스를 예측한다.

(1) 입력 \(x\)가 주어졌을 때 \(y\)가 클래스 \(k\)가 될 확률 \(P(y=k \mid x )\)을 모두 계산하고,

\[\begin{split} \begin{eqnarray} P_1 &=& P(y=1 \mid x ) \\ \vdots & & \vdots \\ P_K &=& P(y=K \mid x )\\ \end{eqnarray} \end{split}\]

(2) 이 중에서 가장 확률이 큰 클래스를 선택하는 방법이다.

\[ \hat{y} = \arg\max_{k} P(y=k \mid x ) \]

사이킷런 패키지에서 조건부확률 \(P(y=k|x)\)을 사용하는 분류모형들은 모두 predict_proba 메서드와 predict_log_proba 메서드를 지원한다. 이 메서드들은 독립변수 \(x\)가 주어지면 종속변수 \(y\)의 모든 카테고리 값에 대해 조건부확률 또는 조건부확률의 로그값을 계산한다.

조건부확률을 계산하는 방법은 다음 두 가지가 있다.

생성모형(generative model)
판별모형(discriminative model)

확률적 생성모형¶

생성모형은 먼저 각 클래스 별 특징 데이터의 확률분포 \(P(x \mid y=k)\)을 추정한 다음 베이즈 정리를 사용하여 \(P(y=k|x)\)를 계산하는 방법이다.

\[ P(y=k \mid x) = \dfrac{P(x \mid y=k)P(y=k)}{P(x)} \]

생성모형에서는 전체 확률의 법칙을 이용하여 특징 데이터 \(x\)의 무조건부 확률분포 \(P(x)\)를 구할 수 있다.

\[ P(x) = \sum_{k=1}^K P(x \mid y=k)P(y=k) \]

따라서 새로운 가상의 특징 데이터를 생성해내거나 특징 데이터만으로도 아웃라이어를 판단할 수 있다.

하지만 클래스가 많을 경우 모든 클래스에 대해 \(P(x|y=k)\)를 추정하는 것은 많은 데이터를 필요로 할 뿐더러 최종적으로는 사용하지도 않을 확률분포를 계산하는데 계산량을 너무 많이 필요로 한다는 단점이 있다.

QDA¶

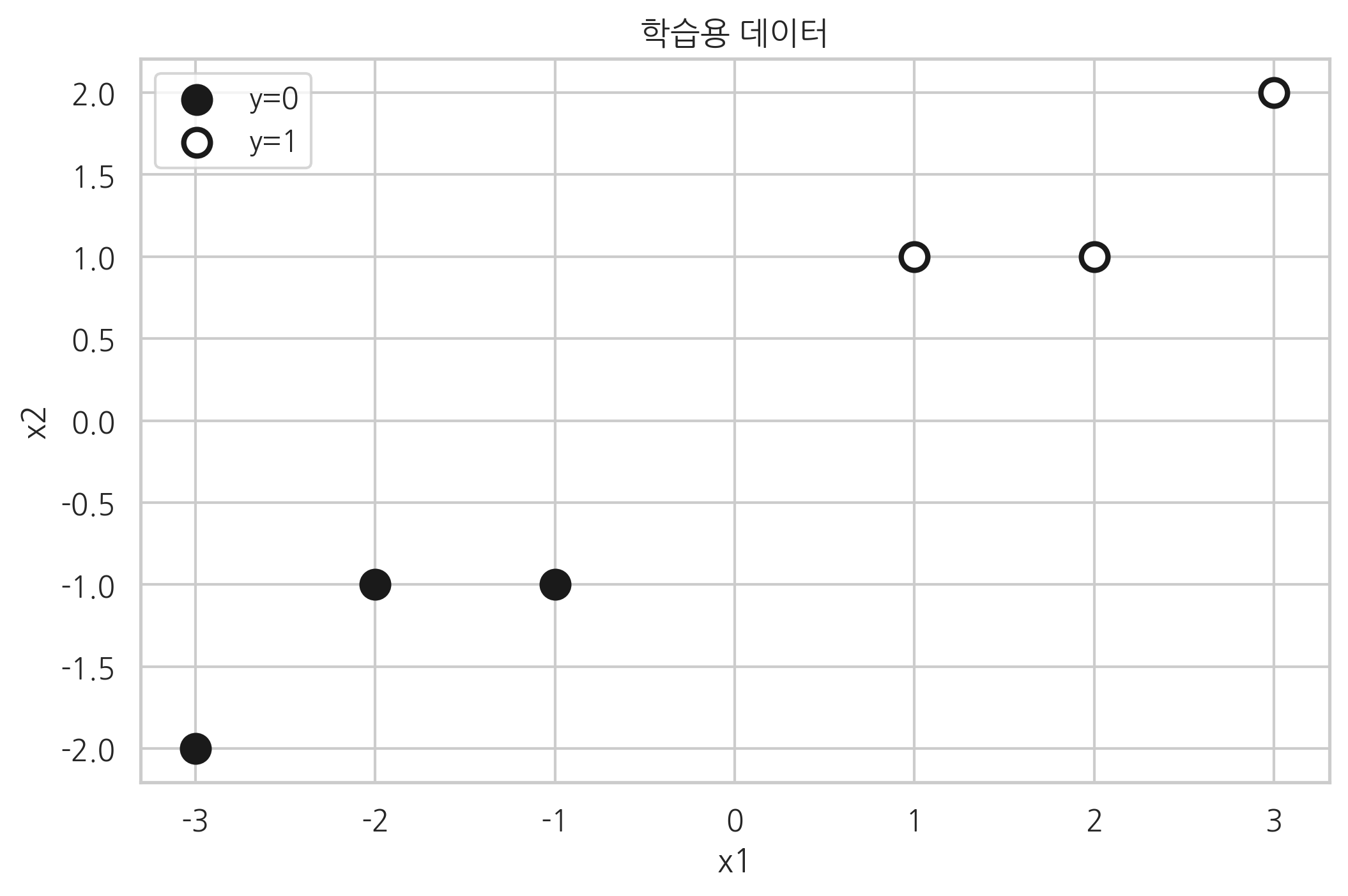
QDA(Quadratic Discriminant Analysis)는 조건부확률 기반 생성(generative) 모형의 하나이다. 예를 들어 다음과 같이 두 가지 클래스의 데이터가 있다고 하자. 스캐터 플롯의 데이터 색은 각 데이터의 클래스를 나타낸다. 검은색은 \(y=0\)인 클래스이고 흰색은 \(y=1\)인 클래스이다. 3개씩으로 이루어진 두 클래스 데이터가 서로 대칭을 이루고 있다는 점에 주의하자.

X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
y = np.array([0, 0, 0, 1, 1, 1])
plt.scatter(X[:3, 0], X[:3, 1], c="k", s=100, edgecolor='k', linewidth=2, label="y=0")
plt.scatter(X[3:, 0], X[3:, 1], c="w", s=100, edgecolor='k', linewidth=2, label="y=1")
plt.title("학습용 데이터")
plt.xlabel("x1")
plt.ylabel("x2")
plt.legend()
plt.show()

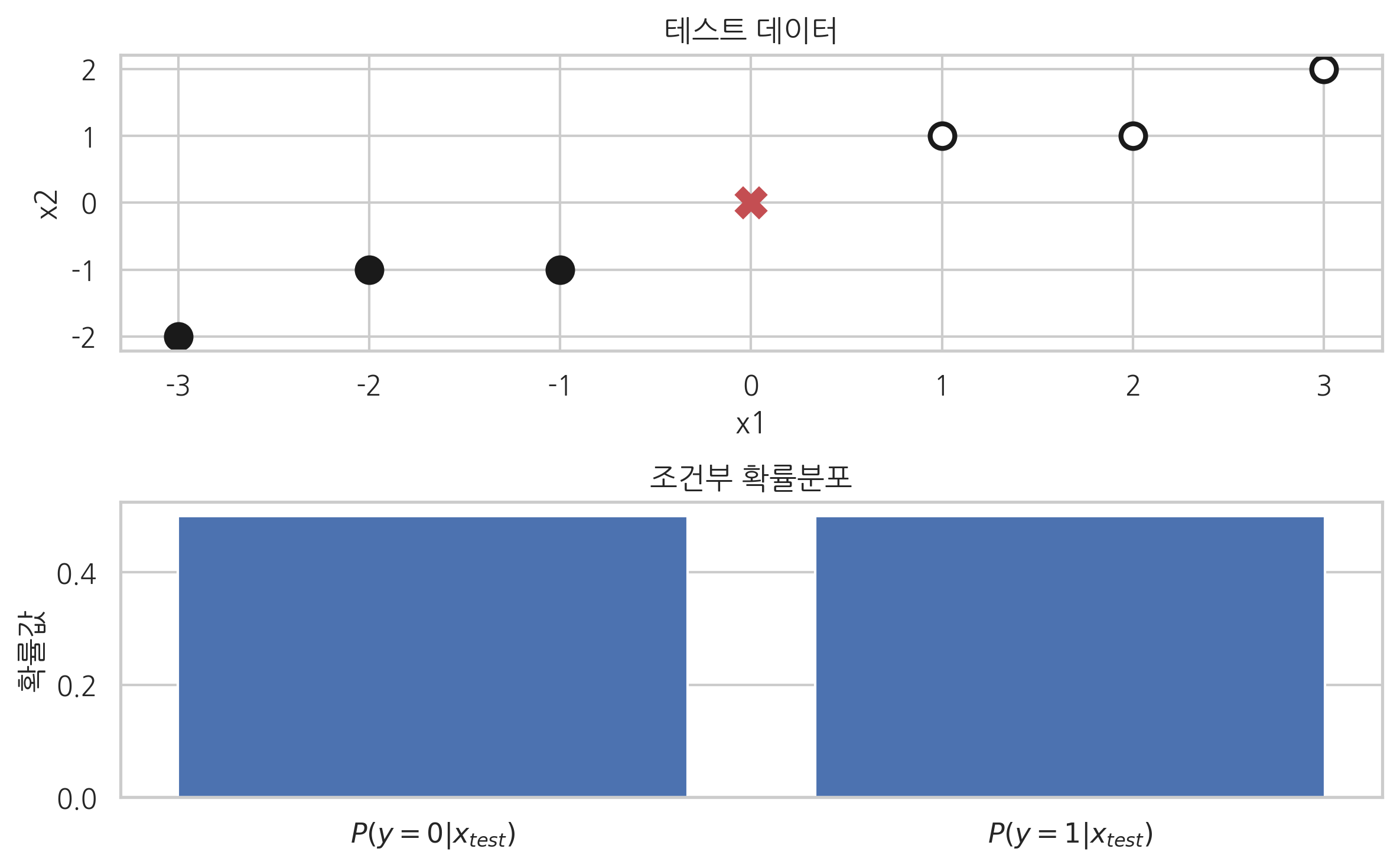
다음 그림들은 이 분류문제를 QDA 방법으로 푼 결과이다. 모형의 자세한 내용과 사이킷런 사용법은 추후 설명하기로 하고 일단 다음과 같은 코드를 사용하면 이 분류문제를 풀 수 있다는 것만 기억하자.

from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis

model = QuadraticDiscriminantAnalysis().fit(X, y)

윗쪽 그림에서 X자로 표시한 것이 테스트 데이터이고, 아래쪽 그램은 이 테스트 데이터가 각 클래스에 속할 조건부확률을 나타낸다. 만약 테스트 데이터가 두 데이터 클래스의 정중앙에 있다면 이 테스트 데이터가 어느 클래스에 속할지 알 수 없으므로 확률이 0.5로 같은 값을 가진다.

x = [[0, 0]]
p = model.predict_proba(x)[0]

plt.subplot(211)
plt.scatter(X[:3, 0], X[:3, 1], c="k", s=100, edgecolor='k', linewidth=2, label="y=0")
plt.scatter(X[3:, 0], X[3:, 1], c="w", s=100, edgecolor='k', linewidth=2, label="y=1")
plt.scatter(x[0][0], x[0][1], c='r', s=100, edgecolor='k', marker='x', linewidth=5)
plt.title("테스트 데이터")
plt.xlabel("x1")
plt.ylabel("x2")
plt.subplot(212)
plt.bar(model.classes_, p)
plt.title("조건부 확률분포")
plt.gca().xaxis.grid(False)
plt.xticks(model.classes_, ["$P(y=0|x_{test})$", "$P(y=1|x_{test})$"])
plt.ylabel("확률값")
plt.tight_layout()
plt.show()

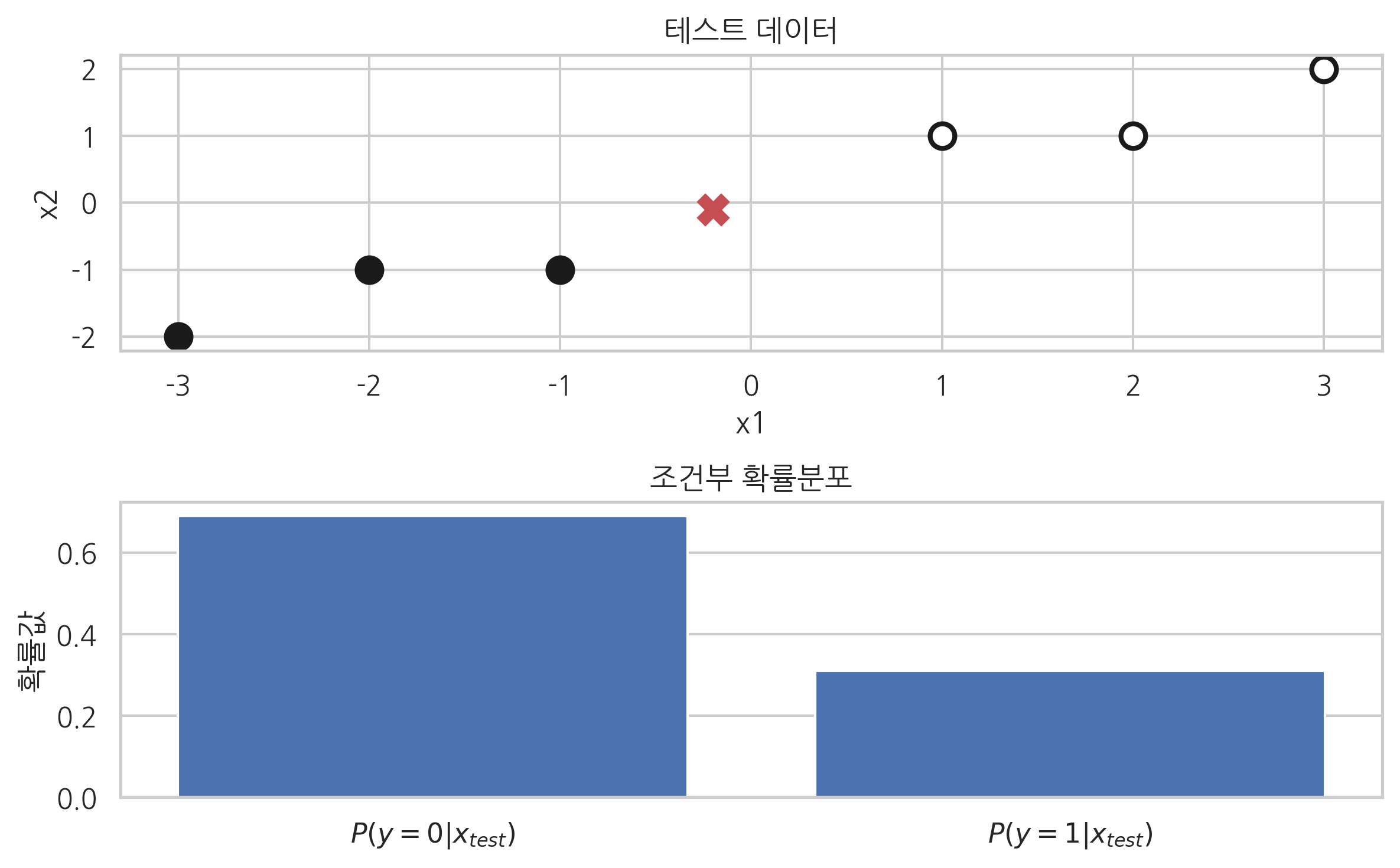
만약 테스트 데이터가 \(y=0\)인 클래스에 더 가깝다면 \(P(y=0|x_{\text{test}})\)가 0.5보다 커지게 된다.

x = [[-0.2, -0.1]]
p = model.predict_proba(x)[0]

plt.subplot(211)
plt.scatter(X[:3, 0], X[:3, 1], c="k", s=100, edgecolor='k', linewidth=2, label="y=0")
plt.scatter(X[3:, 0], X[3:, 1], c="w", s=100, edgecolor='k', linewidth=2, label="y=1")
plt.scatter(x[0][0], x[0][1], c='r', s=100, marker='x', edgecolor='k', linewidth=5)
plt.title("테스트 데이터")
plt.xlabel("x1")
plt.ylabel("x2")
plt.subplot(212)
plt.bar(model.classes_, p)
plt.title("조건부 확률분포")
plt.gca().xaxis.grid(False)
plt.xticks(model.classes_, ["$P(y=0|x_{test})$", "$P(y=1|x_{test})$"])
plt.ylabel("확률값")
plt.tight_layout()
plt.show()

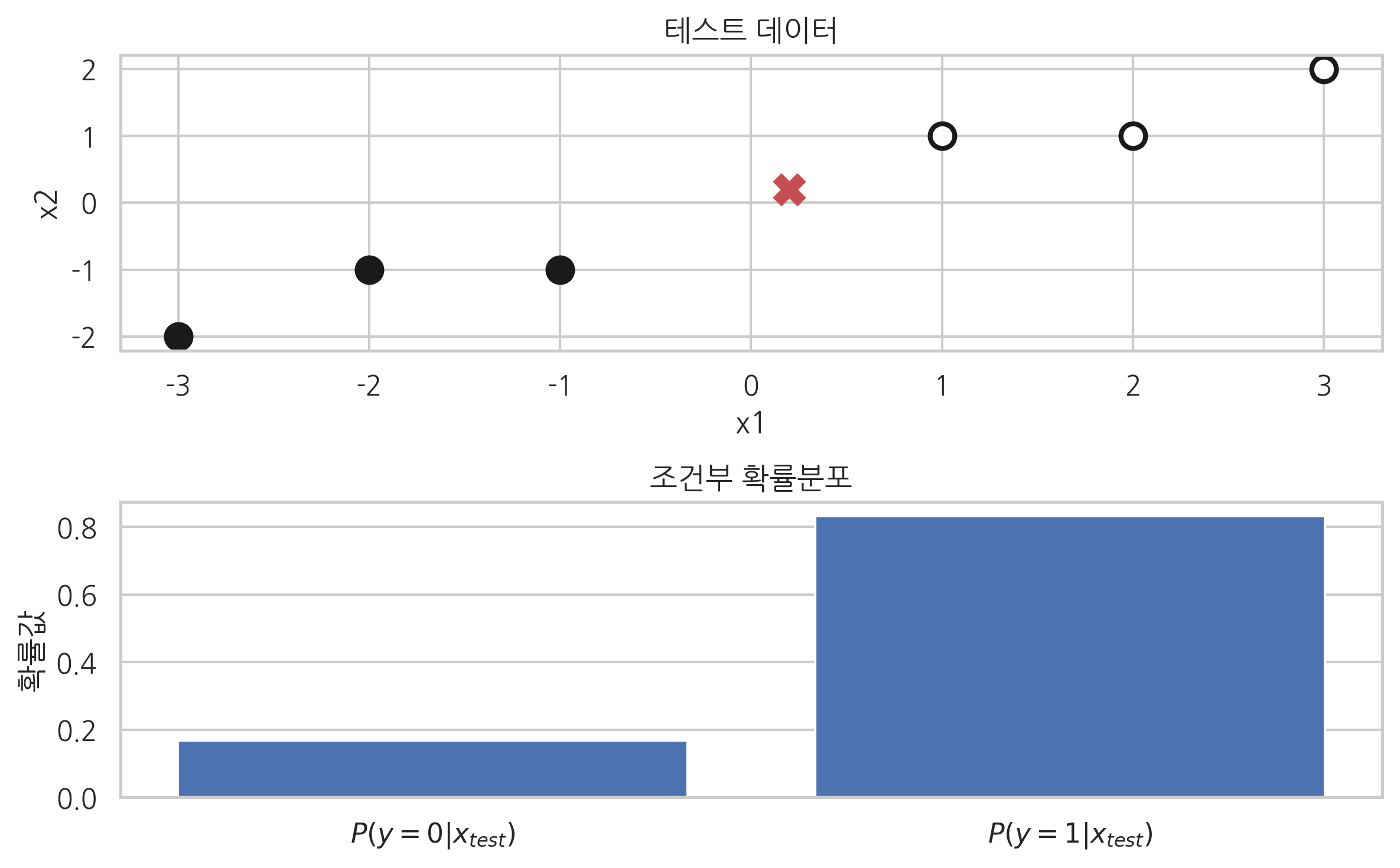
반대로 테스트 데이터가 \(y=1\)인 클래스에 더 가깝다면 \(P(y=1|x_{\text{test}})\)가 0.5보다 커지게 된다.

x = [[0.2, 0.2]]
p = model.predict_proba(x)[0]

plt.subplot(211)
plt.scatter(X[:3, 0], X[:3, 1], c="k", s=100, edgecolor='k', linewidth=2, label="y=0")
plt.scatter(X[3:, 0], X[3:, 1], c="w", s=100, edgecolor='k', linewidth=2, label="y=1")
plt.scatter(x[0][0], x[0][1], c='r', s=100, marker='x', edgecolor='k', linewidth=5)
plt.title("테스트 데이터")
plt.xlabel("x1")
plt.ylabel("x2")
plt.subplot(212)
plt.bar(model.classes_, p)
plt.title("조건부 확률분포")
plt.gca().xaxis.grid(False)
plt.xticks(model.classes_, ["$P(y=0|x_{test})$", "$P(y=1|x_{test})$"])
plt.ylabel("확률값")
plt.tight_layout()
plt.show()

나이브 베이지안 모형¶

조건부확률 기반 생성 모형의 장점 중 하나는 클래스가 3개 이상인 경우에도 바로 적용할 수 있다는 점이다. 나이브 베이지안(Naive Bayesian) 모형도 조건부확률 모형의 일종이다. 아래는 20 뉴스그룹 분류문제를 나이브 베이지안 모형을 사용하여 푼 결과이다.

다음 코드에서는 사이킷런의 TfidfVectorizer 전처리기와 MultinomialNB 모형을 사용하여 20 뉴스그룹 분류문제를 풀었다. TfidfVectorizer 전처리기는 텍스트 데이터를 정해진 크기의 실수 벡터로 변환한다. MultinomialNB 모형은 나이브 베이즈 방법으로 분류문제를 예측한다. 이 두 클래스 객체는 Pipeline을 사용하여 하나의 모형으로 합쳐놓았다. Pipeline으로 합쳐진 모형은 일반적인 모형처럼 fit, predict 등의 메서드를 제공하며 내부의 전처리기의 메소드를 상황에 따라 적절히 호출한다.

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import Pipeline

news = fetch_20newsgroups(subset="all")
model = Pipeline([
    ('vect', TfidfVectorizer(stop_words="english")),
    ('nb', MultinomialNB()),
])
model.fit(news.data, news.target)

n = 1
x = news.data[n:n + 1]
y = model.predict(x)[0]
print(x[0])
print("=" * 80)
print("실제 클래스:", news.target_names[news.target[n]])
print("예측 클래스:", news.target_names[y])

Downloading 20news dataset. This may take a few minutes.
Downloading dataset from https://ndownloader.figshare.com/files/5975967 (14 MB)

From: mblawson@midway.ecn.uoknor.edu (Matthew B Lawson)
Subject: Which high-performance VLB video card?
Summary: Seek recommendations for VLB video card
Nntp-Posting-Host: midway.ecn.uoknor.edu
Organization: Engineering Computer Network, University of Oklahoma, Norman, OK, USA
Keywords: orchid, stealth, vlb
Lines: 21

  My brother is in the market for a high-performance video card that supports
VESA local bus with 1-2MB RAM.  Does anyone have suggestions/ideas on:

  - Diamond Stealth Pro Local Bus

  - Orchid Farenheit 1280

  - ATI Graphics Ultra Pro

  - Any other high-performance VLB card

Please post or email.  Thank you!

  - Matt

-- 
    |  Matthew B. Lawson <------------> (mblawson@essex.ecn.uoknor.edu)  |   
  --+-- "Now I, Nebuchadnezzar, praise and exalt and glorify the King  --+-- 
    |   of heaven, because everything he does is right and all his ways  |   
    |   are just." - Nebuchadnezzar, king of Babylon, 562 B.C.           |   

================================================================================
실제 클래스: comp.sys.ibm.pc.hardware
예측 클래스: comp.sys.ibm.pc.hardware

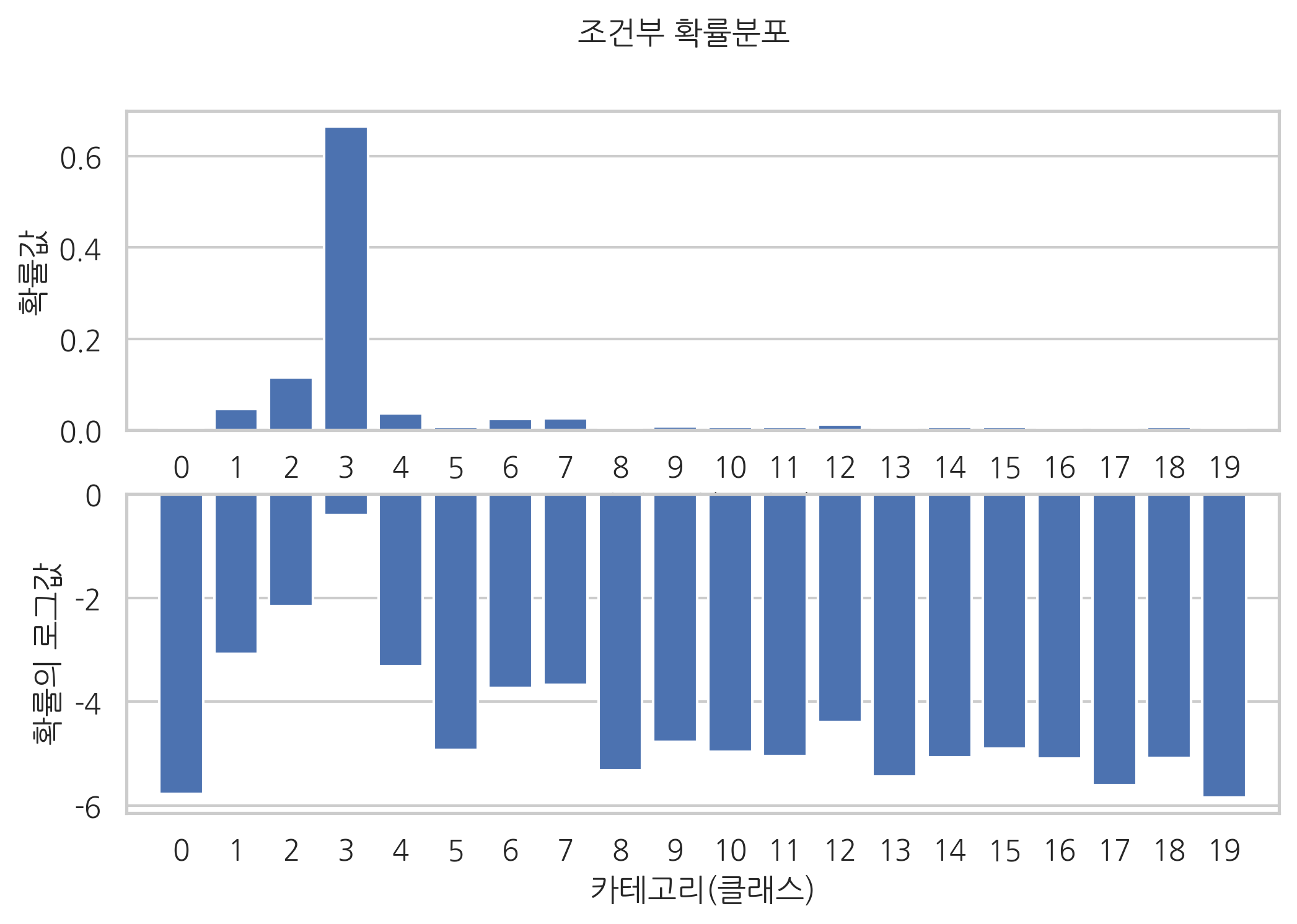
다음 그림은 나이브 베이지안 모형으로 특정한 텍스트 데이터가 20개의 카테고리에 속할 확률을 각각 계산한 것이다. 위쪽 플롯은 확률값이고 아래쪽 플롯은 로그 변환한 값이다.

plt.subplot(211)
plt.bar(model.classes_, model.predict_proba(x)[0])
plt.xlim(-1, 20)
plt.gca().xaxis.grid(False)
plt.xticks(model.classes_)
plt.xlabel("카테고리(클래스)")
plt.ylabel("확률값")
plt.subplot(212)
plt.bar(model.classes_, model.predict_log_proba(x)[0])
plt.xlim(-1, 20)
plt.gca().xaxis.grid(False)
plt.xticks(model.classes_)
plt.xlabel("카테고리(클래스)")
plt.ylabel("확률의 로그값")
plt.suptitle("조건부 확률분포")
plt.show()

확률적 판별 모형¶

위에서 보인 QDA나 나이브 베이지안 방법은 베이즈 정리를 사용하는 조건부확률 기반 생성 모형이었다. 조건부확률 기반 생성 모형은 조건부확률 \(p(y \mid x)\)를 구하기 위해 우선 likelihood \(p(x \mid y)\)를 구하고 베이즈 정리를 사용하여 조건부확률을 계산한다.

하지만 확률론적 판별 모형(probabilistic discriminative model)은 조건부확률 \(p(y=1 \mid x)\)이 \(x\)에 대한 함수 \(f(x)\)로 표시될 수 있다고 가정하고 그 함수를 직접 찾아내는 방법이다.

\[ p(y = k \mid x) = f(x) \]

단, 이 함수 \(f(x)\)는 0보다 같거나 크고 1보다 같거나 작다는 조건을 만족해야 한다.

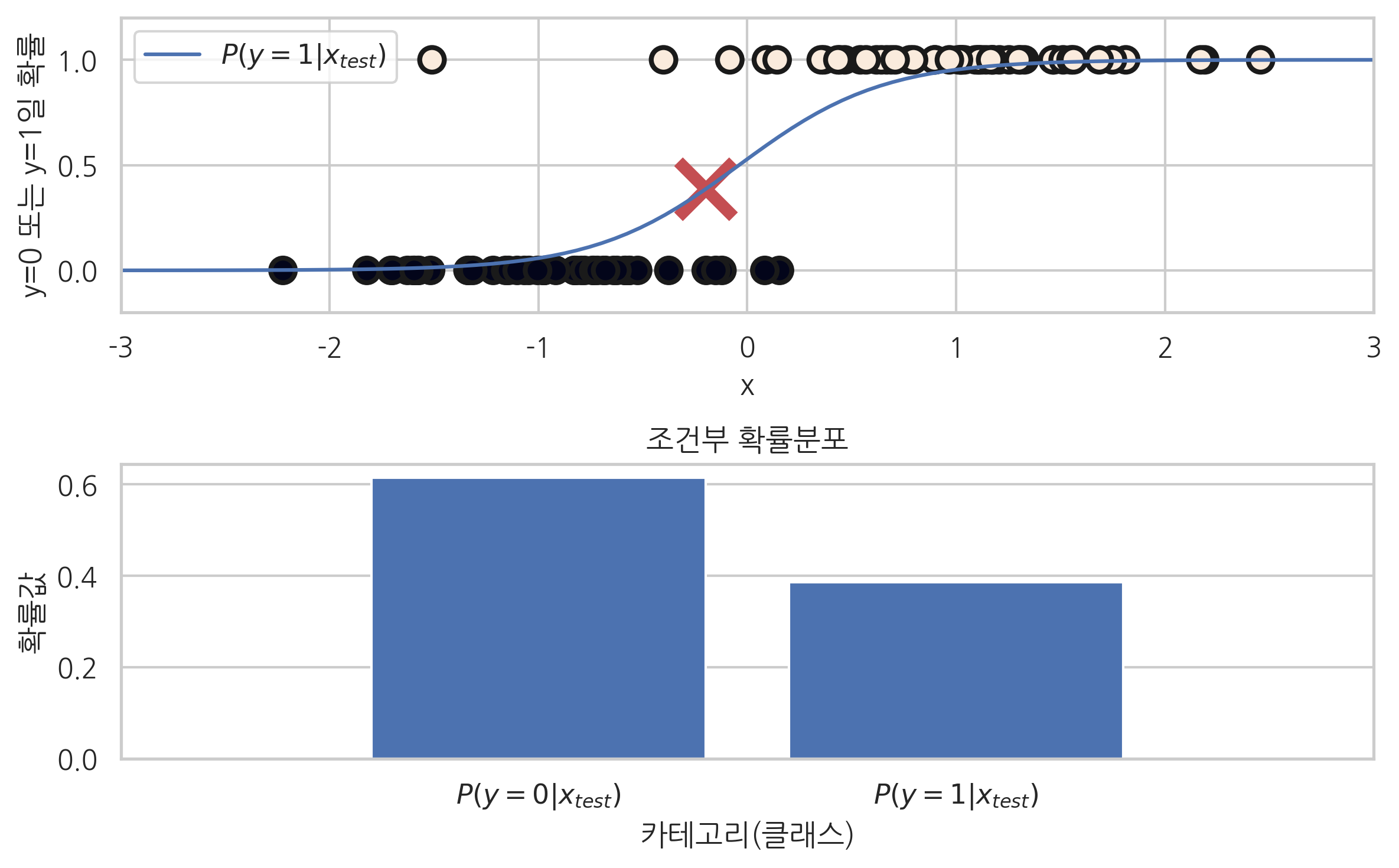
로지스틱 회귀 모형¶

로지스틱 회귀 모형은 확률론적 판별 모형에 속한다.

from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression

X0, y = make_classification(n_features=1, n_redundant=0,
                            n_informative=1, n_clusters_per_class=1, random_state=4)
model = LogisticRegression().fit(X0, y)

xx = np.linspace(-3, 3, 100)
XX = xx[:, np.newaxis]
prob = model.predict_proba(XX)[:, 1]
# prob = 1.0/(1 + np.exp(-model.coef_[0][0]*xx - model.intercept_[0]))

x_test = [[-0.2]]

plt.subplot(211)
plt.plot(xx, prob)
plt.scatter(X0, y, marker='o', c=y, s=100, edgecolor='k', linewidth=2)
plt.scatter(x_test[0], model.predict_proba(x_test)[0][1:], marker='x', s=500, c='r', lw=5)
plt.xlim(-3, 3)
plt.ylim(-.2, 1.2)
plt.xlabel("x")
plt.ylabel("y=0 또는 y=1일 확률")
plt.legend(["$P(y=1|x_{test})$"])
plt.subplot(212)
plt.bar(model.classes_, model.predict_proba(x_test)[0])
plt.xlim(-1, 2)
plt.gca().xaxis.grid(False)
plt.xticks(model.classes_, ["$P(y=0|x_{test})$", "$P(y=1|x_{test})$"])
plt.title("조건부 확률분포")
plt.xlabel("카테고리(클래스)")
plt.ylabel("확률값")
plt.tight_layout()
plt.show()

판별함수 모형¶

또 다른 분류 방법은 동일한 클래스가 모여 있는 영역과 그 영역을 나누는 경계면(boundary plane)을 정의하는 것이다. 이 경계면은 경계면으로부터의 거리를 계산하는 \(f(x)\) 형태의 함수인 **판별함수(discriminant function)**로 정의된다. 판별함수의 값의 부호에 따라 클래스가 나뉘어진다.

\[ \text{판별 경계선}: \;\; f(x) = 0 \]

\[ \text{클래스 1}: \;\; f(x) > 0 \]

\[ \text{클래스 0}: \;\; f(x) < 0 \]

사이킷런에서 판별함수 모형은 판별함수값을 출력하는 decision_function 메서드를 제공한다.

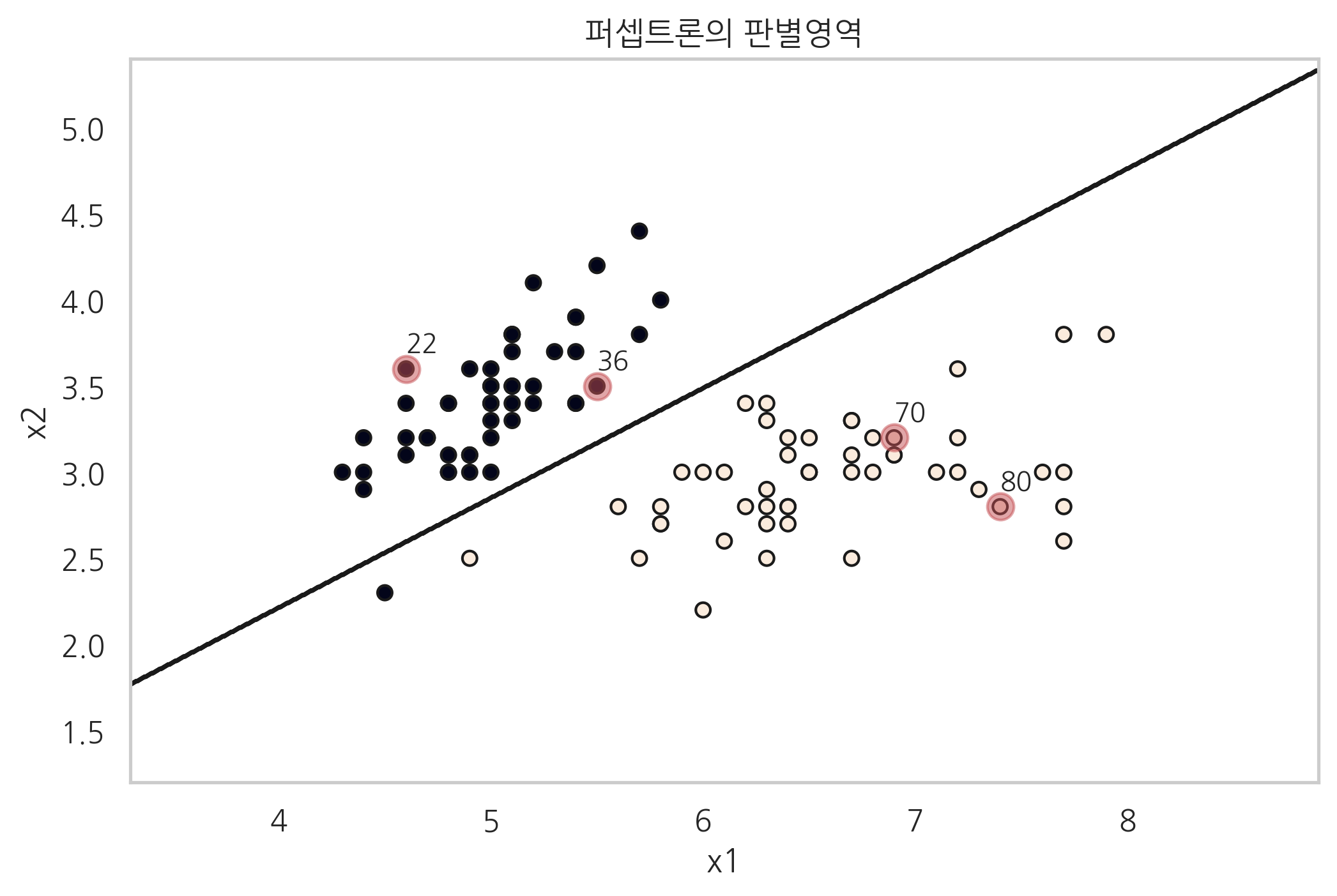
퍼셉트론¶

퍼셉트론(Perceptron)은 가장 단순한 판별함수 모형이다. 다음 그림과 같이 직선이 경계선(boundary line)으로 데이터 영역을 나눈다.

from sklearn.linear_model import Perceptron
from sklearn.datasets import load_iris
iris = load_iris()
idx = np.in1d(iris.target, [0, 2])
X = iris.data[idx, 0:2]
y = iris.target[idx]

model = Perceptron(max_iter=100, eta0=0.1, random_state=1).fit(X, y)
XX_min, XX_max = X[:, 0].min() - 1, X[:, 0].max() + 1
YY_min, YY_max = X[:, 1].min() - 1, X[:, 1].max() + 1
XX, YY = np.meshgrid(np.linspace(XX_min, XX_max, 1000),
                     np.linspace(YY_min, YY_max, 1000))
ZZ = model.predict(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
plt.contour(XX, YY, ZZ, colors='k')
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, edgecolor='k', linewidth=1)

idx = [22, 36, 70, 80]
plt.scatter(X[idx, 0], X[idx, 1], c='r', s=100, alpha=0.5)
for i in idx:
    plt.annotate(i, xy=(X[i, 0], X[i, 1] + 0.1))
plt.grid(False)
plt.title("퍼셉트론의 판별영역")
plt.xlabel("x1")
plt.ylabel("x2")
plt.show()

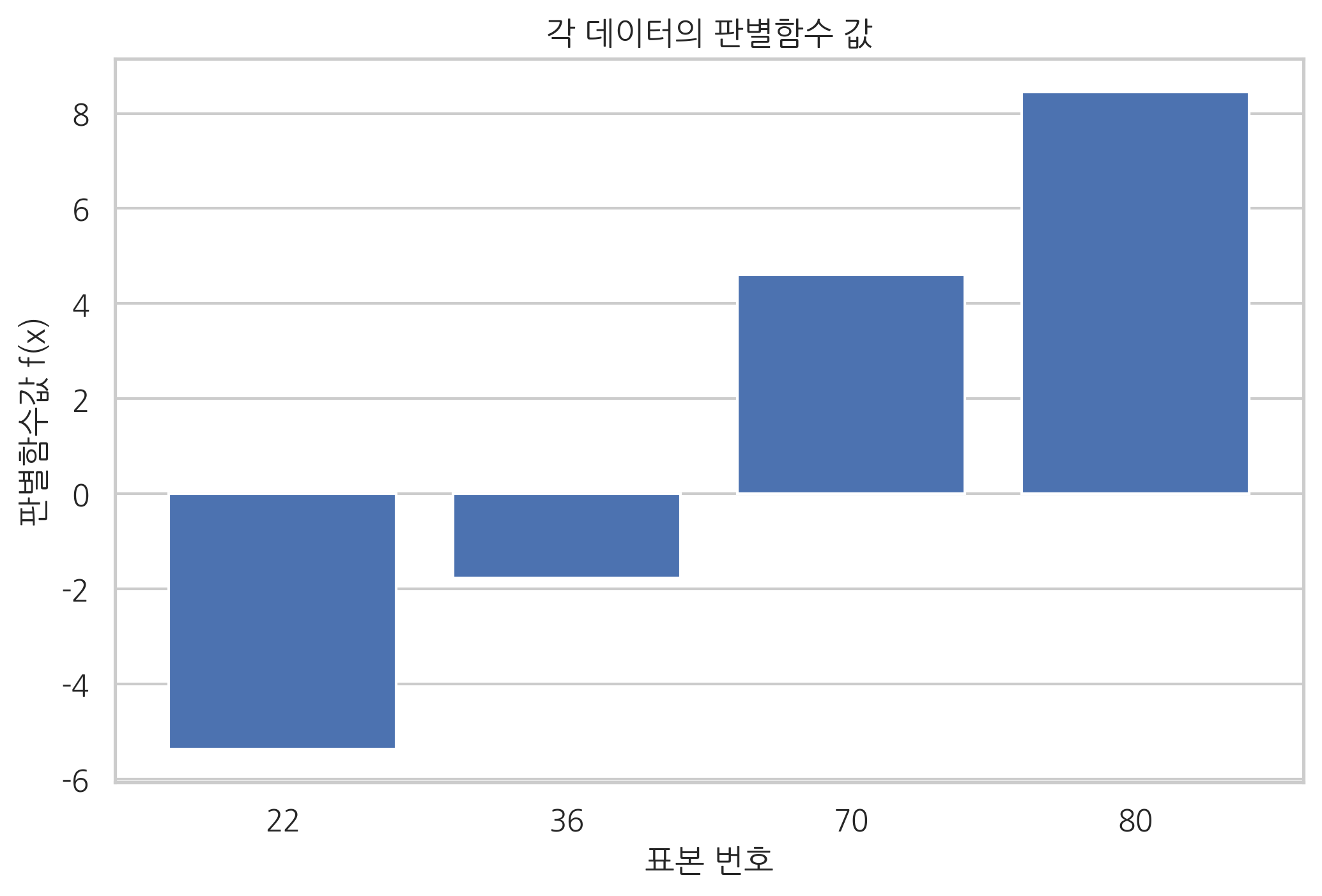
plt.bar(range(len(idx)), model.decision_function(X[idx]))
plt.xticks(range(len(idx)), idx)
plt.gca().xaxis.grid(False)
plt.title("각 데이터의 판별함수 값")
plt.xlabel("표본 번호")
plt.ylabel("판별함수값 f(x)")
plt.show()

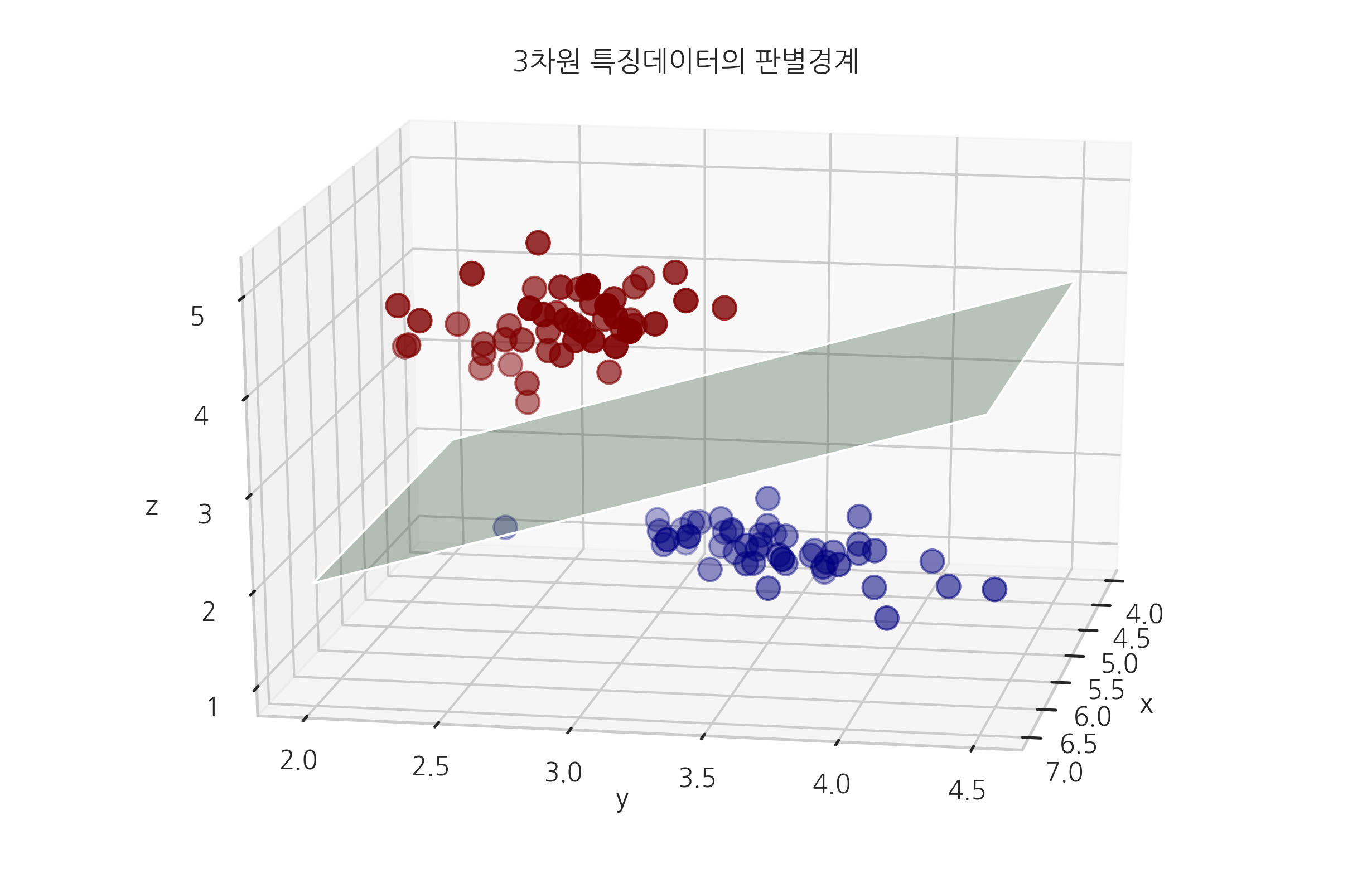
만약 데이터의 차원이 3차원이라면 다음과 같이 경계면(boundary surface)을 가지게 된다. 이러한 경계면이나 경계선을 의사결정 하이퍼 플레인(decision hyperplane)이라고 한다.

from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data[:, :2]
y = iris.target
idx = np.logical_or(iris.target == 0, iris.target == 1)
X = iris.data[idx, :3]
y = iris.target[idx]

fig = plt.figure()
ax = Axes3D(fig, elev=20, azim=10)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, marker='o', s=100, cmap=mpl.cm.jet)
ax.plot_surface(np.array([[4, 4], [7, 7]]), np.array([[2, 4.5], [2, 4.5]]),
                np.array([[2, 4], [2, 4]]), color='g', alpha=.3)
plt.title("3차원 특징데이터의 판별경계")
plt.xlabel("x")
plt.ylabel("y")
ax.set_zlabel("z")
plt.show()

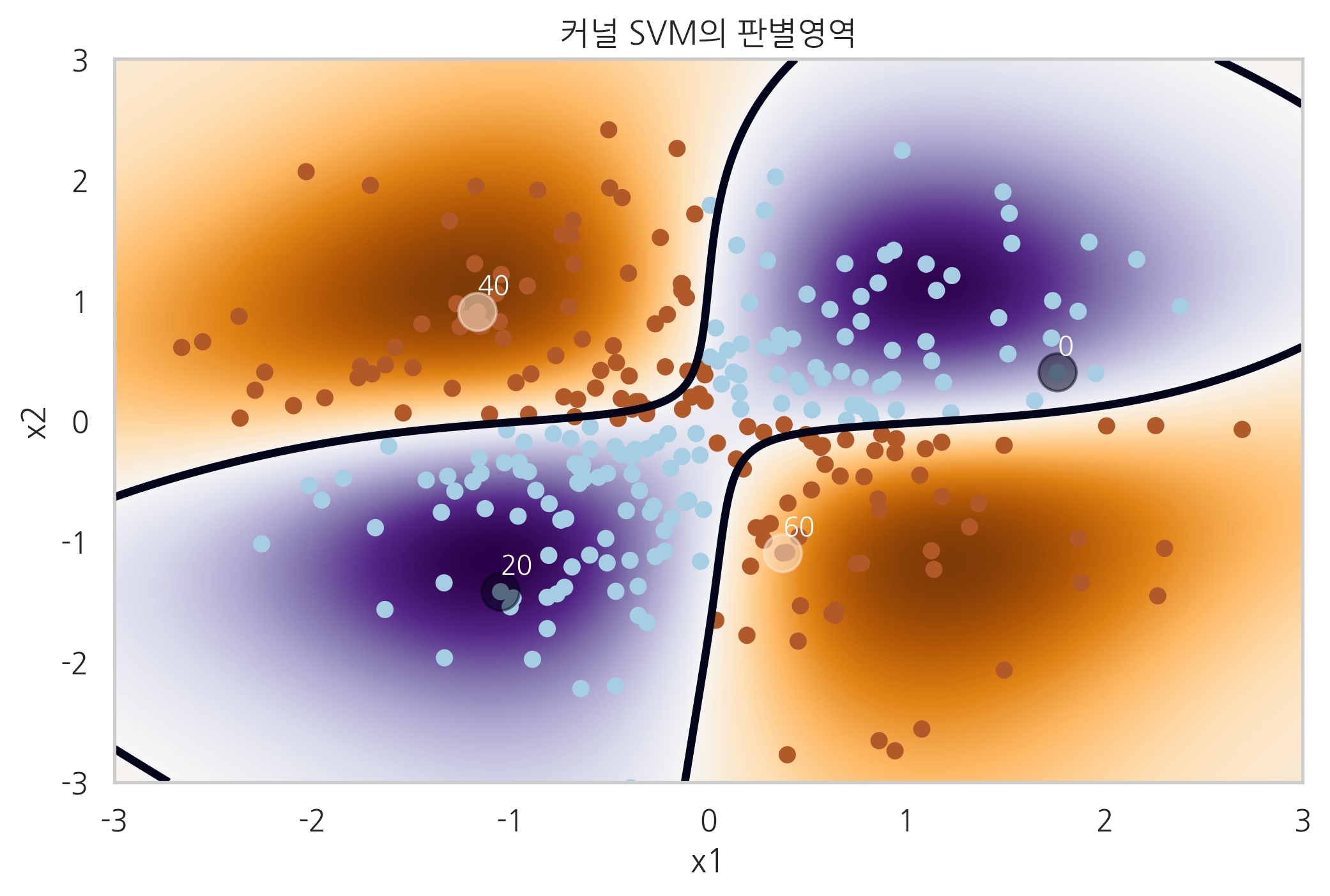
커널 SVM¶

커널 SVM(Kernel Support Vector Machine)을 사용하면 다음과 같이 복잡한 형태의 경계선을 생성할 수도 있다.

from sklearn import svm

xx, yy = np.meshgrid(np.linspace(-3, 3, 500),
                     np.linspace(-3, 3, 500))
np.random.seed(0)
X = np.random.randn(300, 2)
Y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)

model = svm.NuSVC().fit(X, Y)
Z = model.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.imshow(Z, interpolation='nearest',
           extent=(xx.min(), xx.max(), yy.min(), yy.max()), aspect='auto',
           origin='lower', cmap=plt.cm.PuOr_r)
contours = plt.contour(xx, yy, Z, levels=[0], linewidths=3)
plt.scatter(X[:, 0], X[:, 1], s=30, c=Y, cmap=plt.cm.Paired)
idx = [0, 20, 40, 60]
plt.scatter(X[idx, 0], X[idx, 1], c=Y[idx], s=200, alpha=0.5)
for i in idx:
    plt.annotate(i, xy=(X[i, 0], X[i, 1]+0.15), color='white')
plt.grid(False)
plt.axis([-3, 3, -3, 3])
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("커널 SVM의 판별영역")
plt.show()

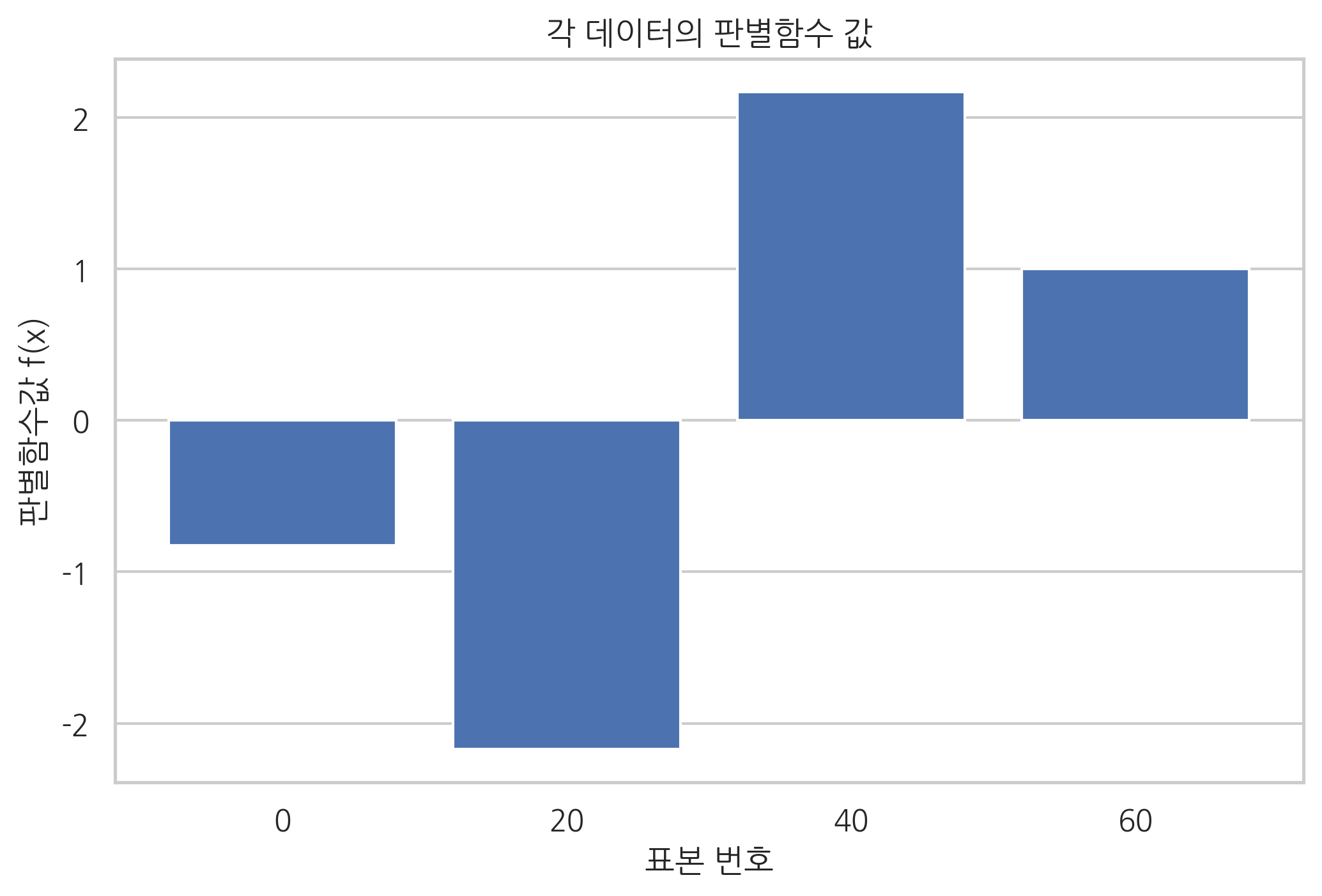
plt.bar(range(len(idx)), model.decision_function(X[idx]))
plt.xticks(range(len(idx)), idx)
plt.gca().xaxis.grid(False)
plt.xlabel("표본 번호")
plt.ylabel("판별함수값 f(x)")
plt.title("각 데이터의 판별함수 값")
plt.show()

다중 클래스 분류¶

확률적 모형은 클래스가 3개 이상인 경우를 다중 클래스(Multi-Class) 분류문제도 풀 수 있지만 판별함수 모형은 종속변수의 클래스가 2개인 경우를 이진(Binary Class) 분류문제밖에는 풀지 못한다.

이때는 OvO (One-Vs-One) 방법이나 OvR (One-vs-the-Rest) 방법 등을 이용하여 여러개의 이진 클래스 분류문제로 변환하여 푼다.

OvO 방법¶

OvO (One-Vs-One) 방법은 \(K\)개의 클래스가 존재하는 경우, 이 중 2개의 클래스 조합을 선택하여 \(K(K - 1)/2\)개의 이진 클래스 분류문제를 풀고 이진 분류문제를 풀어 가장 많은 결과가 나온 클래스를 선택하는 방법이다. 선택받은 횟수로 선택하면 횟수가 같은 경우도 나올 수 있기 때문에 각 클래스가 얻은 조건부 확률값을 모두 더한 값을 비교하여 가장 큰 조건부 확률 총합을 가진 클래스를 선택한다.

OvR 방법¶

OvO 방법은 클래스의 수가 많아지면 실행해야 할 이진 분류문제의 수가 너무 많아진다.

OvR(One-vs-the-Rest) 방법은 \(K\)개의 클래스가 존재하는 경우, 각각의 클래스에 대해 표본이 속하는지(y=1) 속하지 않는지(y=0)의 이진 분류문제를 푼다. OvO와 달리 클래스 수만큼의 이진 분류문제를 풀면 된다.

OvR에서도 판별 결과의 수가 같은 동점 문제가 발생할 수가 있기 때문에 각 클래스가 얻은 조건부 확률값을 더해서 이 값이 가장 큰 클래스를 선택한다.

데이터 사이언스 스쿨